問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）①
－８＋５＝－３
②
１＋３×（－２/７）
＝１－６/７＝１/７
③
２（ａ＋４ｂ）＋３（ａ－２ｂ）
＝２ａ＋８ｂ＋３ａ－６ｂ
＝５ａ＋２ｂ
④
√27－６/√３
＝３√３－２√３
＝√３
⑤
（ｘ＋１）2＋（ｘ－４）（ｘ＋２）
＝ｘ2＋２ｘ＋１＋ｘ2－２ｘ－８
＝２ｘ2－７
（２）
９ｘ2－４ｘ2
＝（３ｘ＋２ｙ）（３ｘ－２ｙ）
（３）
10－ｎが平方数となれば根号が外れる。
ｎが自然数なので、√（10－ｎ）は√１、√４、√９しかない。
10－ｎ＝１ ➡ ｎ＝９
10－ｎ＝４ ➡ ｎ＝６
10－ｎ＝９ ➡ ｎ＝１
ｎ＝１、６、９
（４）
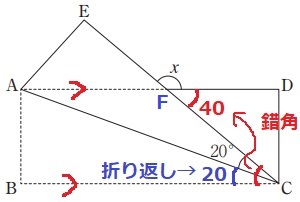
折り返しで∠ＡＣＢ＝20°
錯角で∠ＦＣＢ＝∠ＣＦＤ＝40°
ｘ＝180－40＝140°
（５）
花子が和夫より３大きい目を出す。
（和、花）＝（１、４～６）（２、５～６）（３、６）
計６通り
６/36＝１/６
大問２（小問集合２）
（１）
底面の円の半径は３ｃｍ
高さは立面図の半分で三平方→√（６2－３2）＝３√３ｃｍ
３×３×π×３√３÷３＝９√３πｃｍ3
（２）
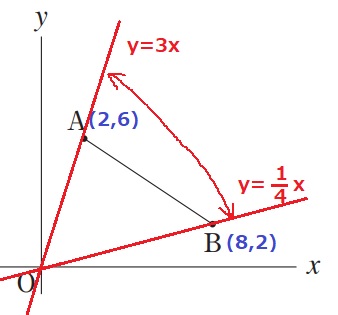
↑この範囲にあればＡＢ上を通る。
１/４≦ａ≦３
ア…１/４、イ…３
（３）①
ア：階級の幅は共に２。〇
イ：最頻値（モード）は４月が３冊、５月が７冊。×
ウ：30人の中央値（メジアン）は15番目と16番目の平均。４月が３冊、５月が７冊。〇
エ：４月は８/30（≒0.27）、５月は７/30（≒0.23）。×
オ：４月は25人、５月は13人。×６冊以上を数えても良い。
ア・ウ
②
階級値で計算する。
（１×３＋３×３＋５×７＋７×10＋９×７）÷30
＝180÷30＝６冊
（４）
連立の題材がおもしろい(*‘ω‘ *)
答案では過程も記述する。
先月の公園清掃ボランティアをｘ、先月の駅前清掃ボランティアをｙとする。
右側の文章から、ｙ－ｘ＝30…①
左側の割合を使う。50％増→1.5倍に変換。
1.5ｘ＋1.2ｙ＝1.3（ｘ＋ｙ）…②
②を10倍して整理すると、、
15ｘ＋12ｙ＝13ｘ＋13ｙ
２ｘ＝ｙ…③
これを①のｙに放り込み。
２ｘ－ｘ＝30
ｘ＝30
③に放り込んで、ｙ＝30×２＝60
先月の公園清掃ボランティアは30人、先月の駅前清掃ボランティアは60人。
大問３（規則）
（１）①
↑右側からみるとこんな感じ。
左上だけが３面。左上以外の一番上の辺と一番左の辺が２面。
右下の正方形が１面。
ア…（５－１）×２＝８
イ…６2＝36
②
（８－１）2＝49個
③
１辺がｎの正方形に１を足す。
２ｎ＋１個
（２）①
３番目の３×３の正方形では、１＋２＝３個移動。
４番目の４×４の正方形では、１＋２＋３＝６個移動。
６番目の６×６の正方形では、１～５の総和で15個。
②
答案では過程も記述する。
ｘ番目の箱の個数は、１辺がｘ個の正方形だからｘ2個。
表２より、見えない箱はｘ－１個。
（箱の個数）－（見えない箱）＝（見えている箱）
ｘ2－（ｘ－１）＝111
ｘ2－ｘ－110
＝（ｘ－11）（ｘ＋10）＝０
ｘ＞０なので、ｘ＝11
大問４（関数）
（１）
変域問題。原点０を通過する点に注意！。
ｘ＝－６のとき、最小値ｙ＝－９
ｘ＝０のとき、最大値ｙ＝０
－９≦ｙ≦０
（２）
見落としやすい(´Д`||)
１つはＰＡ＝ＰＢ。
もう１つはＡＰ＝ＡＢとＢＰ＝ＢＡだが、こちらは２通りずつある。
計５個。
（３）
ｙ＝－１/４ｘ2にｘ＝－２を放り込んで、Ｃ（－２、－１）
ＣとＡ（４、－４）を通る直線の式を考える。
Ｃ→Ａに移動すると右に６、下に３だから、傾きは－３/６＝－１/２
Ｃから左に２、上に１移動してＰ（－４、０）
（４）
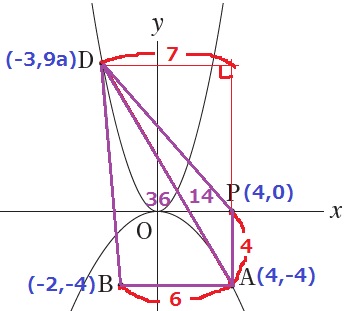
座標を確認。ｙ＝ａｘ2にｘ＝－３を代入してＤ（－３、９ａ）
四角形ＰＡＢＤをＡＤで分割。
△ＡＤＰの面積…４×７÷２＝14
△ＡＢＤの面積…50－14＝36
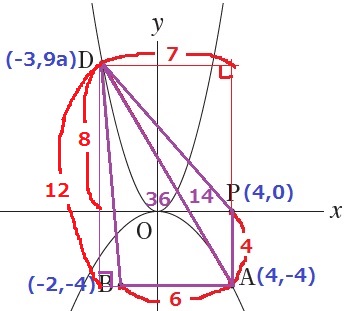
△ＡＢＤの高さ…36×２÷６＝12
Ｄのｙ座標（９ａ）…12－４＝８
９ａ＝８
ａ＝８/９
大問５（平面図形）
（１）
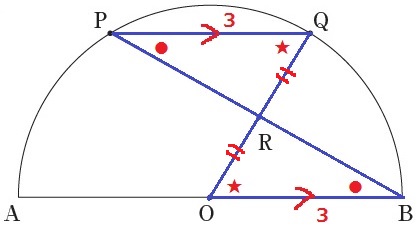
ＰＱ//ＡＢから２つの錯角＋３ｃｍの等辺＝一辺両端角相等→△ＰＱＲ≡ＢＯＲ
ＯＲ＝ＱＲ
ＱＲ＝３÷２＝３/２ｃｍ
（２）
円周角定理で、∠ＢＯＱ＝36×２＝72°
３×３×π×72/360＝９/５πｃｍ2
（３）①
△ＲＱＳ∽△ＲＰＱの証明。
辺の情報が乏しいので角度攻め。
共通角があるので、もう１つはどちらの角度か。
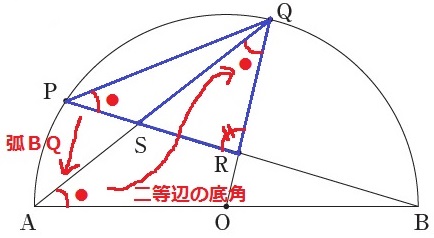
弧ＢＱの円周角で、∠ＲＰＱ（●）＝∠ＯＡＱ（●）
半径から△ＯＡＱが二等辺。
その底角で∠ＯＡＱ（●）＝∠ＲＱＳ（●）
２角が等しく∽。
②
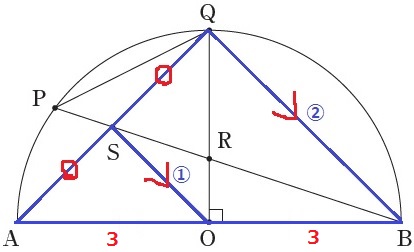
ＳＯ//ＱＢで２角が等しい→△ＡＳＯ∽△ＡＱＢ
ＡＳ：ＳＱ＝ＡＯ：ＯＢ＝１：１
相似比（もしくは中点連結定理）からＳＯ：ＱＢ＝①：②
同様に、平行線から△ＯＳＲ∽△ＱＢＲで、
辺の比からＯＲ：ＲＱ＝①：②
ＯＲ＝３×①/③＝１ｃｍ
△ＯＲＢで三平方→ＢＲ＝√10ｃｍ
大問１
（４）このレベルの角度は小学校の算数でもでるよ！
（５）花子がどんな目を出せば和夫より上に行けるか。
大問２
（４）変化球のある出題で戸惑いがち。正答率は高くなさげ。
大問３
規則はそんなに複雑ではなかった。
大問４
（２）３個見つけて安心する人が多そう。
（４）ＢＡ⊥ＡＰでＢＡとＡＰの長さが分かってるので、四角形をＤＡで分割。
大問５
（３）②最後のわりには素直であった。
ＢＲを１辺とする直角三角形は△ＯＲＢ。
ＯＢ＝３がわかっているからＯＲを知りたい。
ＯＲを１辺とする三角形は…とゴールから逆算して解法を編み出す。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
