2020年度　豊島岡女子学園中学過去問【理科】大問１解説

問題ＰＤＦ
　自然の長さが10ｃｍで重さの無視できるばねを天井につるしておもりを取りつけるとばねは伸び、ばねを床に取りつけておもりをのせるとばねは縮みます。このばねの長さとおもりの重さの関係は、グラフのようになります。

（１）
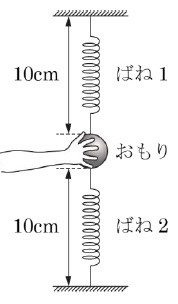
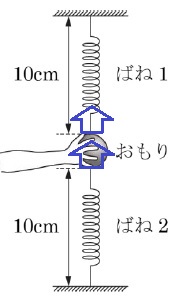
このばねを２つ用意し、40ｇのおもりの上下に取りつけました。上側のばね１の端を天井に、下側のばね２の端を床に取りつけ、ばね１、ばね２の長さがそれぞれ10ｃｍになるようにおもりを手で支えました。ばね１、おもり、ばね２は一直線上にある状態になっていました。おもりを静かにはなしてしばらく待つと、ばね１、おもり、ばね２は一直線上にある状態で静止しました。このとき、ばね１とばね２の長さはそれぞれ何ｃｍになりますか。四捨五入して整数で求めなさい。

　ばねの代わりに、自然の長さが10ｃｍで重さの無視できるゴムひもを用いると、ゴムひもはばねと同じように伸びますが、縮めようとしてもたるんでしまうため、ゴムひもは10ｃｍの長さのままです。ゴムひもの長さとおもりの重さの関係は、グラフのようになります。

（２）
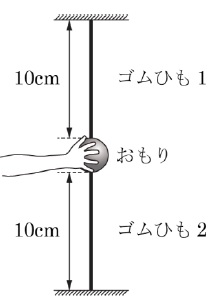
このゴムひもを２つ用意し、（１）のばね１、２の代わりにゴムひも１、２を取りつけました。おもりを静かにはなして止まるまで待つと、ゴムひも１とゴムひも２の長さはそれぞれ何ｃｍになりますか。四捨五入して整数で求めなさい。

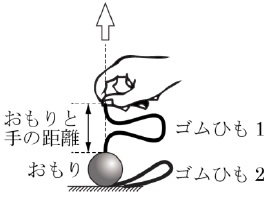
　ゴムひも１の端を天井からはずして手で持ち、ゴムひも１とゴムひも２をたるんだ状態にして、おもりを床に置きました。はじめにおもりと手の距離を０ｃｍとしてから、ゴムひも１を持つ手をおもりの真上に向けて一定の速さでゆっくりと動かし、ゴムひもの合計の長さが30ｃｍになるまで引っ張りました。

（３）
手を動かし始めてから時間を横軸に、ゴムひも１とゴムひも２の長さを縦軸にとったグラフとして正しいものをそれぞれ１つずつ選びなさい。

　次に、下の図のように、太さが均一な40ｇの棒の左端をばねばかりで、右端をゴムひもでつるし、水平になるようにしました。ばねはかりは１ｋｇまではかることができます。棒のちょうど中央におもりをつるせるようになっていて、中央におもりをつるしたときに、ゴムひもがどれだけ伸びるか調べる実験をしました。

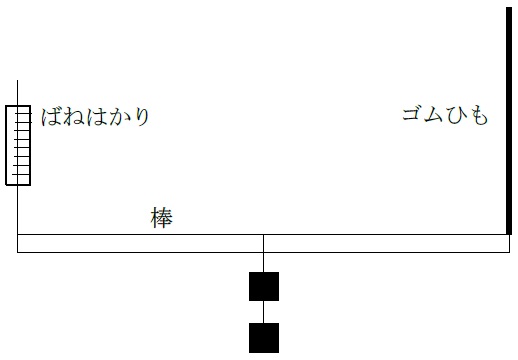
棒の中央に100ｇのおもりを１個ずつ増やしていった場合について、ゴムひもの長さを測定しました。その結果は、下の表のようになりました。

（４）
おもりの重さが200ｇのとき、ばねはかりの目盛りは何ｇを指していますか。
四捨五入して整数で求めなさい。

（５）
今度は、100ｇのおもりを何個かゴムひもに直接つるしました。これまでの実験結果から、おもりの個数とゴムひもの伸びの比が変わらない（おもりの個数とゴムひもの伸びが比例している）のは、おもりが何個のときまでと考えられますか。

ばねは伸びたら縮もうとし、縮んだら伸びようとする。
もとの自然長に戻ろうとする力を弾性力という。
弾性力でばね１はおもりを上にあげ、ばね２は下から押す。
２つのばねは同じばねで、グラフから縮んだときと伸びたときののびの大きさは同じだから、
40÷２＝20ｇずつ均等にかかっている。
ばね１は２ｃｍ伸びて12ｃｍ、ばね２は２ｃｍ縮んで８ｃｍ。

（２）ゴムひも１…14ｃｍ、ゴムひも２…10ｃｍ
一方で、ゴムひもは伸びるときに弾性力が働くが、たるんだときは弾性力が働かない。
ゴムひも１に40ｇがかかるので長さは14ｃｍ。
ゴムひも２はたるんだ状態で、たるんでいるときの長さはグラフから10ｃｍ。

（３）ゴムひも１…か、ゴムひも２…お
横軸の時間が詳しく記載されていないので変化に注意する。
はじめ、ゴムひも１はたるんでいる状態で10ｃｍのまま。
10ｃｍを超えると、おもりの重さは地面だけでなくゴムひも１にもかかって伸びる。
ゴムひも１が14ｃｍ伸びておもりが地面から離れると、ゴムひも１に40ｇすべてがかかる。
24ｃｍを超えるとゴムひも２が伸びて下からひっぱり、ゴムひも１が上からひっぱり伸びる。
このとき、手に引っ張られて変形する伸び率は１と２で半分ずつ。

（４）120ｇ
均一な棒なので、棒の重さ40ｇはおもりが吊るされる真ん中にかかる。
ばねはかりにかかる重さは、（200＋40）÷２＝120ｇ

（５）３個
表の最初のほうでは100ｇで５ｃｍずつ伸びているが、
600ｇ→700ｇで６ｃｍ伸びている。
おもりが600ｇのとき、ゴムひもにかかる力は（600＋40）÷２＝320ｇ
700ｇでは、（700＋40）÷２＝370ｇ
320～370ｇのどこかで比例関係が崩れる。
おもりの重さの合計は100の倍数なので、おもり３個まで比例関係がつづく。
*元に戻らなくなる限界値を弾性限界という。
難関中学（理科）解説ページに戻る