問題PDF
(1)
すべての位の数字が1である数を、A(1)=1、A(2)=11、A(3)=111…
のように、1の個数を使って表すことにします。これらの数の中で
(あ)9の倍数となるものを1つ求め、記号Aを使って表しなさい。
(い)33の倍数となるものを1つ求め、記号Aを使って表しなさい。
(う)13の倍数となるものを1つ求め、記号Aを使って表しなさい。
(2)
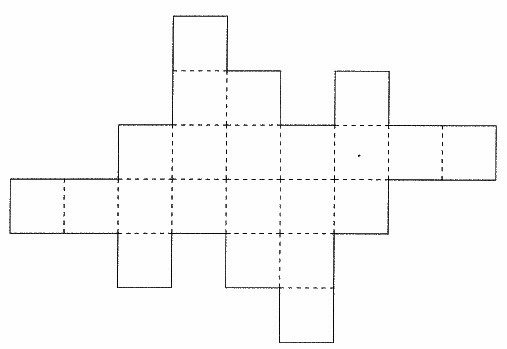
次の図は1辺5cmの正方形をつなぎ合わせた図形です。
これを、どの正方形も重なることなくうまく組み立てると、体積の異なる2種類の直方体が作れます。
それぞれの直方体の体積を求めなさい。ただし、点線以外で折ってはいけないこととします。
(3)

@解説@
(1)(あ)
位の和が9の倍数であれば、その数は9の倍数。
1を9の倍数個並べる。A(9)、A(18)、A(27)…どれも正解。
(い)
33の倍数=11の倍数×3の倍数
すべての位が1である数なので、1が偶数個並べば11の倍数。
また、位の和が3の倍数であれば、その数は3の倍数→1を3の倍数個並べる。
つまり、偶数個(2の倍数個)かつ3の倍数だから、1を6の倍数個並べる。
A(6)、A(12)、A(18)…どれも正解。
(う)
知識問題です。
【7×11×13=1001】
1001は有名な合成数なので覚えておこう。
1001の倍数は13の倍数。
筆算で1001×111をすると111111となるので、A(6)
(2)

これを頭のなかで組み立てるのは無理ゲー(;`ω´)
真ん中に正方形がくっつくところが多いので、そこらへんが底辺になると思われる。
面の数を数えてみると22面ある。
もし、縦・横・高さいずれにも2つの正方形が並ぶと、2×2×6=24面使われる。
これより面の数が少ないということは、どこかの辺は正方形1つ分。
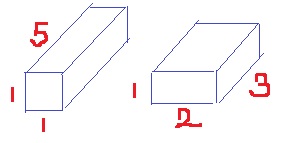
高さを正方形1つ分として、表面積が正方形22個になる組み合わせは2つしかない。
(5×5×5)×5個=625cm3
(5×5×5)×6個=750cm3

組み立て予想図の一例。
こういう問題ってどうやって作るのでしょうか??
(3)
難しい:(っ`ω´c):
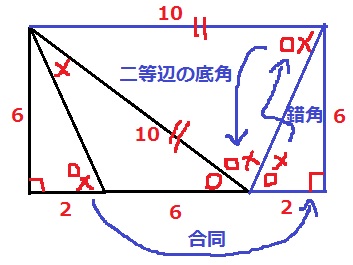
外角定理で左の直角三角形の内角の1つは〇+×。
この直角三角形と合同な図形を右側に設置して、全体を長方形にする。
すると、長方形の横が2+6+2=10cmだから、等辺10cmの二等辺三角形が現れる!
〇+×を錯角であげ、二等辺の底角で降ろす。
〇+〇+〇+×+×=180°より、〇が3個、×が2個。



コメント