問題PDF
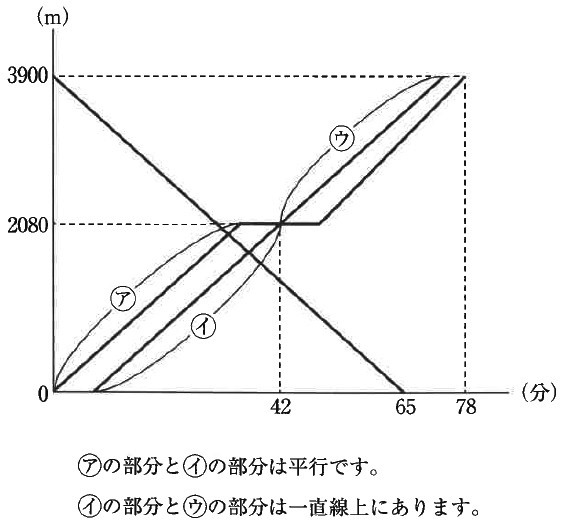
AさんとBさんは同じ道を通り、P地点から、途中のQ地点で10分間休けいをとり、R地点へ行きました。BさんはAさんより少し遅れて出発し、Aさんの8分後にR地点に着きました。Cさんは9時にAさんと同時に出発し、R地点から、AさんとBさんと同じ道を通り、休まずP地点へ行きました。下のグラフは、3人が出発してからの時間(分)と、着くまでに進んだ距離(m)をグラフに表したものです。
(1)
BさんはAさんが出発してから何分後に出発しましたか。
(2)
AさんがR地点に着いたのは何時何分後ですか。
(3)
CさんがBさんとすれちがったのは、何時何分後ですか。
ただし、秒は切り捨てて答えなさい。
(4)
もしCさんが、AさんとBさんの2人と同時に会う速さで進んでいた場合、
何時何分にP地点に着きますか。
@解説@
(1)

0mがP、2080mがQ、3900mがR。
AとCが同時に出発、遅れてBが出発。
BはAの8分後にRへ着くので、ここからAとBは上のようになる。
つまり、AがQで休憩を終えた42分後に、BがQに到着する。
アとイは平行→P-Q間のAとBは同じ速さ。
アとイを対辺とする四角形は平行四辺形。10分を下におろす。
BはAの10分後に出発したことになる。
(2)
78-8=70分
9時の70分後→10時10分
*イとウは一直線だから、アとウも平行で傾きが同じ。
Aは休憩後も休憩前の速度で歩いている。
しかし、ウを1辺とする四角形は平行四辺形でない。
BがRに着いたとき、Aから10分遅れではなく8分遅れであった。
→Bは休憩を終えてから速度をあげている。
(3)

★のところでBとCが出会う。
休憩前のBは32分で2080m歩く。
Bの速さは、2080÷32=分速65m
Cは65分で3900m歩く。
Cの速さは、3900÷65=分速60m
速さの比は、B:C=65:60=⑬:⑫
時間の比は逆比。B:C=【12】:【13】
これをグラフで表すと、下の青い三角形の底辺の比になる。
55分=【25】だから、★の時間は、10+55×12/25=36.4≒36分
9時36分
(4)

AとBは★で出会うので、Cがそこを通る線を描く。
青線の三角形で相似。
42×3900/1820=90分
9時から90分後→10時30分



コメント