2019年度　浦和明の星女子中学過去問【算数】大問１解説

問題ＰＤＦ
（１）

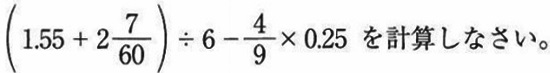
（２）
下の図は、正方形を４つの長方形Ａ、Ｂ、Ｃ、Ｄに分けたもので、
長方形Ａの面積が３ｃｍ²、Ｂの面積が９ｃｍ²、Ｃの面積が６ｃｍ²です。
正方形Ｄの周り（太線部分）の長さを答えなさい。

（３）
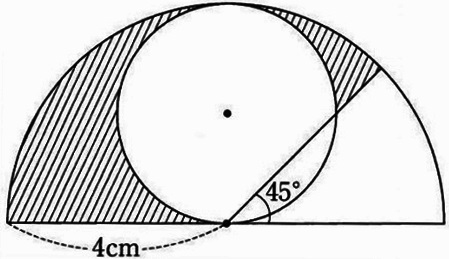
下の図は、大きな半円と小さな半円と直線を組み合わせたものです。
図の斜線部分の面積を求めなさい。

（４）
ある果樹園では、桃と梨を栽培しています。
昨年の収穫は、桃と梨の個数の比が５：８でした。
今年の収穫は、昨年よりも桃の個数が160個増えて梨の個数が30個減り、
桃と梨の個数の合計では１割増えました。
昨年は何個の桃を収穫しましたか。

（５）
学校の花壇に植えるために、アサガオの苗を何本か用意しました。
花壇の左端から10ｃｍ離れた所に１本目を植え、その後10ｃｍずつ間をあけて植えると、
花壇の右端の２ｍ40ｃｍ手前までしか植えられません。
また、花壇の左端から15ｃｍ離れた所に１本目を植え、その後15ｃｍずつ間をあけて植えると、
花壇の右端の15ｃｍまで植えられますが、苗は１本残ります。
苗は何本用意しましたか。

（６）
１から９までの整数を書いたカードが１枚ずつあります。
このうち５枚のカードを選んで円形に並べ、隣り合った２枚のカードに書いてある整数の差を
これら２枚のカードの間に書くことを、２回行いました。
１回目は図１のようになりました。
２回目は図２のようになり、整数Ａ、Ｂ、Ｃ、Ｄ，Ｅの合計は２１になりました。
Ａ，Ｂ、Ｃ、Ｄ、Ｅを答えなさい。

（７）
あるクラスで、紙テープを折りたたんで正五角形の飾りを作ることになりました。
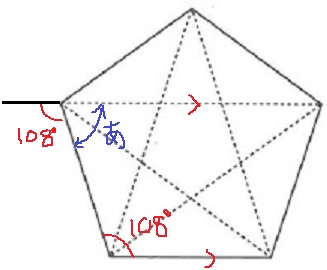
先生は、下の図のように、点線を折り目として折りたたんだときに正五角形の飾りができるように紙テープを切っておきました。

（ア）【あ】の角度は何度ですか。
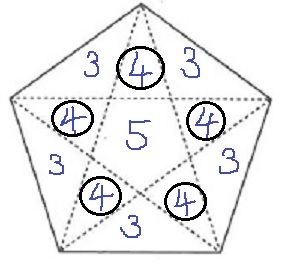
（イ）できた正五角形の飾りには、紙テープが４枚重なっている部分があります。
その部分を解答欄にある正五角形を黒く塗って示しなさい。

（１）

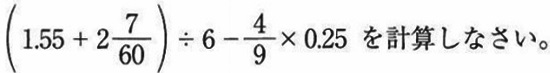
＝（１・11/20＋２・7/60）÷６－４/９×１/４
＝220/60×１/６－１/９
＝（220－40）/360＝180/360＝１/２

（２）
慣れていないと案外、ドツボにはまりやすい。

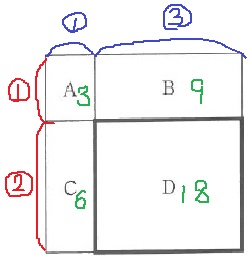
四角形の面積比を使う。横の辺が１：３。縦の辺が１：２
ここから、Ｄが１８ｃｍ²とわかる。
４つの長方形をたすと３６ｃｍ²→正方形の１辺は６ｃｍ
③＝６×３/４＝4.5ｃｍ、②＝６×２/３＝４ｃｍ
（4.5＋４）×２＝１７ｃｍ

（３）

この区切り方がわかりやすいかな？
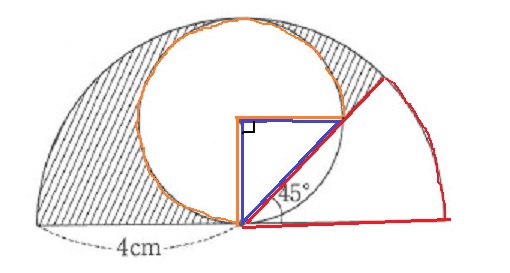
中心角135°の扇形から、270°の扇形（緑）と直角二等辺（青）を引く。
４×４×3.14×135/360－２×２×3.14×270/360－２×２÷２＝
＝（６－３）×3.14－２＝7.42ｃｍ²

（４）
昨年の桃の個数を⑤、梨を⑧とおく。合計は⑬。
この１割は、⑬×１割＝○1.3
桃160個増えて、梨30個減った→合計で130個増えた。
○1.3＝１３０なので、
130×⑤/○1.3＝５００個

（５）
植木算っぽいが、実態は差集め算。

花壇の右端との距離を考える。
１0ｃｍずつだと240ｃｍ手前で終わる。
１５ｃｍずつだと花壇の右端に最後の苗がくる（強引にすべて植える）。
240ｃｍの差は、５ｃｍずつの差の集まり。
２４０÷５＝４８本

（６）
推論問題。

図１は例題。図２を考える。差だけで、どちらが大きい数かはわからない。
ＡとＥの差が８なので、【Ａ・Ｅ】は１か９
２通りで試してみる。

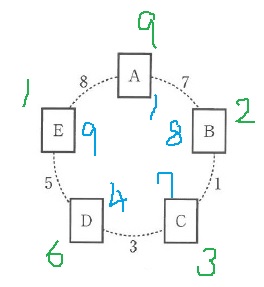
合計が21となるのは、外側の組み合わせ。
Ａ…９、Ｂ…２、Ｃ…３、Ｄ…６、Ｅ…１

（７）①

正五角形の内角の１つが108°。
錯角で上げて、180－108＝７２°

②

４のところが正解。
コツは、台形の上底か下底を見ること。
短い方が正五角形の１辺、長い方が中の星の１辺。
難関中（算数科）解説ページに戻る