図１のように、１辺の長さが１ｃｍの正方形のタイルに半径が１ｃｍの円の一部が描かれているものがたくさんあります。また、１辺の長さが１ｃｍの正方形９つに区切られた図２のようなパネルがあり、このタイルをはめることができます。
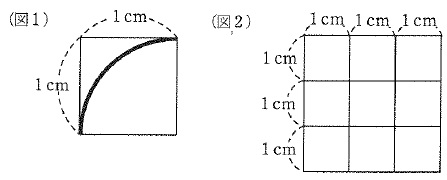
タイルのうちいくつかをパネルにはめこみ、輪を作ります。ただし、輪とは、ある点から始めて、同じ点を通ることなく、すべての点を通って元の点に戻ることのできる形のこととします。例えば、図３と図４の２つの形は輪ですが、図５と図６の２つの形は輪ではありません。
（１）
輪に囲まれた部分の面積がもっとも大きくなるのは、輪がどのような形のときですか。
解答用紙のパネルに輪を書きこみなさい。
（考えられるものがいくつかあるときはそのうちの１つでかまいません）
（２）
輪に囲まれた部分の面積として考えられるものは何通りありますか。
（３）
輪に囲まれた部分の面積が図４のときと同じになるような輪の形は、
図４の場合を含めて全部で何通りありますか。
ただし、回転や裏返しでちょうど重なるものは同じとします。例えば、
の２種類は回転や裏返しで図４の輪と重なるので、すべて同じものとします。
＠解説＠
*入試では（２）と（３）は考え方も記述する。
（１）
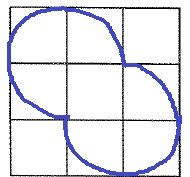
↑面積を最大にするので、外側への膨らみを意識する。
（２）
まず、２×２の正方形だけで考える。
基本形を円とすると、４つの弧のうち、いくつを欠けさせるか。
５通り
今度は、３×３の正方形で考える。
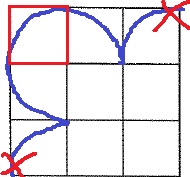
左上の正方形から始めて、大きな正方形の隣にある頂点に移動しようとすると輪にならない。
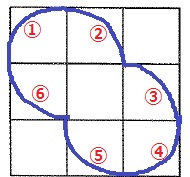
結局、前問の解答が基本形になる|д･)
６つの弧のうち、いくつの弧を欠けさせるか→７通り
この７通りは真ん中に１ｃｍ2の正方形があり、先ほどの５通りと面積がかぶらない。
よって、12通り。
（３）
これも（１）を基本形とする。図４は①と⑥の弧が欠けた状態。
上下・左右対称移動して重複しない組み合わせを調べる。
６通り。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント