問題ＰＤＦ
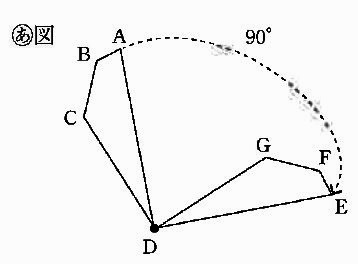
四角形ＡＢＣＤを、（あ）図のように矢印の向きに回転させ、四角形ＥＦＧＤと重ねるように動かすことを、「四角形ＡＢＣＤを点Ｄのまわりに、時計まわりに90°回転させる」といいます。
次のア、イ、ウにあてはまる数をそれぞれ求めなさい。
（１）
（い）図は、ある四角形を点Ｏのまわりに、時計まわりに90°回転させるとき、その四角形が通るところを表したものです。曲線ＰＲは点Ｏを中心とする円の一部です。３つの点Ｑ、Ｏ、Ｒは一直線上にならんでいます。また、直線ＰＱの長さと直線ＱＯの長さは等しいです。この四角形の角のうち、最も小さい角の大きさは〔 ア 〕°です。
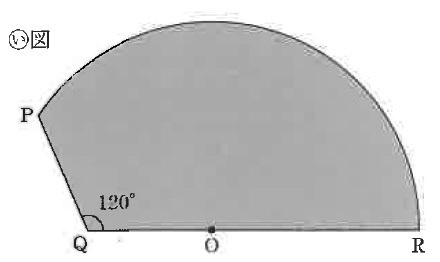
（２）
（い）図は、（１）とは別の四角形を点Ｏのまわりに時計まわりに（ ）°回転させたとき、その四角形が通ったところを表したものと考えることもできます。（ ）にあてはまる数のうち、最も小さいものは〔 イ 〕°で、そのときの四角形の角のうち、最も小さい角の大きさは〔 ウ 〕°です。
＠解説＠
（１）
回転させた図形の軌跡ではなく、軌跡から回転させた図形を求める。
四角形の頂点のうち、Ｏ・Ｐ・Ｑは確定している。
残る頂点をＳとし、Ｓが弧ＰＲ上のどこにくるかを判定する。
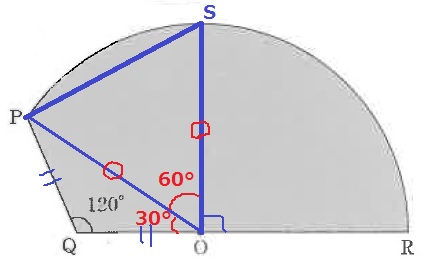
90°回転させるので、∠ＳＯＲ＝90°
ＳはＯの真上にくる。
ＰＯに補助線、△ＰＱＯは二等辺なので、
∠ＰＯＱ＝（180－120）÷２＝30°
△ＰＳＯは頂角を60°とする二等辺三角形→すなわち、正三角形。
四角形ＰＱＯＳの角のうち、最も小さい∠ＰＳＯ＝60°
（２）
回転させる角度を最小にする。
残りの頂点をＴとしたとき、Ｔは弧ＰＲ上のどこにくるか。
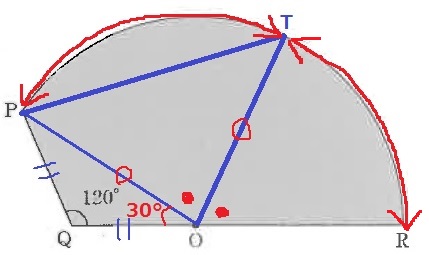
配慮すべきは弧ＰＲ。
ＴがＲに近づくほど、回転させるべき角度は小さくなるが、
あまり近づけすぎるとＰの移動距離が短くなり、Ｔの左側が開いてしまう。
そこで、ＰとＲの真ん中（∠ＰＯＲの二等分線上）にＴを配置する。
回転すべき角度→∠ＴＯＲ＝（180－30）÷２＝75°
△ＯＰＴは二等辺。
四角形ＰＱＯＴの角のうち、最も小さい∠ＰＴＯ＝（180－75）÷２＝52.5°
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント