問題ＰＤＦ
Ａさん、Ｂさん、Ｃさんの３人は同時にＳ地点をスタートし、
Ｇ地点にゴールするまでの40ｋｍのマラソンコースを次のように走りました。
Ａさん：Ｓ地点からＧ地点まで一定の速さで走りました。
Ｂさん：Ｓ地点から20ｋｍ地点まで一定の速さで走り、
20ｋｍ地点からＧ地点までは速度を落として一定の速さで走りました。
Ｃさん：Ｓ地点から【Ｘ】ｋｍ地点までは一定の速さで走り、
【Ｘ】ｋｍからＧ地点までは速度を上げて一定の速さで走りました。
その結果、10ｋｍごとの順位と前走者との差は下の表のようになりました。
例えば10ｋｍ地点では、１番にＢさんが通過し、その２分後にＡさんが通過し、
さらにその２分後にＣさんが通過しました。次の問いに答えなさい。
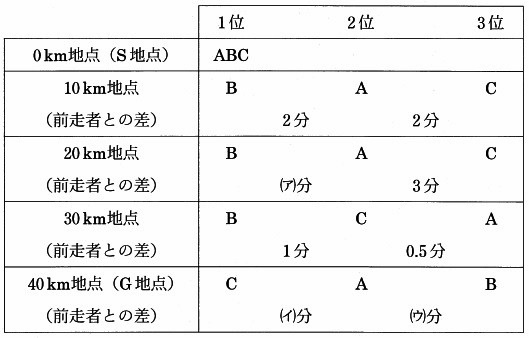
（１）
アに当てはまる数を答えなさい。
（２）
下のグラフは、Ｃさんのスタートしてからゴールするまでの時間と
Ｓ地点からの距離の関係を表したものです。正しいものを選びなさい。
（３）
イ・ウに当てはまる数を答えなさい。
（４）
ＣさんがＡさんに追いついたのはＳ地点から何ｋｍの地点ですか。
（５）
【Ｘ】に当てはまる数を答えなさい。
（６）
Ｃさんの20ｋｍ地点からＧ地点までかかった時間は、
Ｓ地点から20ｋｍ地点までかかった時間の0.9倍でした。
ＣさんはＳ地点からＧ地点まで何分で走りましたか。
＠解説＠
むづかしい:;(∩´＿`∩);:
各々の速さと、どこからどこまでかかった時間が不明。
（１）
わかっているのは、10ｋｍ地点ごとにおける他者との時間差。
Ｂは20ｋｍまで速さは一定。
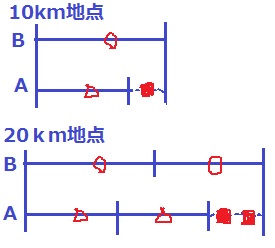
２人の速さがわからなくても、速さが一定であれば距離と時間は比例。
距離が２倍になれば、時間も２倍になる。時間の差も２倍になる。
10ｋｍ地点でＢとＡの差は２分だったので、20ｋｍ地点では４分。
ア…４
（２）
10ｋｍ地点ではＡがＣより２分先に着いた。
20ｋｍ地点ではＡがＣより４分先に着くところ、３分になっている。
ということは、Ｃが速度を変えたのは10～20ｋｍ地点のあいだとなる。
③
（３）
先にウから。
Ｂは20ｋｍ地点で速度を落とし、その後の速さは一定。
20ｋｍ地点でＢはＡに４分差であったが、30ｋｍ地点で1.5分の差となり、
４－1.5＝2.5分、差が縮まっている。
40ｋｍ地点でも2.5分差で縮まるので、2.5－1.5分＝１分、ＡがＢより先に着く。
ウ…１
イも同様。
Ｃは20ｋｍ以降は速さが一定。
20ｋｍ地点でＡがＣより３分早かったが、30ｋｍ地点ではＣがＡより0.5分早く着いた。
時間の差は、３＋0.5＝3.5分縮まった。
よって、40ｋｍ地点では、0.5＋3.5＝４分先にＣが着く。
イ…４
（４）
ここらへんから、きつくなってくる。
本問以降でＢは使わないので、ＡとＣだけで考える。
ＡとＣは10ｋｍ地点ごとの時間差しかわかっていない。
ＡとＣの順位が逆転するのは20～30ｋｍの範囲内にある。
Ａが20ｋｍ地点についたとき、その３分後にＣが20ｋｍ地点につく。
どこかでＣが追いつき、Ｃの到着から0.5分後にＡが30ｋｍ地点につく。
ＡとＣの速さは一定で、青と赤の矢印はそれぞれ走った時間が同じ。
ＣはＡに追いつく前は３分、追いついた後は0.5分の時間をＡより多く歩いている。
この時間の差が追いつく前後の距離の比にあたる。
３：0.5＝６：１
20＋10×６/７＝200/７ｋｍ
＠別解＠
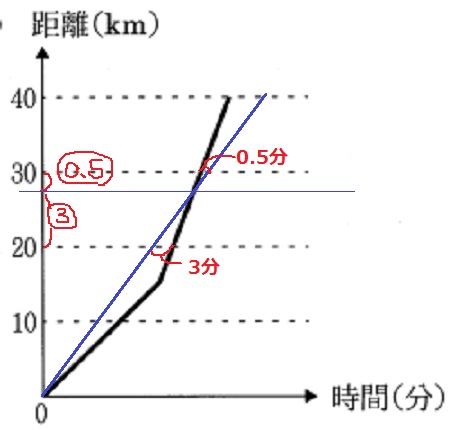
グラフだと視覚的にわかりやすい。
２つの三角形の相似から、３：0.5＝６：１となる。
（５）
きつい(´ﾟдﾟ｀)
時間差をうまく使う。
ＡとＣが同じ距離（10ｋｍ）を走ると、
Ｃが速さを変える前は、ＡがＣより２分早い。
Ｃが速さを変えた後は、ＣがＡより3.５分早い。
↑青線はＡ
変速前と変速後の速さは、２：3.5＝④：⑦
０～変速まで④ずつＡが先に行き、開いた差を変速後に⑦ずつＣが埋めて０にする。
時間の比は逆比で、変速前：変速後＝７：４となる。
△を時間とすると…④×△７（ひらいた差）＝⑦×△４（縮めた差）
一方、Ａの速さは一定で、時間と距離は比例。
すなわち、距離の比は７：４。
200/７×７/11＝200/11ｋｍ
距離と時間と速さと時間の差と、関係性がごっちゃになりやすい。
（６）
最後まで悩みました。。:;(∩´＿`∩);:
一応、解けたのですが、文字式を使っていないにせよ、
負の数と移項を使ってしまったのが気がかりなところ。
グラフを活用する。
Ｃは、０～20ｋｍまで□10、20～40ｋｍまで□９の時間がかかった。
Ａは20ｋｍ地点までに、□10－３分かかったことになる。
20ｋｍは全体の半分だから、Ａがゴールした時間は、
（□10－３）×２＝□20－６分
Ｃの到着時刻は、□20－６－４＝□20－10分
これが□19に相当する。
□20－10＝□19
□１＝10分
□19＝190分
*別解を思いついた方は、ぜひお問い合わせの方よりご教示くださいませ。
難関中 （算数科）解説ページに戻る
コメント