問題PDF
図のような、正六角形ABCDEFがあり、その面積は10cm2です。
BG=EHでGI:IC=2:3です。次の問に答えなさい。
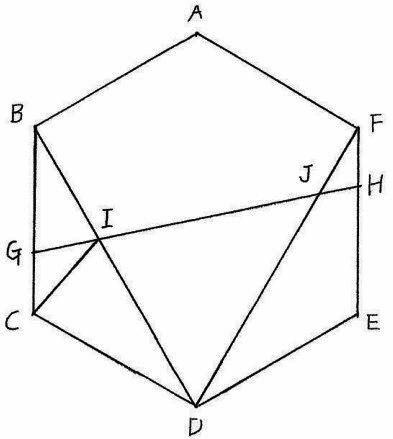
(1)
四角形ABDFの面積を求めなさい。
(2)
三角形BGIの面積を求めなさい。
(3)
三角形IDJの面積を求めなさい。
@解説@
(1)
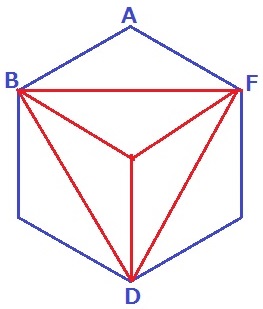
おなじみの6分割。
10×4/6=20/3cm2
(2)
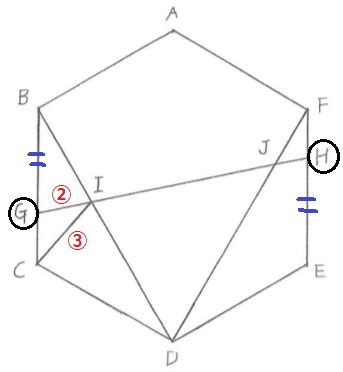
奇妙な等辺が気になる。
六角形の頂点であるB・Eが対称的な位置にあるので、
そこから等距離にあるG・Hも同様に対称性がある。
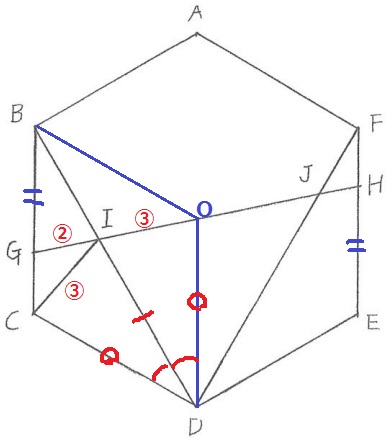
正六角形の重心をOとすると、GHはOを通過する。
△CDIと△ODIに注目。
前問の分割にでてきた、二等辺BCDと二等辺BODは合同。
CD=OD、∠CDI=∠ODI
共通辺IDを合わせ、2辺とあいだの角が等しく、△CDIと△ODIは合同。
CI=OI=③
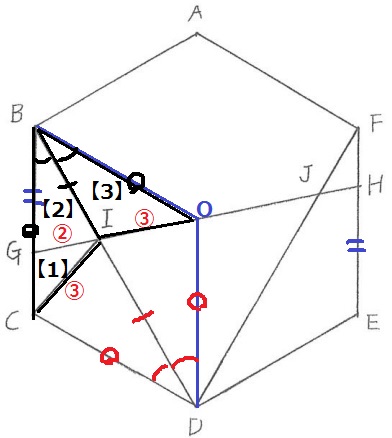
GI:IOの辺の比から、△BGIの面積を【2】とすると、△BIOの面積は【3】
△BCIと△BOIも2辺とあいだの角が等しく合同。
△BCI=【3】
△GCI=【3】-【2】=【1】
BG:GC=2:1
△BCO(正六角形の6分の1)→△BCI→△BGI
10×1/6×2/5×2/3=4/9cm2
(3)
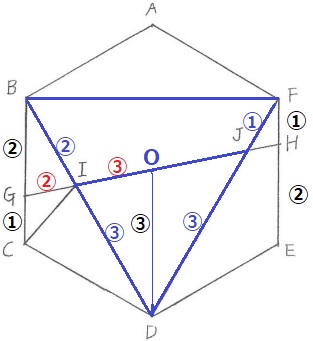
△BGIと△DOIは相似→BI:ID=②:③
△FHJと△DOJも相似→FJ:JD=①:③
△BDFは正六角形の半分で、△IDJは隣辺比で対処する。
10×1/2×(③×③)/(⑤×④)=9/4cm2



コメント