問題ＰＤＦ
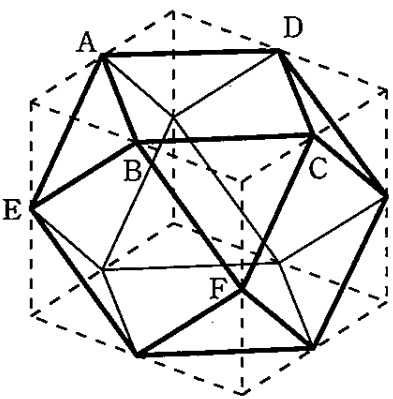
図のような、立方体の各辺の真ん中の点を結んで出来た立体Ｘがあります。
（１）
辺ＢＥの真ん中の点Ｍを通り、面ＡＢＣＤに平行な平面で立体Ｘを切断するとき、
立体Ｘの断面積は面ＡＢＣＤの面積の何倍ですか。
（２）
ＢＮ：ＮＥ＝１：２となるように辺ＢＥ上に点Ｎをとります。
点Ｎを通り、面ＢＣＦに平行な平面で立体Ｘを切断するとき、
立体Ｘの断面積は面ＢＣＦの面積の何倍ですか。
＠解説＠
（１）
△ＡＢＥは斜めの面だが、上から眺めると直角二等辺三角形にみえる。
ＭはＥＢの中点で、ＡＢと平行になるように切られるので断面はＥＡの中点も通過する。
対称性でつなげていくと、断面の形は八角形である。
左下の△ＦＥＭの面積を①とする。
辺の比から△ＡＢＥ＝△ＡＢＯ＝④
五角形ＡＦＭＢＯ＝⑧－①＝⑦（等脚台形ＡＦＭＢは③）
面積比の算出は正方形ＡＥＢＯ内で決着がつく。
正方形ＡＢＣＤ：断面積（八角形）＝△ＡＢＯ：五角形ＡＦＭＢＯ＝④：⑦
断面積は面ＡＢＣＤの７/４倍。
（２）
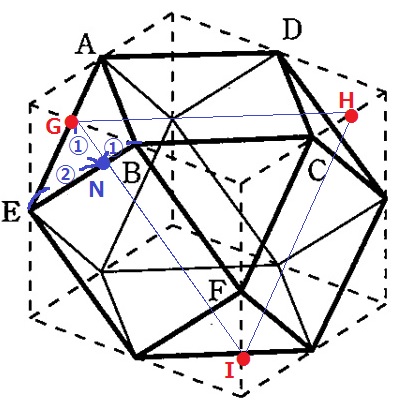
断面の作図は図形Ｘの面上ではなく、外側へ延長しよう。
ＢＦとの平行線を意識して、Ｎを通る正三角形ＧＨＩを作成。
ＥＢは右上45度線、ＧＩは右下45度線。
△ＧＢＮは直角二等辺三角形ゆえ、ＧＮ＝ＢＮ＝①
四角形ＢＮＪＦは長方形で、ＮＪ＝ＢＦ＝③
対称性からＪＩ＝ＧＮ＝①
断面積は右の赤枠のような形になる。
△ＢＣＦの面積…③×③＝【９】
断面積…⑤×⑤－①×①×３＝【22】
断面積は面ＢＣＦの22/９倍。
＠余談＠
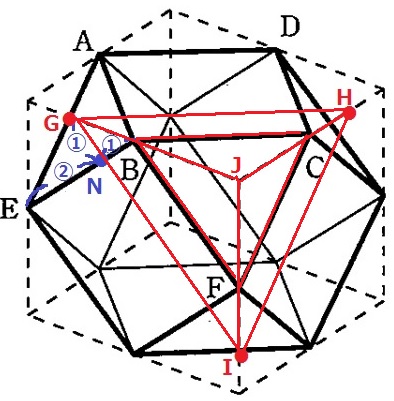
△ＢＣＦと△ＧＨＩは平行なので、三角錐Ｊ－ＢＣＦと三角錐Ｊ－ＧＨＩは相似関係にあるが、
Ｂから直接Ｇの位置を探ろうとすると失敗する(;`ω´)
ＢＪは直角二等辺三角形ＢＪＦの等辺だが、ＧＢは直角二等辺三角形ＧＢＮの斜辺にあたる。
中３で習う根号（ルート）を使わなければならない。
また、角の３つの底面は正三角形だが、立体はきれいな正三角錐ではない。
難関中（算数科）解説ページに戻る
コメント