2021年度　大阪星光学院中学過去問【算数】大問２解説

問題ＰＤＦ
下の図１のように、縦の長さが８ｃｍの長方形ＡＢＣＤがあります。

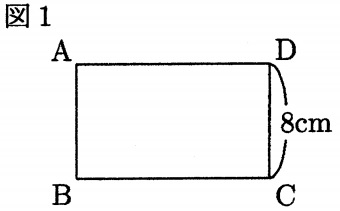
点ＰはＡを出発して辺ＡＤ上を毎秒５ｃｍの速さで何度も往復します。
また点Ｑは、点Ｐと同時にＣを出発して、辺ＣＢ上を一定の速さで何度も往復します。
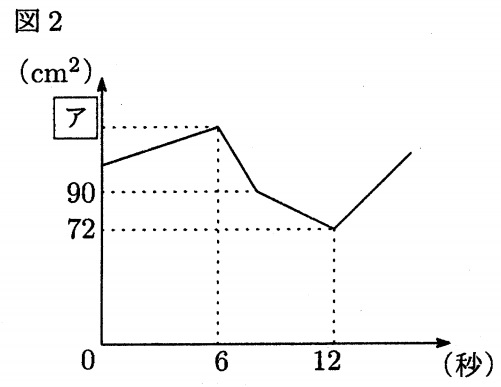
下の図２のグラフはこのときの図形ＡＢＱＰの面積の変化を表しています。

（１）
点Ｑの速さは毎秒何ｃｍですか。

（２）
図２のグラフの〔ア〕にあてはまる数は何ですか。

（３）
２点Ｐ、Ｑが出発してから180秒間で面積が最も大きくなるのは何秒後ですか。
あてはまる数をすべて答えなさい。

＠解説＠
（１）

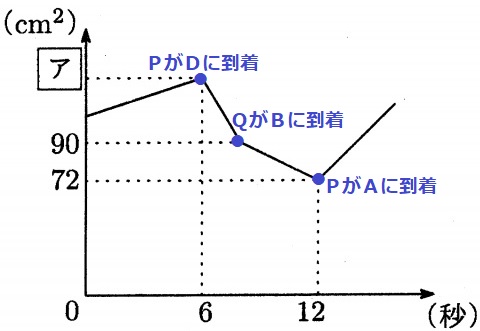
図形ＡＢＱＰの面積は、ＡＰ（上底）＋ＢＱ（下底）の和に依存する。
６秒後までは面積が増加しているのでＡＰ＋ＢＱは長くなる。
つまり、ＢＱの減少よりＡＰの増加が勝るので、ＰはＱより速いことになる。
→６秒後、先にＰがＤに到着する。
ここからグラフが急激に下がるのは、Ｐが折り返すことでＡＰとＢＱがともに短くなるから。
面積が90ｃｍ²のときにＱがＢに到着する。
６×２＝12秒後にＰがＡに戻る。

ＡＤ（長方形の横）の長さは６×５＝30ｃｍ

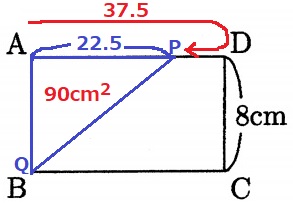
ＱがＢについたとき、ＡＰ＝90×２÷８＝22.5ｃｍ
Ｐの移動距離は、60－22.5＝37.5ｃｍ
37.5÷５＝7.5秒後
Ｑの速さは、30÷7.5＝毎秒４ｃｍ

＠別解＠

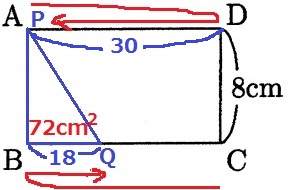
ＰがＡに戻る72ｃｍ²でも解ける。
ＢＱ＝72×２÷８＝18ｃｍ
速さの比は、Ｐ：Ｑ＝60：48＝５：４
Ｐが毎秒５ｃｍなので、Ｑは毎秒４ｃｍ。

（２）
ＡＰ＝30ｃｍ、ＢＱ＝30－４×６＝６ｃｍ
（30＋６）×８÷２＝144

（３）
図形ＡＢＱＰの面積が最大になるのは、ＰがＤ、ＱがＣにいるとき。
（長方形ＡＢＣＤと同じ面積になる）
〔ＰがＤにいる時間〕→６・18・30・42…
〔ＱがＣにいる時間〕→15・30・45…
30秒後に面積がはじめて最大化。
留意点は、はじめにＰはＡから出発しているので、
今度はＤから出発して再びＤに戻るときを考えること！
30秒後にＰはＡ→Ｄに移動するので、Ｄ→Ａ→Ｄは60秒後。
30と60の最小公倍数は言わずもがな60なので、以降60秒ごとに面積が最大化。
30＋60＝90秒後
90＋60＝150秒後
180秒間では30、90、150秒後
難関中（算数科）解説ページに戻る