問題PDF
(2)

(4)
1から7の7個の数が下の約束にしたがって左から一列に並んでいます。
いちばん左の数は他の6個の数の平均で、真ん中の数より小さいです。
また、真ん中の数より左の3個の数の和と右の3個の数の和は等しくなります。
さらに、左から2番目と右から2番目の数の和は、両はしの和に等しくなります。
①真ん中の数はいくつですか。
②この7個の数の並びを答えなさい。
(5)
〔1、2、3〕を1、2、3を並びかえてできるすべての3桁の数の和とします。
つまり、〔1、2、3〕=123+132+231+213+312+321=1332
〔3、5〕は、〔3、5〕=35+53=88
また、〔2、6、9〕ならば、〔2、6、9〕=269+296+692+629+926+962=3774です。
①〔2、4、6、8〕はいくつですか。
②〔2、4、6、8〕÷〔1、3、5、7〕を計算しなさい。
(9)
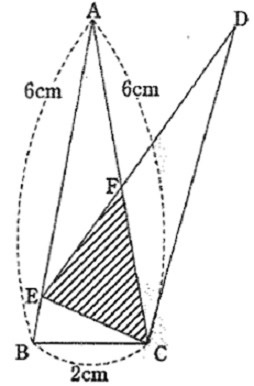
△ABCと△DECは合同です。
△CEFの面積は△ABCの面積の何倍ですか。
(10)
直方体の形をした容器に水が入っています。この容器に図1のような円柱のおもりを円の面が容器の底面につくように入れたところ、図2のように水の深さは3.5cmになりました。またこのおもりを側面が底面につくように入れたところ、図3のように水の深さは4cmになりました。

①この容器の底面積を求めなさい。
②図4のようにこのおもりを円の面が容器の底面につくように2本入れると、
水の深さは何cmになりますか。
(11)
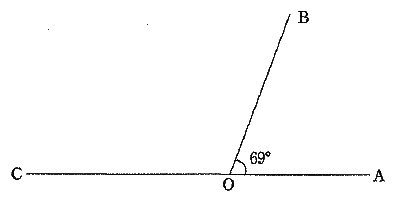
解答らんの図に∠COP=27°の直線OPを作図しなさい。
また、どのように作図したのかも説明しなさい。ただし、コンパスは4回まで使ってよい。
*注意*
定規は直線を引くために用い、目盛りを使用しないこと。
@解説@
(2)

分母が2のべき乗。
1024で通分してもできるが、例題をよくみて見よう。
1/2+1/4=1-1/4=3/4
1/2+1/4+1/8=1-1/8=7/8
1/2+1/4+1/8+1/16=1-1/16=15/16
ということは、
与式=1+(1-1/1024)=2047/1024
(3)①

一番左列の2マスが1~3。2列目の上段に繰り上がると4。
4の倍数が大きな区切りになると予想する。
8は2列目の下、12は2列目の上下→16は3列目上段に繰り上げ。
3→4、12→16の様子が似ている。4のベキ乗で繰り上がる→4進法
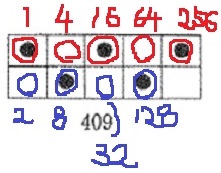
上段は40=1、41=4、42=16、43=64、44=256
下段は2から始まり4倍。(もしくは次の上段の半分)
12のように上段と下段の両方に●があると、その上段の3倍の数。
例題の409は、1+8+16+128+256=409となる。
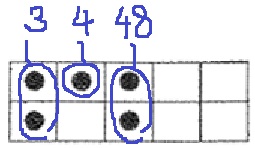
1×3+4+16×3=55
②
275を4進法に直すと、10103。
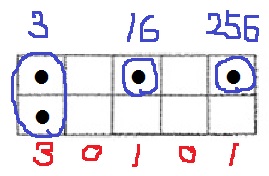
上段・下段どちらもないと0。
上段のみが1、下段のみが2、両方あると3。
0~3の4つの数字で表すのが4進法。
(4)①
推論問題。偶数・奇数の判定がポイント。
1~7は偶数が3つ、奇数が4つ。
『一番左は他6つの平均である』
【平均(一番左)×6=残り6つの総和】
6(偶数)をかけたので、残り6つの総和は偶数になる。
もし、一番左の数字が奇数だと、残りは偶数3つ、奇数3となり、
これらの6つの数字の和は奇数になってしまう。
よって、一番左の数字は偶数。候補は2・4・6。
1~7のうち6つを選んだ平均が2だと小さすぎる。逆に6は大きすぎ。
一番左は4に決まる。
真ん中の数字は4より大きい→5・6・7
1~7の総和は28。
28は偶数なので、奇数を1つ選んで取り除くと残りの6つの数字の和が奇数になる。
しかし、真ん中をはさんで左右の3つの数字の和が等しくなったということは、
6つの数字の和は偶数でなくてはならない。
よって、真ん中の数字は6となる。
②
真ん中が6だから、左右の3つの和はそれぞれ(28-6)÷2=11

左の2つの和は11-4=7。残りの数字では(2、5)の組合せしかない。
『左から2番目と右から2番目の和と、両端の和が等しい』
よって、【4・2・5・6・7・3・1】と決まる。
(5)①
〔1、2、3〕→123+132+231+213+321+312
1、2、3の並べ方は、3×2×1=6通り
筆算をイメージしよう。
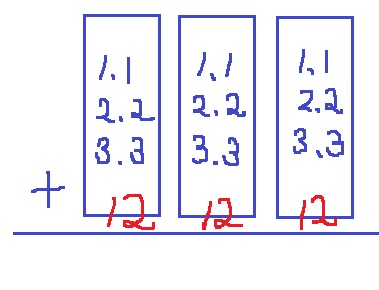
一の位、十の位、百の位のなかで(1・2・3)が2つずつ計6つの数字がでてくる。
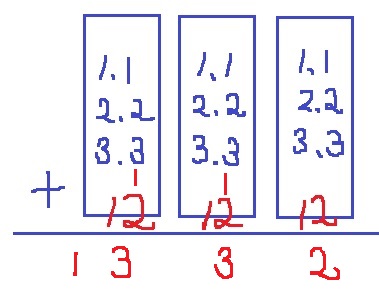
各位のなかで計算。繰り上がりに気を付けよう。
法則さえわかれば、4桁も同様。

4つの数字の並べ方は、4×3×2×1=24通り
各位では(2、4、6、8)が24÷4=6個ずつ。
(2+4+6+8)×6=120
一の位では12を繰り上げ、十の位では13を繰り上げ…と計算して、133320。
②
ここでは分配法則を使ってみる。
〔2、4、6、8〕=120×1+120×10+120×100+120×1000
〔1、3、5、7〕=96×1+96×10+96×100+96×1000
〔2、4、6、8〕÷〔1、3、5、7〕
={(1+10+100+1000)×120}÷{(1+10+100+1000)×96}
=120÷96=5/4
(9)
等しい角に印をつける。
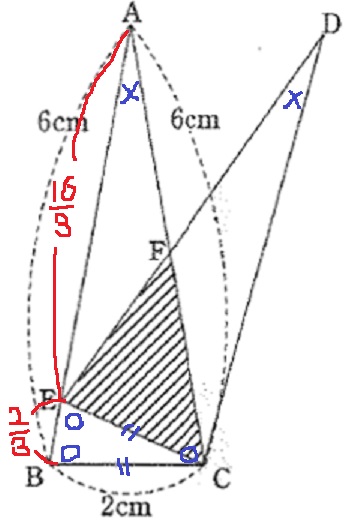
2角が等しい→△ABCと△CBEが相似
AB:CB=CB:EB
EB=2×2/6=2/3
AE=6-2/3=16/3

△ABCの内角は×-○-○
×+○+○=180°
合同から、∠DEC=○
∠FEA=180-∠DEC(○)-∠CEB(○)=×
△AEFは二等辺となる。
さらに、合同から∠EAF(×)=∠CDF(×)
対頂角と合わせて2角が等しく、△AEFと△DCFが相似。
△DCFも二等辺となる。
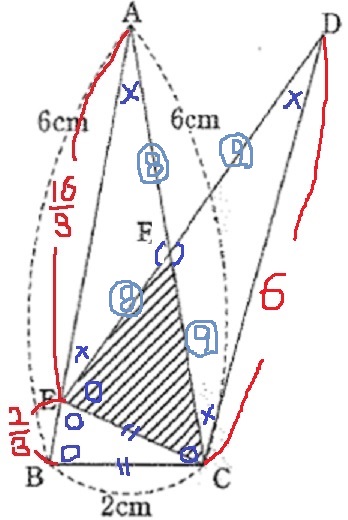
AE:DC=16/3:6=8:9
AF=EF=⑧、DF=CF=⑨
求める解は△CEFは△ABCの面積の何倍かだが、
△DECは△ABCと合同なので、△DECで考えよう。
△DEC:△CEF=DE:FE=17:8
よって、△CEFは△ABCの8/17倍。
(10)①

水面下の体積に注目する。
図2は、水+円柱の高さ3.5cm分。
図3は、水+円柱の高さ7cm分(全部)。
ということは、水面差0.5cmの体積は、
(水+円柱7cm)-(水+円柱3.5cm)=円柱3.5cmに相当する。
容器の底面積は、2×2×3.14×3.5÷0.5=87.92cm2
②
水の体積が変わらないことを利用する。
【体積=底面積×高さ】
底面積と高さは反比例で、各々の比は逆比になる。
前問で、容器の底面積は87.92cm2=28×3.14
円柱1本の底面積は、2×2×3.14=4×3.14
円柱2本の底面積は、8×3.14
容器の底面積を【28】とおく。
円柱1本のときの底面積は、【28】-【4】=【24】
円柱2本のときの底面積は、【28】-【8】=【20】
底面積の比は、円柱1本:円柱2本=24:20=6:5
高さの比は、円柱1本:円柱2本=5:6
よって、3.5×6/5=4.2cm
(12)
27°の作図。コンパスの使用が4回までに制限されている。
69°からどうやって27°をつくればよいか。
180-69×3=27
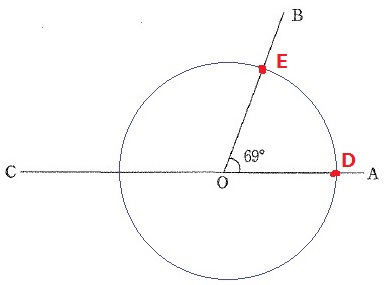
①Оを中心にグルっと円を描く。
ОAとОBの交点をD・Eとする。
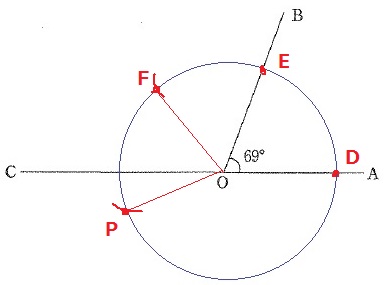
②コンパスでD-Eの距離をとり、Eを起点にFを作成。
③Fを起点にPを作成。
∠EOF=∠FOP=69°
∠POD=69×3=207°
∠POC=207-180=27°となる。
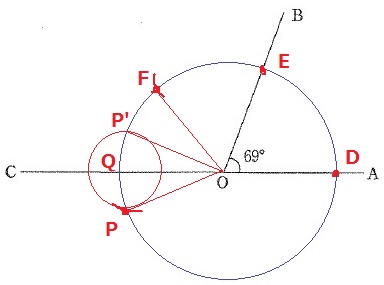
④Qを中心にQPを半径として円を描く。
ACを対称の軸として、Pを上へ対称移動。
∠P’OC=27°でもOK。
■データ■
200点満点中
受験者平均…89.7点 合格者平均…127.6点




コメント