問題PDF
図1のような六角形のライトが、たくさんあります。これを図2のように28個ならべ、
00:00から23:59までの時刻を表すデジタル時計をつくりました。
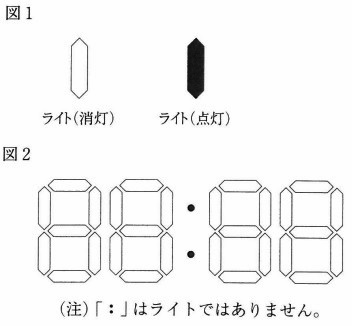
このとき、次の各問いに答えなさい。ただし、0から9までの数字は、
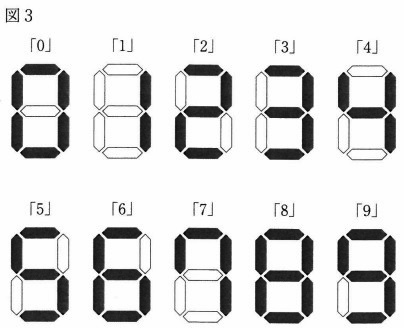
図3のように表すこととし、時または分を表す数が0から9までのときは、
十の位に0を表示します。
例えば、午前2時1分は02:01、午後8時5分は20:02と表します。
(1)と(3)で時刻を答える場合も、02:01、20:05のように表します。
(1)
点灯しているライトの本数がもっとも多い時刻は、何時何分ですか。
(2)
ある時刻にライトが12本点灯していました。
考えられる時刻は何通りありますか。
(3)
ある時刻に点灯しているライトの本数と、その1分後に点灯しているライトの本数を比べます。
点灯しているライトの本数が1分後にもっとも多く増えるのは、何時何分ですか。
考えられる時刻をすべて答えなさい。
@解説@
(1)

それぞれのライトの本数を書いておく。
最も多いのは8、次点は0・6・9。
時間の十の位は0~1、分の十の位は0~5の範囲→08:08
(2)
数字は4ケタなので、1ケタあたりの本数は平均で12÷4=3本
ということは、1は必ずいる。1の本数で場合分け。
◆1が4つ
2×4=8本で×
◆1が3つ
残りは、12-2×3=6本
6本は〔0・6・9〕
【1110】→0がどこにあるかで4通り
【1116】→6は時間と分の一の位だけで2通り
【1119】→同様に2通り
◆1が2つ
残りは、12-2×2=8本
8本は〔4・7〕
時間は11時、14時、17時しかないので書いて調べました。
2桁は必ず1、残りの2桁は4か7で埋める。
【1144】【1147】【1414】【1417】【1441】【1714】【1717】【1741】で8通り
◆1が1つ
残りは、12-2=10本
1以外は最低でも4本なので無い。
合計16通り
(3)

↑再掲
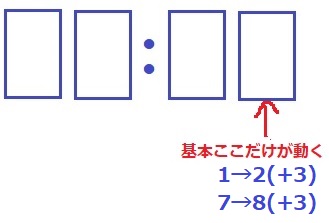
もし繰り上がりがないとすると、分の一の位だけが動く。
この条件で点灯するライトが最も増えるのは、1→2、7→8の+3本
・・さすがにこれが答えではなさそう。
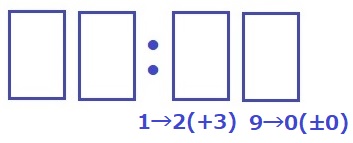
分の一の位が繰り上がるとどうか。
9→0はともに6本で±0本
分の十の位は0~5の範囲で、このうち最も大きいのは1→2の+3本
先ほどと変化なし。ということは、59分から00分の繰り上がりではないか?
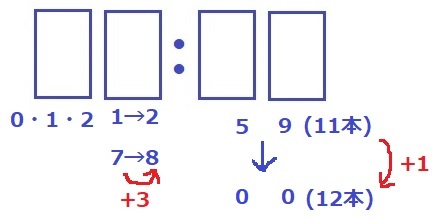
59分→00分で+1本
時間の一の位で1→2、7→8で+3本と合わせれば+4本になる。
時間の十の位は0・1・2だけなので、01:59、07:59、11:59、17:59、21:59
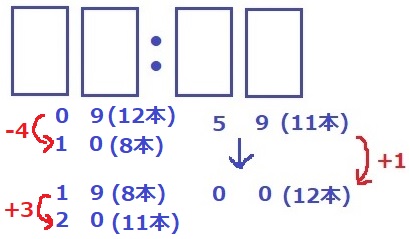
忘れてならないのは、時間の一の位が繰り上がった場合を想定すること!
09時→10時の繰り上げは-4本だが、19時と20時の繰り上げは+3本
分と合わせたら+4本で増加する本数が等しくなる。
したがって、01:59、07:59、11:59、17:59、19:59、21:59



コメント