2024年度　聖光学院中学過去問【算数】大問２解説

問題ＰＤＦ
以下のように、長方形から新たな長方形を作る操作を定めます。

〔操作〕
長方形ＡＢＣＤの縦の辺ＡＢと辺ＣＤの真ん中の点をそれぞれＥ、Ｆとします。
下の図のように、Ｅ、Ｆを通る直線で長方形ＡＢＣＤを切って２つに分けて、
辺ＡＥを辺ＦＣに重ねて新たな長方形ＥＢＦＤを作ります。

たとえば、縦４ｃｍ、横５ｃｍの長方形にこの操作をおこなうと、縦２ｃｍ、横10ｃｍの長方形になります。

縦〔　ア　〕ｃｍ、横〔　イ　〕ｃｍの長方形Ｒにこの操作を続けて何回かおこなうことを考えます。
〔　ア　〕、〔　イ　〕は整数であるものとして、次の問いに答えなさい。

（１）
長方形Ｒにこの操作を７回続けておこなったところ、正方形ができました。
〔　ア　〕：〔　イ　〕を最も簡単な整数比で答えなさい。

（２）
長方形Ｒにこの操作をおこなうごとにできた長方形の周の長さを計算したところ、
８回目の操作後に初めて周の長さが奇数になりました。
〔　ア　〕として考えられる整数のうち、３けたのものは何個ありますか。

（３）
長方形Ｒにこの操作をおこなうごとにできた長方形の周の長さを計算し、
操作前と操作後の周の長さを比べて増加しているか減少しているかを調べたところ、
４回目までの操作の前後ではすべて減少し、５回目の操作の前後では増加しました。
〔　ア　〕÷〔　イ　〕の商として考えられる整数は何個ありますか。

（１）
操作後に長方形の縦が半分、横が２倍になる。
操作を１回戻すたびに、縦が２倍、横が半分になる。

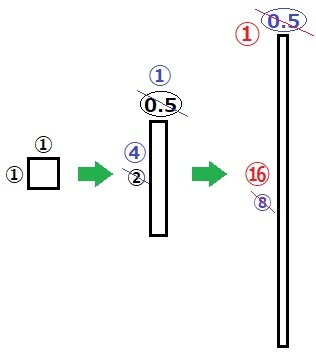
操作７回後の正方形の１辺を①とする。
１回戻すと、縦：横＝②：〇0.5＝４：１
さらに１回戻すと、縦：横＝⑧：〇0.5＝16：１

横の比を１で統一すると、操作１回戻るごとに縦の比は４倍ずつ長くなる。
７回前の縦の比は、４×４×４×４×４×４×４＝16384
縦：横＝16384：１
ア…16384、イ…１

（２）
１回の操作で縦半分、横２倍。
１～７回目まで周の長さは偶数だった。
横は２倍されるので必ず偶数。
また、周の長さ＝（縦＋横）×２だから、８回目後の縦が奇数でも周の長さは偶数になる。
条件を満たす長方形は７回目後の縦が奇数（８回目後に小数点がつく）。
換言すれば、２の素因数を７個だけ含む数である。
２×２×２×２×２×２×２＝128

128に奇数を小さい順にかけていく。
128×１＝128、128×３＝384、128×５＝640、128×７＝896
128×９は４桁だから終わり。
４個

（３）

周の長さが１～４回目までは減少、５回目に増加した。
基本的に長方形が縦長だと操作後に周が短くなり、横長だと長くなる。

縦長から横長に切り替わるタイミングを直接探るのは難しいので、
操作をしても周の長さが変わらない長方形を探し、その前後の長さに見当をつける。

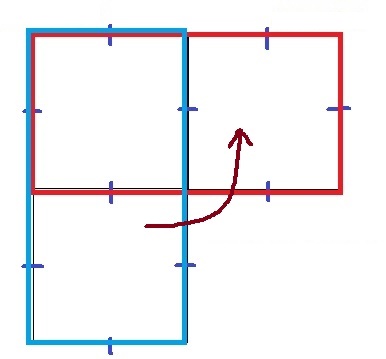
辺の中点で切るので、正方形に区切ると見つけやすい。
左下の正方形を右上に移動させると、長方形の周の長さは変わらない。
縦：横＝２：１→縦：横＝１：２
操作前の横を１とすると、周の長さは縦が２より大きいと減少、２より小さいと増加する。

縦の最小値を探すには、４回目前後が減少ではなく等しい場合を考える。
（５回目後は１：２の横長からさらに横長で増加する。４回目で条件を崩す）

求めたいのはア÷イの商の個数。
横の長さ（イ）を１とおけば、縦の長さ（ア）を調べるだけで条件に合う商の範囲が絞れる。
また、横を１に統一すると、縦の長さの比は（１）より４倍すればいい。
操作をさかのぼると、２×４×４×４＝128
最初の長方形が縦：横＝128：１だと、４回目の前後で周が等しくなって条件不適合。

もし最初の縦が129であれば、３回目後の縦は129÷４÷４÷４で２よりちょっと大きくなる。
縦：横＝２：１の長方形より縦長なので、４回目後は横長でも周の長さは減少するはずである。
５回目後は横長→横長で周の長さが増加する。

縦の上限はどうか？
今度は５回目前後で周の長さが変わらないケースを考える。
最初の長方形の縦は、128×４＝512
もし、最初が511だと、４回目後の縦は511÷４÷４÷４÷４で２を下回る。
→４回目後は減少、５回目後は縦：横＝１：２より横長で増加。

該当する式は、129÷１～511÷１の商。
⇒129～511の個数。
511－129＋１＝383個

＠余談＠

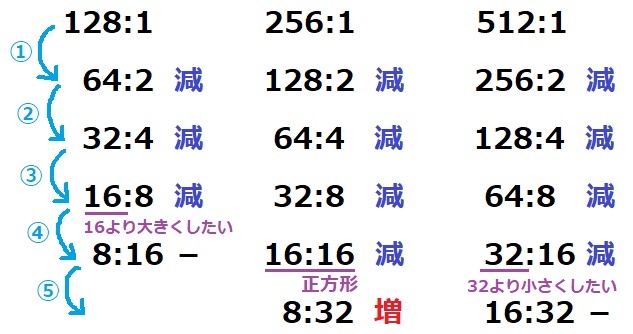
↑全部（縦：横）です。
辺を半分か２倍するので、２のベキ乗にターゲットを絞っても解ける気がする。
（１）より、正方形からさかのぼった操作前の長方形は周の長さが増えた。
正方形は縦と横の長さが等しいから、正方形の操作後も周の長さは増える。
つまり、正方形が作れたら、周の長さが最小となるのは正方形である。

４回目後に正方形になれば、１～４回目は減少、５回目から増加する。
（１）のように横を１で統一すると、最初の縦は４×４×４×４＝256
縦：横＝256：１の長方形は正方形を経由する綺麗な形で増加に転ずる。

１個手前の128：１を調べると、４回目の前後は16：８→８：16（和が24）で変わらない。
縦の長さだけを操作する。（横は１→２→４→８…で増加）
３回目後の縦が16より大きければ、横＋８に対して縦は－８を超えるから４回目後も減少する。
最初の縦は128＋１＝129
１個後ろの512：１では５回目前後が増加しないので、
４回目後の32を小さくすれば増加する。512－１＝511
縦は129～511→383個
（＊２のベキ乗を並べて一方の列を÷２、他方の列を×２すると、256のように同数が登場するか、
128や512のように入れ違いが発生し、入れ違いだと前後の和が等しくなる）
難関中（算数科）解説ページに戻る