問題ＰＤＦ
１を１個、２を２個、３を３個…と並べた数字の列を考えます。
１、２、２、３、３、３、４、４、４、４、５、…
この数字の列を、図のようにマス目に並べます。
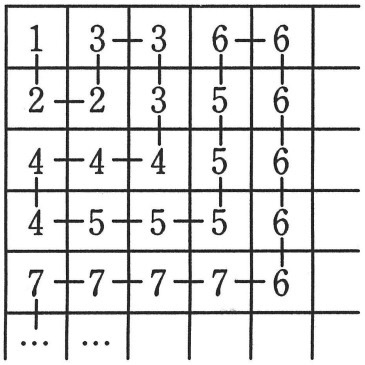
例えば、もとの数字の列の１個目の「５」は、上から４行目、左から２列目にあります。
また、上から３行目、左から５列目の数字は、もとの数字の列の列の４個目の「６」です。
（１）
もとの数字の列の36番目の数字は、何個目の何ですか。
また、上から何行目、左から何列目にありますか。
（２）
もとの数字の列の１個目の「21」は、上から何行目、左から何列目にありますか。
（３）
上から21行目、左から３列目の数字は、もとの数字の列の何個目の何ですか。
＠解説＠
（１）
もとの数列の36番目を求める。
１＋２＋３＋４＋５＋６＋７＋８＝36
もとの数列の36番目は８番目の８である。
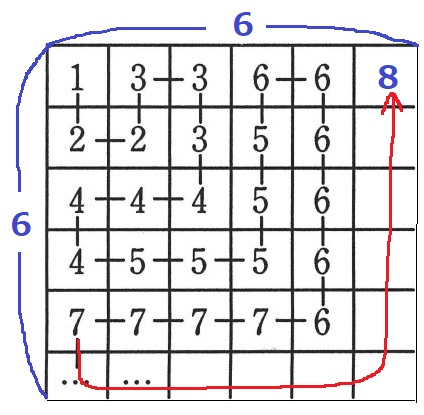
グルグル数列は正方形で捉える。
36は平方数。１辺６個の正方形の右上にくる。（上から１行目、左から６列目）
解答…８個目の８、上から１行目、左から６列目
（２）
もとの数列の１個目の21は何番目かを求める。
（１＋２＋３…＋20）＋１
＝21×20÷２＋１＝211番目
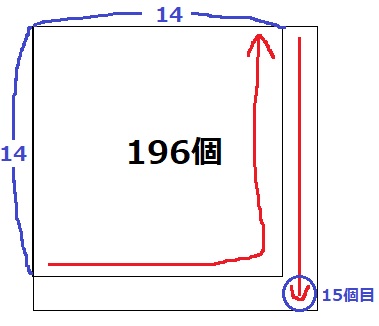
211以下の最大の平方数は14×14＝196
１辺が偶数個の場合、左下から右上に向かうので196番目は１行目14列である。
残りは211－196＝15個→上から15行目、左から15列目
（３）
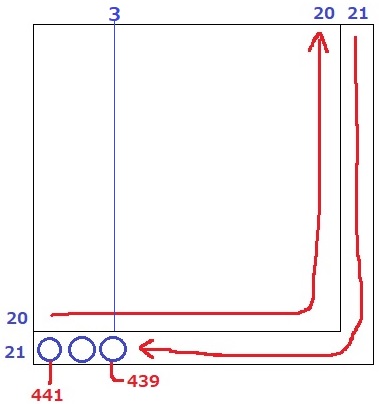
21行目１列目は、21×21＝441番目
21行目３列目は、439番目である。＊441－（３－１）＝439
前問で１個目の21が数列の211番目だったので、30に見当をつけてみる。
１＋２＋３…＋30
＝31×30÷２＝465
行き過ぎたので戻る。465－30＝435
435番目は29の最後（29個目の29）。
439番目は４個目の30となる。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント