問題ＰＤＦ
対角線の長さが８ｃｍの正方形のタイルがあります。このタイルを、回転させることなく、下の図の向きのまま（ア）から（エ）に示すような太線の枠の中を動かします。
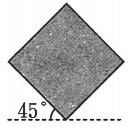
それぞれの場合について、枠の中でタイルが通れない部分の面積を求めなさい。
ただし、枠の厚みや釘の太さは考えないものとします。
＠解説＠
（ア）
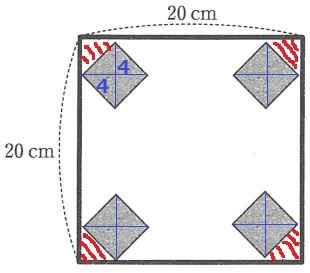
四隅が通れない。
合わせると、１辺４ｃｍの正方形が２つ。
４×４×２＝32ｃｍ2
（イ）
釘が打たれましたワ(´ﾟдﾟ｀)
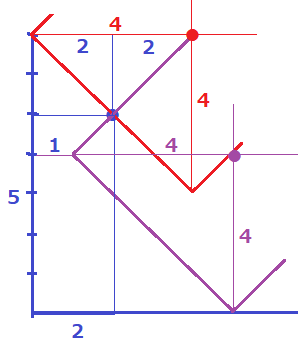
釘の中には入れないので、上と右にタイルをくっつける。
正方形の対角線の半分である４ｃｍと直角二等辺三角形をうまく使い、
左下の通れない部分を確定する(;`ω´)
上にくっつけるとタイルの中点に釘があたる。
右にくっつけると下から５ｃｍのところに釘があるので、
タイルの左の頂点は外枠から１ｃｍ右側で止まる。
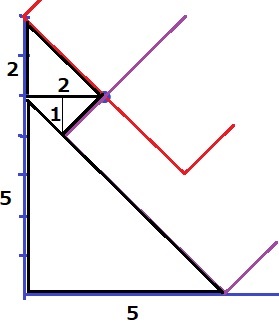
このように分割。
５×５÷２＋２×１÷２＋２×２÷２＝15.5ｃｍ2
残りの３つの角を足し忘れないように！
15.5＋32×３/４＝39.5ｃｍ2
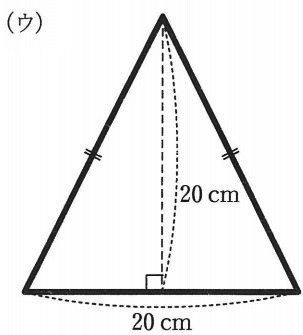
（ウ）
上の部分を調査。
底面積と高さが同じである二等辺三角形と相似。
→対角線が８ｃｍなので、上から８ｃｍのところでタイルが止まる。
通れない部分は、底辺４ｃｍ、高さの合計が８ｃｍである２つの三角形の和。
４×８÷２＝16ｃｍ2
↑図が縦長になってしまいました。。
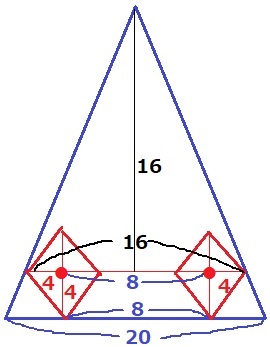
対角線の半分である４ｃｍを手がかりに、タイルの中心は上から16ｃｍ。
左右のタイルの中心は距離が16－４×２＝８ｃｍ。
これを底辺に移動すると、通れない隅の底辺の長さの和は20－８＝12ｃｍ
12×４÷２＝24ｃｍ2
したがって、16＋24＝40ｃｍ2
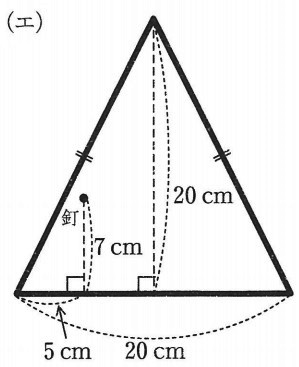
（エ）
難しい:;(∩´＿`∩);:
時間がたっぷりあれば正答率は上がるだろうが、時間内に終わらせるのは至難。
いったん釘を無視する。
前問の図を頼りにタイルが外枠に接したとき、釘がどこにあるかを確定する。
ポイントは、縦と横の比が２：１の直角三角形。
ＡＢ＝４ｃｍ、ＣＢ＝４÷２＝２ｃｍ
Ｂの右３ｃｍ、上７ｃｍに釘がある。
Ａからたどると右に３ｃｍ、上に３ｃｍに釘だから、
ちょうどタイルの辺上に釘があるじゃありませんか⊂( ･∀･) 彡 =͟͟͞͞(✹)`Д´))
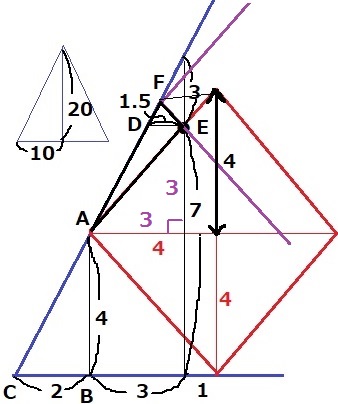
釘の上にもタイルを設置。通れない範囲に△ＡＥＦが追加される。
縦：横＝２：１の直角三角形より、ＤＥ＝３÷２＝1.5ｃｍ
高さの合計はタイルの対角線の半分である４ｃｍに相当する。
△ＡＥＦの面積…1.5×４÷２＝３ｃｍ2
したがって、40＋３＝43ｃｍ2
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント