問題ＰＤＦ
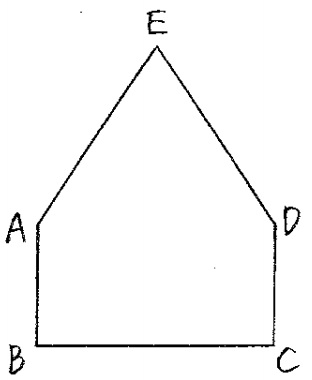
図の五角形ＡＢＣＤＥにおいて、四角形ＡＢＣＤは長方形、三角形ＡＤＥは四角形ＡＢＣＤと面積が等しい正三角形です。次の問に答えなさい。
（１）
直線ＥＢでこの五角形はどのような面積比に分けられますか。
（２）
辺ＤＥのまん中の点をＭとすると、直線ＭＢでこの五角形はどのような面積比に分けられますか。
（３）
次のア、イ、ウを正しくうめなさい。
「（２）の点Ｍと五角形の辺（ ア ）を（イ）：（ウ）に分ける点を通る直線は、
この五角形の面積を二等分します。」
＠解説＠
（１）
△ＡＢＥを変形させる。
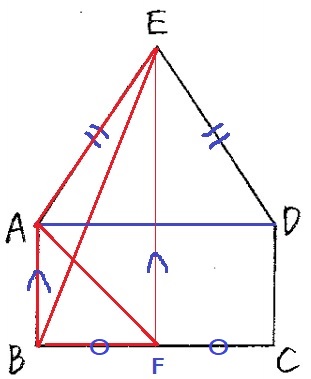
正三角形の頂点Ｅから垂線をおろし、ＢＣとの交点をＦとする。
→ＦはＢＣの中点にあたる。
また、∠ＡＢＦ＝∠ＥＦＣ＝90°で同位角が等しく、ＡＢとＥＦは平行。
等積変形で△ＡＢＥと△ＡＢＦの面積は等しい。
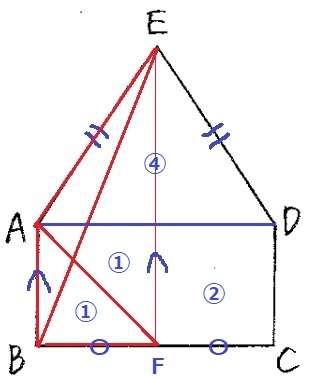
△ＡＢＦの面積を①とすると、長方形ＡＢＣＤの面積は④。
五角形ＡＢＣＤＥ（全体）は④×２＝⑧
△ＡＢＥが①なので、面積比は１：７に分けられる。
（２）
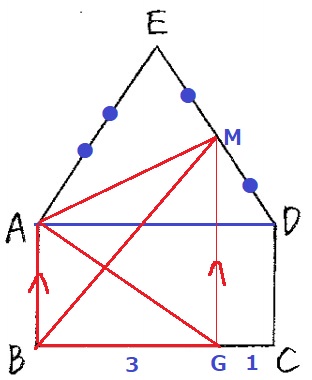
ＭからＢＣに垂線、足をＧとする。
ＢＧ：ＧＣ＝３：１
△ＡＢＭを△ＡＢＧに等積変形。
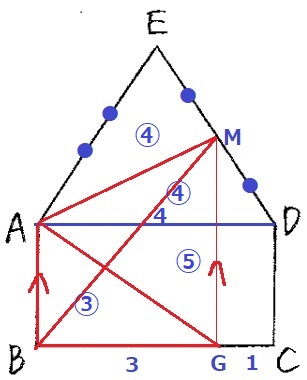
△ＡＢＭ＝△ＡＢＧの面積を③とする。
上底＋下底の和から、四角形ＡＧＣＤは⑤
長方形ＡＢＣＤ＝正三角形ＡＤＥ＝⑧
ＭはＥＤの中点だから、△ＡＭＥは⑧÷２＝④
四角形ＡＢＭＥ＝④＋③＝⑦
全体が⑯なので、残りの四角形ＭＢＣＤは⑨
７：９
（３）
前問の正答が前提条件。
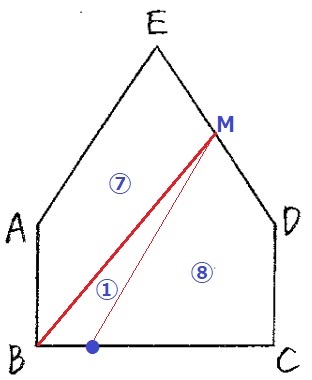
⑦：⑨から⑧：⑧にすれば二等分になる。
ということは、二等分する直線はＢＣを通過する。
面積比から底辺の長さの比を知りたいので、四角形ＭＢＣＤをＭＣで分割。
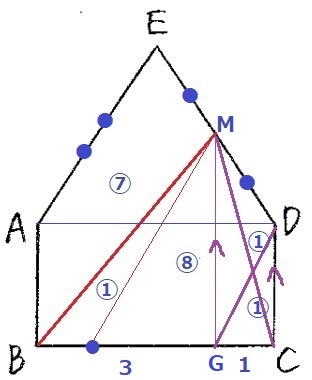
△ＭＣＤを△ＧＣＤに等積変形。
前問と同じ比を使っているので同様の考えで△ＧＣＤ＝△ＭＣＤ＝①
↑四角形ＭＢＣＤ（⑨）をこのように分ける。
面積比から底辺の比は１：７。
ア…ＢＣ、イ…１、ウ…７
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント