問題PDF
(1)
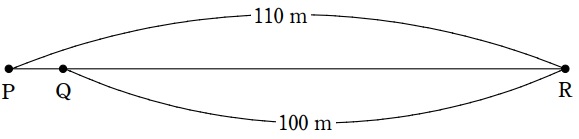
下の図のような直線のコースに3点P、Q、Rがあり、QRの長さは100m、PRの長さは110mです。それぞれ一定の速さで走るAさんとBさんが、このコースを使って2回競走をしました。1回目は、2人ともQから同時にスタートし、Rまで競走をしたところ、AさんがBさんに10mの差をつけて先にゴールしました。2回目は、AさんはPから、BさんはQから同時にスタートし、1回目と同じ速さでRまで競走をしたところ、〔 ア 〕さんが〔 イ 〕mの差をつけて先にゴールしました。このとき、〔 ア 〕にはAかBを、〔 イ 〕にはあてはまる数をそれぞれ答えなさい。
(2)
同じ大きさの白い正三角形のタイルと黒い正三角形のタイルが、それぞれ4枚ずつ合計8枚あります。この8枚の中から4枚を選んでぴったりとくっつけて大きい正三角形を作るとき、大きい正三角形は何通り作ることができますか。ただし、異なる向きから見ると同じものは、1通りと数えることとします。
(3)
ある中学校の全校生徒の男子と女子の人数の比は5:4です。また、通学に電車を利用している生徒と利用していない生徒の人数の比は10:17です。通学に電車を利用している男子の人数が180人で、通学に電車を利用していない女子の人数が240人のとき、全校生徒は何人ですか。
(4)
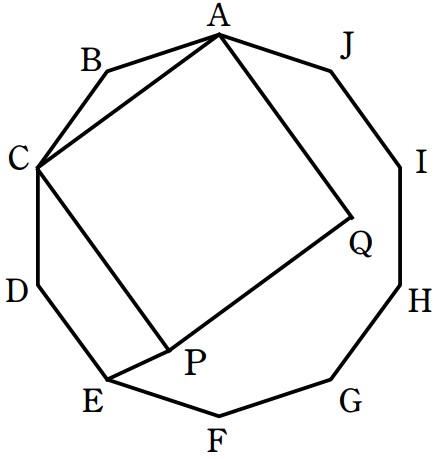
下の図のように正十角形ABCDEFGHIJがあり、ACを1辺とする正方形ACPQを正十角形の内側につくります。このとき、角CPEの大きさは何度ですか。
@解説@
(1)
100m走ではAがゴールするとBは90m地点にいた。
時間一定→速さの比は距離の比なので、A:B=100:90=⑩:⑨
次にAは110mを走る。Aがゴールするとき、Bが走った距離は110×⑨/⑩=99m
よって、Aが先にゴールして、100-99=1mの差がつく。
ア…A、イ…1
(2)
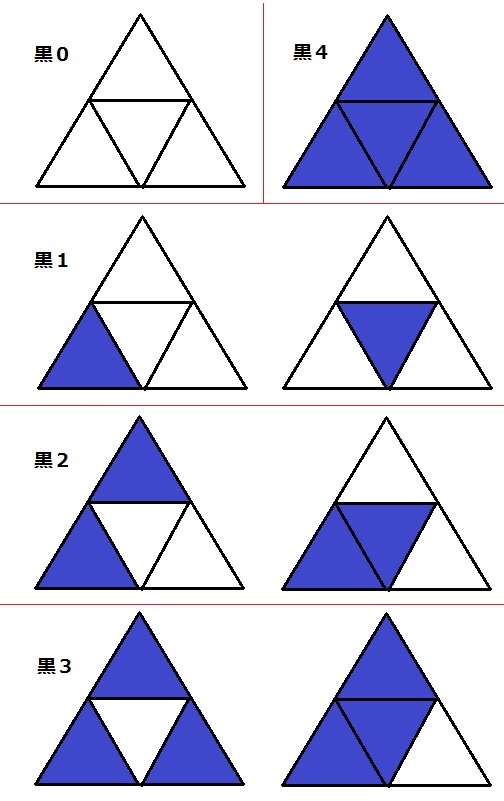
4つの正三角形のうち、中の有り無しには個性がでる。問題は外側の3つ。
3つだけだと頂点1つ飛ばし、2つ飛ばしなどがないから、クルクル回すと1通りしかない。
黒の枚数で場合分けして調べると8通り。
(3)
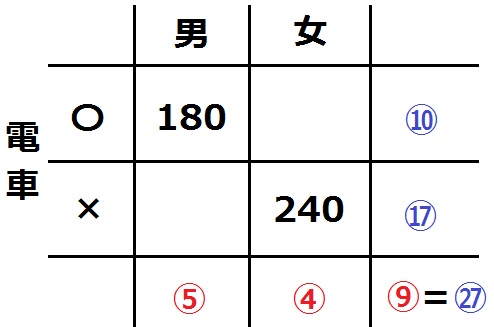
男:女=⑤:④
電車の〇:×=⑩:⑰
全校生徒は⑨=㉗であることに注目する。
赤の比を3倍して青に統一する。
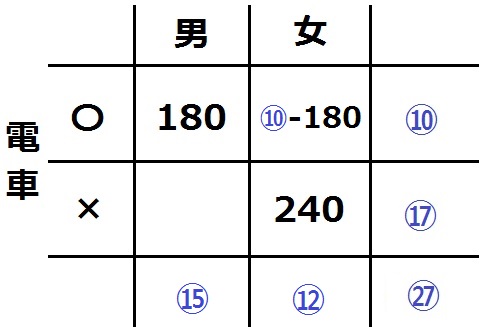
女の〇は、⑩-180人。
女の人数は、(⑩-180)+240=⑫
②=60
①=30人
全校生徒は㉗だから、30×㉗=810人
(4)
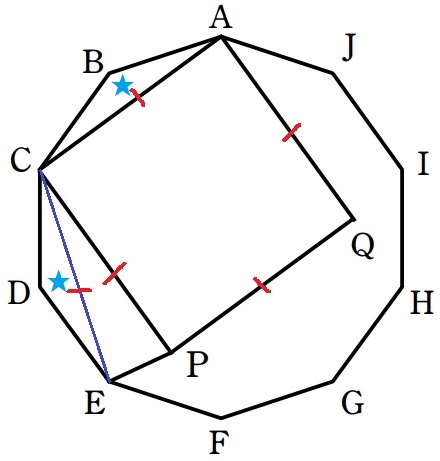
CEに補助線。
△ABCと△CDEは正十角形の隣り合う2辺を等辺とする二等辺三角形で、
あいだの角度が内角で等しいから合同。
AC=CEより、△CEPは二等辺三角形である。
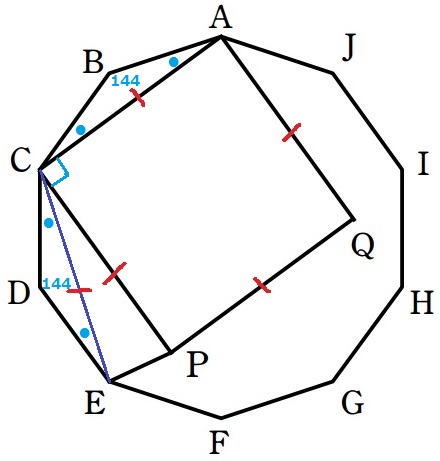
正十角形の1つの内角は、180×(10-2)÷10=144°
●●=180-144=36°
∠ECP=144-(36+90)=18°
∠CPE=(180-18)÷2=81°



コメント