2019年度　明治大学付属明治中学過去問【算数】大問４解説

問題ＰＤＦ
ある回転寿司点では、いくつかの寿司皿がすでにレーンに出ていて、これに５秒に１皿の割合で寿司皿がレーンに追加されます。Ａ、Ｂの２つの団体がこのお店でお寿司を食べるとき、レーンの皿がはじめの２/３まで減るのに、Ａだけだと10分、Ｂだけだと４分かかります。Ａが５皿のお寿司を食べる間にＢは８皿のお寿司を食べるとき、次の問いに答えなさい。ただし、ＡとＢはそれぞれ一定の割合でお寿司を食べるものとします。

（１）
Ａは１分間に何皿のお寿司を食べますか。

（２）
初めにＡだけで８分間食べ、次にＢだけで食べるとき、レーンの皿がなくなるまでには、
Ａが食べ始めてから何分何秒かかりますか。

＠解説＠
（１）

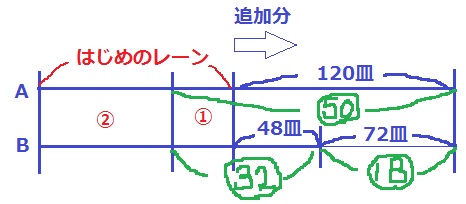
左がはじめのレーン、右が新たに追加される分。
はじめのレーンの２/３まで減るのに、Ａは10分かかった。
１分間に12皿追加されるので、新たに追加された分は12×10＝120皿
Ｂは４分なので、12×４＝48皿追加される。

また、Ａが５皿食べる間にＢは８皿食べる。
１分間で食べる量を、Ａ：Ｂ＝⑤：⑧とおく。
Ａは10分間で、⑤×10分＝㊿食べる。
Ｂは４分間で、⑧×４分＝㉜食べる。
120皿－48皿＝72皿が、㊿－㉜＝⑱に相当する。
①＝72皿÷⑱＝４皿
㊿＝200皿
１分間でＡが食べる皿は、200皿÷10分＝20皿

（２）
はじめのレーンにあった皿の１/３は、200－120＝80皿
はじめのレーンは、80×３＝240皿あった。

１分間でＡは20皿食べ、新たに12皿追加されるので、
１分間に８皿ずつ減る。
最初の８分では、８×８＝64皿減る。
８分後の残りの皿は、240－64＝176皿

１分間で食べる量はＡ：Ｂ＝⑤：⑧なので、
Ｂは１分間に、20×８/５＝32皿食べる。
新たに追加された分を差し引くと、１分間で32－12＝20皿ずつ減っていく。
176÷20＝８・４/５＝８分48秒
よって、８分＋８分48秒＝16分48秒
難関中（算数科）解説ページに戻る