2021年度　豊島岡女子学園中学１回目過去問【算数】大問２解説

問題ＰＤＦ
（１）
４つの整数Ａ、Ｂ、Ｃ、Ｄがあります。ＡとＢとＣの和は210、ＡとＢとＤの和は195、
ＡとＣとＤの和は223、ＢとＣとＤの和は206です。このとき、Ａはいくつですか。

（２）
豊子さんと花子さんは、同時にＡ地点を出発し、
Ａ地点とＢ地点の間をそれぞれ一定の速さで１往復します。
２人はＢ地点から140ｍの場所で出会い、豊子さんがＡ地点に戻ったとき、
花子さんはＢ地点を折り返しており、Ａ地点まで480ｍの場所にいました。
このとき、（豊子さんの速さ）：（花子さんの速さ）を求めなさい。

（３）
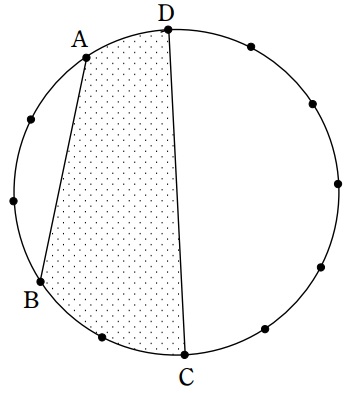
下の図のように、円周を12等分した点をとり、
点Ａと点Ｂ、点Ｃと点Ｄをそれぞれまっすぐ結びました。
直線ＡＢの長さが６ｃｍであるとき、色のついている部分の面積は何ｃｍ²ですか。

（４）
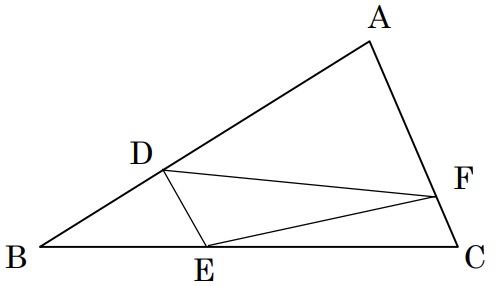
下の図の三角ＡＢＣにおいて、ＡＤ＝９ｃｍ、ＤＢ＝６ｃｍ、ＡＦ＝８ｃｍ、ＦＣ＝２ｃｍで、
（三角形ＢＤＥの面積）：（三角形ＤＥＦの面積）＝２：３です。
このとき、（三角形ＣＥＦの面積）：（三角形ＡＢＣの面積）を求めなさい。

（２）

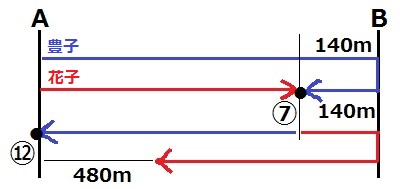
豊子がＢを折り返して140ｍのところで花子と出会った。
このとき、豊子と花子の差は、140×２＝280ｍ
一方、豊子がＡに着いたとき、花子との差は480ｍ。

速さが一定の場合、時間が経つほど差も一定に広がるから、距離の差の比＝時間の比。
280：480＝⑦：⑫
２人が出会った時間が⑦、豊子がＡに着いた時間が⑫。

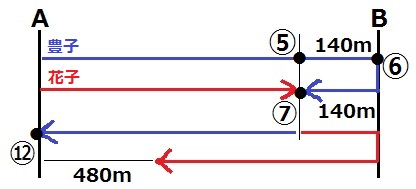
豊子の片道にかかる時間は、⑫÷２＝⑥
⑥で折り返し、140ｍ移動したら⑦の時間になった。
ということは、豊子がＢに着いた⑥より140ｍ手前にいる時間は⑤。
同じ距離にかかる時間の比は豊子：花子＝⑤：⑦
速さの比は逆比で７：５。

（３）

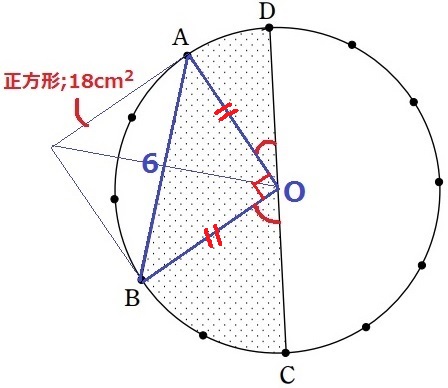
円の中心ＯからＡＯとＢＯをひく。
弧ＡＢは円が12等分されたうちの３つ分なので、∠ＡＯＢ＝360×３/12＝90°
半径よりＡＯ＝ＢＯだから、△ＡＢＯは直角二等辺三角形。
これと同じ直角二等辺三角形をくっつけると正方形になる。
正方形の面積は、６×６÷２＝18ｃｍ²
これはＡＯ×ＢＯ、つまり、半径×半径の値が18である。

求積すべき図形は、直角二等辺三角形（正方形の半分）と弧３つ分の扇形だから、
18÷２＋18×3.14×３/12
＝23.13ｃｍ²

（４）

奇妙な面積比を使う。
ＢＤ：ＤＡ＝６：９＝②：③
△ＢＤＥ：△ＤＥＦ＝②：③
・・これは偶然だろうか？

ＡＥに補助線。
△ＢＤＥ：△ＤＥＡ＝ＢＤ：ＤＡ＝②：③
△ＤＥＡ＝△ＤＥＦ＝③
底辺ＤＥが共通で面積が等しい⇒等積変形でＤＥとＡＦが平行。

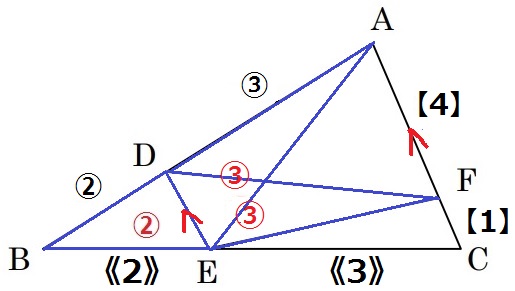
平行線から、ＢＥ：ＥＣ＝ＢＤ：ＤＡ＝２：３
隣辺比で面積比を算出する。
△ＣＥＦ…《３》×【１】＝３
△ＡＢＣ…《５》×【５】＝25
△ＣＥＦ：△ＡＢＣ＝３：25
難関中（算数科）解説ページに戻る