2018年度　フェリス女学院中学過去問【算数】大問５解説

問題ＰＤＦ
ある町の人口を2000年から2015年まで５年ごとに調べたら、
表のようになりました。次の問いに答えなさい。

（１）
2015年の人口は、2010年の人口の何倍ですか。

（２）
2010年の人口は、2005年の人口の1.25倍に増えていました。
2005年の人口は何人ですか。

（３）
仮に、2000年から2015年まで５年ごとに、同じ倍率で人口が変化したと考えたとき、
次の問いに答えなさい。
①この倍率は何倍ですか。
②①で求めた倍率を用いて、この町の2020年の人口を予測すると、何人ですか。

＠解説＠
（１）

17280÷12000＝144/100＝1.44倍
*人口は増えるので、値は１倍を超える。

（２）
12000×１/1.25＝9600人

（３）①
『2000年から2015年まで５年ごとに、同じ倍率で人口が変化した』とする。
→2000年と2015年の変化率を５年ごとに均す。
2000年：10000人　2015年：17280人
17280÷10000＝1.728

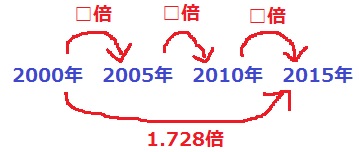
□には同じ値がはいる。
□×□×□＝1.728
立方根は小学生は知らないので、素直に素因数分解します。
1.728＝1728/1000＝（２⁶×３³）/10³＝（４^３×３³）/10³＝12³/10³
よって、□は12/10＝1.2倍

②
17280×1.2＝20736人
前問さえできればサービス問題。
難関中（算数科）解説ページに戻る