2021年度　女子学院中学過去問【算数】大問５解説

問題ＰＤＦ
図のような立方体の展開図の面に１から６までの整数を１つずつ書きます。

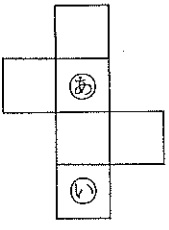
組み立てたとき、３組の向かい合う面の数の和がすべて異なり、
いずれも７にならないようにします。
面（あ）に「６」を書いたとき、面（い）に書くことができる数をすべてあげなさい。

＠解説＠
意外と時間かかります:( ´ω` ):

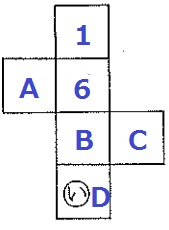
記号をふって整理する。
Ｄ（い）に１は入らないので適当に配置。
Ａ＋Ｃ ≠ １＋Ｂ≠ ６＋Ｄ ≠ ７
残りの２～５を考える。
◆Ｄ＝５
６＋５＝11
他の２数で和が11は作れない。
Ａ＋Ｃ＝２＋４、１＋Ｂ＝１＋３　ＯＫ！

◆Ｄ＝４
６＋４＝10
これも他の２数で和が10は作れない。
Ａ＋Ｃ＝２＋３、１＋Ｂ＝１＋５
Ａ＋Ｃ＝３＋５、１＋Ｂ＝１＋２　ＯＫ！

◆Ｄ＝３
６＋３＝９
Ａ＋Ｃ＝２＋５＝７は×。
Ａ＋Ｃ＝４＋５＝９は和が重なる。×
Ａ＋Ｃ＝２＋４＝６も１＋Ｂ＝１＋５と和が重なり×！
Ｄ＝３はない。

◆Ｄ＝２
６＋２＝８
Ａ＋Ｃ＝４＋５＝９、１＋Ｂ＝１＋３＝４　ＯＫ！
したがって、２・４・５