2021年度　女子学院中学過去問【算数】大問６解説

問題ＰＤＦ
右端から左端までが20ｍのプールを兄と妹が往復します。
兄は一定の速さで泳ぎ、１往復するごとに10秒間休みますが、妹は一定の速さで泳ぎ続けます。
２人は同時に泳ぎ始め、妹が16ｍ泳いだときに初めて兄とすれちがい、
兄がちょうど５往復したときに妹はちょうど４往復しました。
（１）
「泳ぎ始めてからの時間（秒）」と「プールの右端との距離（ｍ）」の関係を、
兄はで 妹はで途中までグラフに表します。
グラフ①からグラフ④のうち、正しいグラフは〔  　　〕で、アにあてはまる数は〔  　　〕です。

（２）
妹は20ｍ泳ぐのに〔　　〕秒かかります。

（３）
２人が２回目にすれちがうのは、泳ぎ始めてから〔　　〕秒後です。

（４）
２人が（３）ですれちがった地点と同じ地点で次にすれちがうのは、
泳ぎ始めてから〔　　〕秒後です。

＠解説＠
（１）

兄の方が速いので、の方が周期が短い→①か②
兄は『１往復するごとに10秒間休む』ので、行って帰ってから横線。
グラフ①
アは片道の20ｍ。

（２）
最初のすれちがいまでに、兄は折り返して24ｍ、妹は16ｍ泳いでいる。
速さの比は、兄：妹＝24：16＝３：２

『兄がちょうど５往復したときに妹はちょうど４往復』
兄は40×５＝200ｍ、妹は40×４＝160ｍ泳ぐ。
速さの比から計算すると、兄は160×３/２＝240ｍ泳ぐはずだが、
40ｍ少ないのは40秒間休憩していたから。（５往復後の休憩は４回に注意！）
兄は40秒で40ｍ泳ぐと考えられるので、兄の速さは秒速１ｍ。
妹は秒速２/３ｍ。
妹は20ｍ泳ぐのに、20÷２/３＝30秒かかる。

（３）

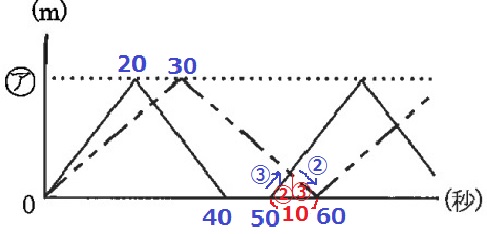
２回目のすれちがいがおこる時間の前後を調べる。
50秒後に兄が再出発、60秒後に妹が戻ってくる。
速さの比が③：②だから、時間の比は②：③
50＋10×②/③＝54秒後

（４）

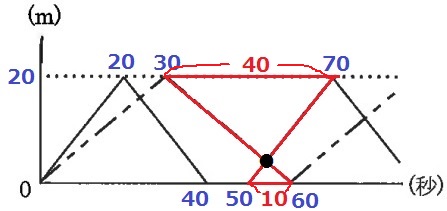
赤いチョウチョウ型の相似に注目。
上が40、下が10のときに辺の比が４：１となり、交差するポイントが（３）と同じである。

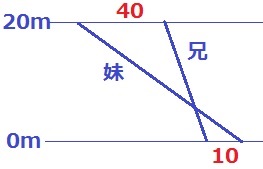
すれちがいではなく、兄が妹を追い越すパターンもあるのでは？
と思われるが、これはない。
（２）より妹は20ｍ泳ぐのに30秒かかるが、うえのグラフでは少なくとも50秒かかっている。

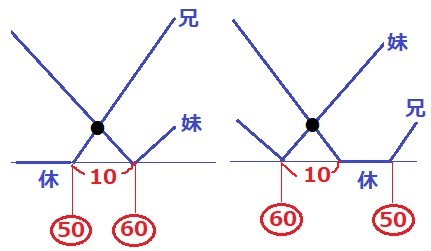
妹がスタート地点を再出発するのは60秒周期。
兄がスタート地点を最出発するのは50秒周期だが、
兄の休憩前に差が10秒になる場合もあるので、〔50の倍数－10〕も検討する。

妹；120・180・240
兄；90・100・140・150・190・200
妹180秒、兄190秒で差が10秒。

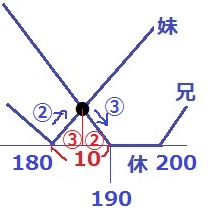
↑50の倍数－10だから兄の休憩前。グラフだとこんな感じ。
180＋10×③/⑤＝186秒後
難関中（算数科）解説ページに戻る