2017年度　早稲田中学過去問【算数】大問３解説

問題ＰＤＦ
１時間に12分ずつ遅れる置き時計があります。
この置き時計を２月１日午前９時に正しい時刻に合わせました。
次の問いに答えなさい。

（１）
正しい時刻で２月１日午前９時から午後４時までの間に、
置き時計の長針と短針は何回直角をつくりますか。ただし、午前９時を１回目とします。

（２）
置き時計が２月１日午後３時４分を示すとき、正しい時刻は午後何時何分ですか。

（３）
正しい時刻で２月１日午前11時から午前11時30分までの間に、
置き時計の10時の方向と短針がつくる角を長針が二等分するとき、
正しい時刻は午前何時何分ですか。

９時00分をはじめの１回の直角とカウントしたとき、
長針が１周するあいだに短針と直角になる回数は２回ある。
また、置き時計の２時から２時36分のあいだに直角は１回できる。
（文字盤の２から90°時計回りに進んだ５から６のどこかに長針があるとき）
よって、２×５＋１＝11回

（２）
午前９時00分～午後３時４分までの時間を求める。
60×６＋４＝364分

針の進む速さは、正しい時刻：置き時計＝⑤：④なので、
正しい時刻では、364×⑤/④＝455分＝７時間35分
午前９時から７時間35分後→午後４時35分

（３）
正しい時刻では１時間に長針は360°、短針は30°回転するので、
長針と短針の速さの比は、長針：短針＝360：30＝12：１
これは１時間に48分しか進まない置き時計でも速さの比は変わらず12：１。

正しい時刻で午前11時～午前11時30分は、午前９時から120～150分後。
これを置き時計に換算すると、
120×④/⑤＝96分、150×④/⑤＝120分
つまり、置き時計では９時から96～120分後（10時36分～11時00分のあいだ）

この間に、『置き時計の10時の方向と短針がつくる角を長針が二等分する』状況を作図する。

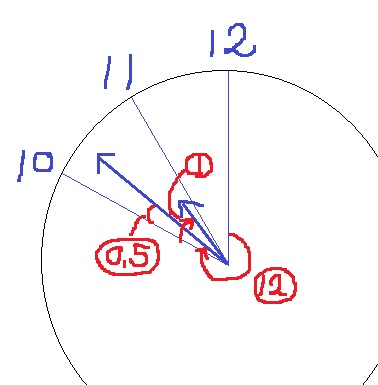
長針は12から⑫、短針は10から①進む。
等角の大きさは〇0.5にあたる。
⑫－〇0.5＝〇11.5が50分なので、長針が進んだ⑫は、
50×12/11.5＝1200/23分（＝52・４/23分）
10時から1200/23分なので、９時から計算すると、1200/23＋60＝2580/23分

以上は置き時計の話で、これを正しい時刻に変換すると、
2580/23×５/４＝3225/23分＝140・５/23分＝２時間20・５/23分
午前９時から２時間20・５/23分後である、午前11時20・５/23分が答え。
難関中（算数科）解説ページに戻る