問題PDF
図1のような円すいがあります。
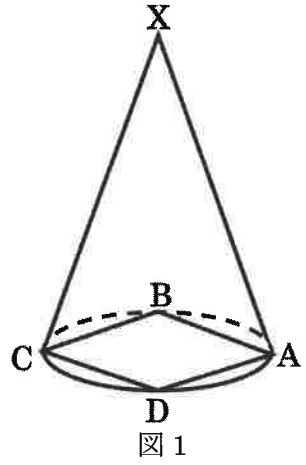
この円すいの側面を直線XAに沿って切りひらくと、円の4分の1であるおうぎ形になります。また、円すいの底面の円には、すべての頂点が円周上にあるような正方形ABCDが書いてあります。正方形ABCDの1辺の長さは10cmです。
(1)
XAの長さは底面の円の半径の長さの何倍ですか。
この円すいの表面上を動く点Pと点Qを考えます。
点Pは図2のように、Aを出発して円すいの側面を最短距離で左回りに1周してAに戻ってきます。一方、点Qは、図3のように、Aを出発して正方形ABCDの辺上を左回りに1周してAに戻ってきます。点Pと点Qは同時にAを出発して、それぞれ一定の速さで動きます。点Pは速さは点Qの速さの4倍です。このとき、円すいを真上から見ると、点Pは図4の実線部分に沿って動いていました。

(2)
点PがAを出発してから、再びAに戻るまでに移動した距離を答えなさい。
また、点PがAに戻ったときの点Qの位置を、次の①~⑧の中から選び、記号で答えなさい。
①A ②AとBの間 ③B ④BとCの間
④C ⑤CとDの間 ⑥D ⑦DとAの間
(3)
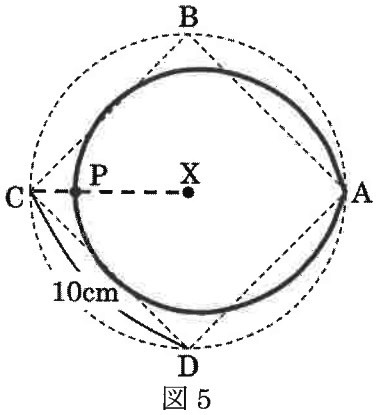
図5は、あるときに円すいを真上からみた図で、3点C、P、Xは一直線上にありました。
このとき、実際のXPの長さ(円すいの頂点から点Pまでの長さ)と、
図5のXPの長さ(真上から見たときのXPの長さ)を答えなさい。
(4)
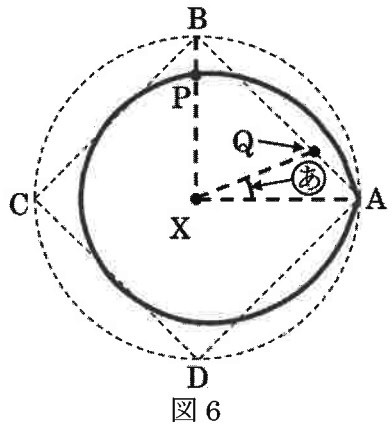
図6は、あるときに円すいを真上から見た図で、3点B、P、Xは一直線上にありました。
(ア)Aを出発してからこのときまでにかかった時間は、
点Pが1周する時間の1/4倍の時間と比べて、長いですか、短いですか、同じですか。
次の①~③の中から選び、記号で答えなさい。
①長い ②短い ③同じ
(イ)図6の(あ)の角度を答えなさい。
(ウ)図6のXPの長さは、図6のXQの長さと比べて、長いですか、短いですか、同じですか。
次の①~③の中から選び、記号で答えなさい。また、その理由も書きなさい。
①長い ②短い ③同じ
(5)
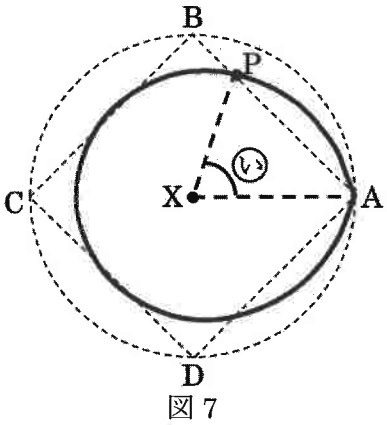
図7は、あるときに円すいを真上から見た図で、点Pは辺AB上にありました。
図7の(い)の角度を答えなさい。
@解説@
(1)
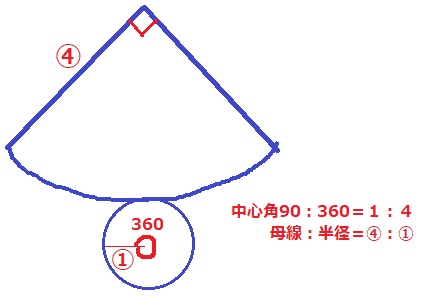
中心角の比と、母線:半径の比は逆比。
XA(母線)は底面の円の半径の4倍。
(2)
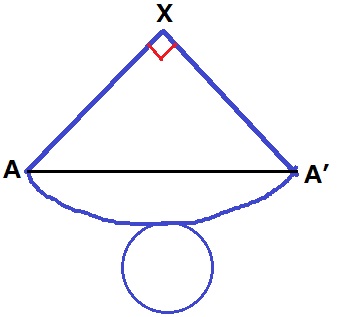
最短距離なので、Pが動いた長さはAA’になる。
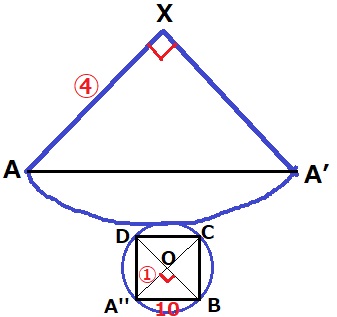
↑Aが3つでてくるので、A’’にしました。
長さは底面に描かれた正方形の1辺10cmしかわかっていない。
対角線AC、BDの交点をOとする。
△XAA’と△OA’’Bがともに直角二等辺三角形で相似。
AA’:AB=④:①
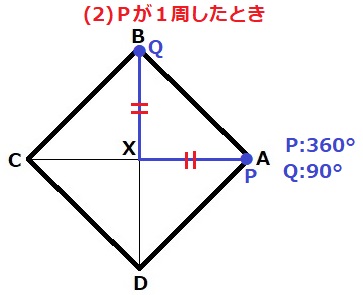
Pが動いたAA’=10×④=40cm
Pが1周して40cm移動。
距離の比は速さの比と同じだから、Qの移動距離は10cm。よって、Bの位置。
点Pが移動した距離…40cm、点Qの位置…③
(3)
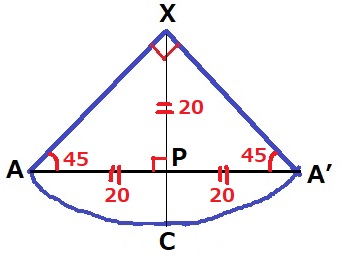
Cは弧AA’の真ん中。
XCとAA’との交点PはAA’の中点である。
直角二等辺XAA’を真っ二つにした、△XAPと△XA’Pも同様に直角二等辺。
XP=40÷2=20cm
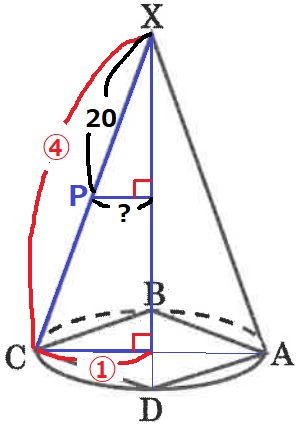
図5は上から見た図だが、正面から見た図だと三角形の相似が使える。
上から見たときのXPは?の長さにあたる。
相似比4:1を利用して、?=20×1/4=5cm
実際のXPの長さ…20cm 図5のXPの長さ…5cm
(4)ア
このあたりから難易度が上がってくる。。
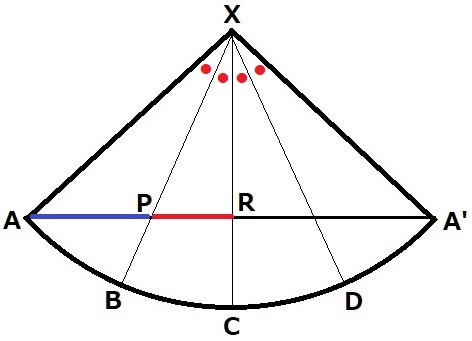
XBとAA’の交点がP。
AA’の中点をRとすると、なんとなくAP>PRに思える。。
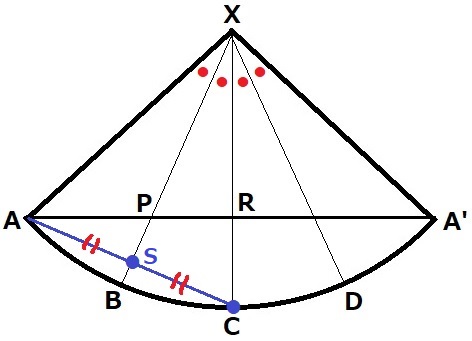
ACをひき、XBとの交点をSとする。
XBを対称の軸として、線対称からAS=CS
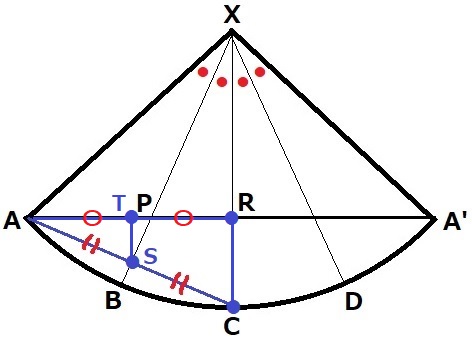
Sを通るRCに平行な線をひき、ARとの交点をTとする。
△ATSと△ARCの相似を利用すると、ARの中点はTである。
PはTの右側にあるので、PがAA’を1周する時間の1/4倍より長いことになる。①
@別解@

もう1つのやり方としては、高校数学に出てくる角の二等分線の証明が使える。
Rを通るAXに平行な直線と、XPの延長との交点をSとする。
錯角で∠XSR=●
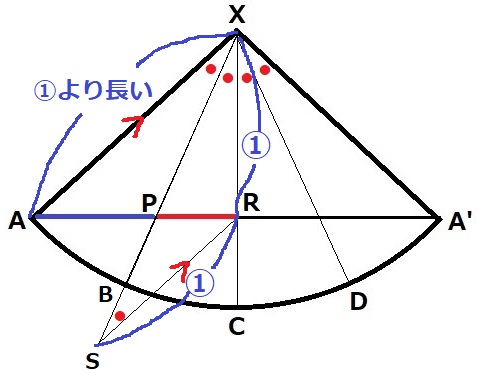
2つの底角が等しいから、△XSRは二等辺三角形。
AR=①とすると、SR=①
直角二等辺三角形XRAの斜辺XAは①よりも長い。
△AXPと△RSPは2角が等しく相似。
対応する辺の比から、XA:SR=AP:RP
XA>SRだから、AP>RPが言える。
イ

(あ)の角度は円錐を上から見た図だが、Qの情報が少ない・・。
そこで、PとQに何かしらの関係があるのではないか?とにらむ。

PとQの位置を図示すると、形が似ている。

(1)より、母線XA:半径XA=④:①
進んだ長さから、AP:AQ=【4】:【1】
これらと45°を合わせると、2辺の比とあいだの角が等しいので△XAPと△XAQが相似!
∠AXPは90°の4分の1だから22.5°である。
対応する角で∠AXQ(あ)=∠AXP=22.5°
ウ
まぐれ当たり防止のためか、解答に説明が要求される(´゚д゚`)

先ほどの相似から、実際のXPとXQの長さは〔4〕:〔1〕
側面の展開図を上からみたとき、長さがどれほど縮まるかを検証する。
展開図のXAの長さ④は上から見た図ではXB①にあたる。
XBの長さは半径よりXAと同じ。
ということは、側面の展開図を1/4倍縮小すると上から見た図の長さになる!
上から見た図のXPは、〔4〕×1/4=〔1〕だから、XPとXQの長さは同じ。
(5)
これはヤバめ:(っ`ω´c):
算数オリンピックはよく知らないけど、そういうのに出てきそうな感じがする。
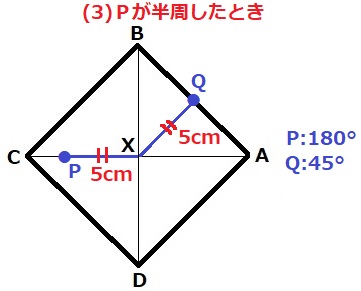

(3)はQがなかったので試しに調べると、半周だからAとBの中点である。XQ=5cm
結果を観察してみると、どれもXP=XQ、∠PXA:∠QXA=4:1。
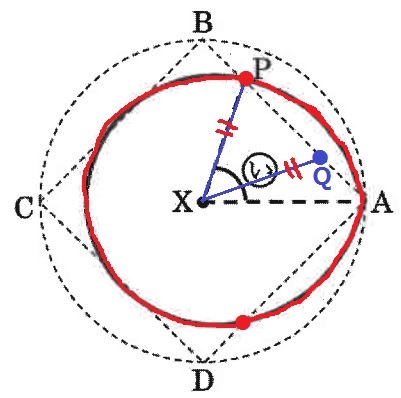
急に消えたQを再現する。
ひょっとするとXP=XQは常に成り立つのでは?
おまけに、∠PXA:∠QXA=4:1も成り立ちそう。
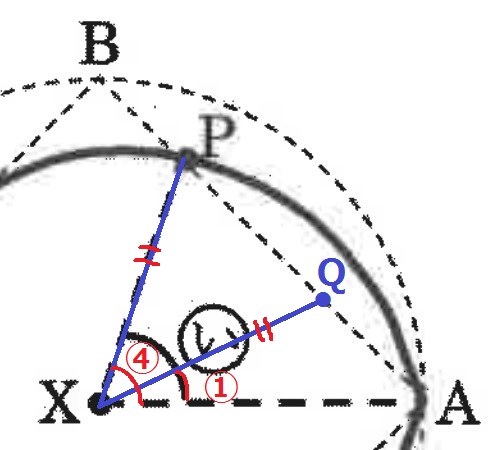
∠PXA=④とすると、∠QXA=①

直角二等辺三角形XABとXP=XQの対称性より、∠PXB=∠QXA=①
(い)=90×④/⑤=72°
@余談@
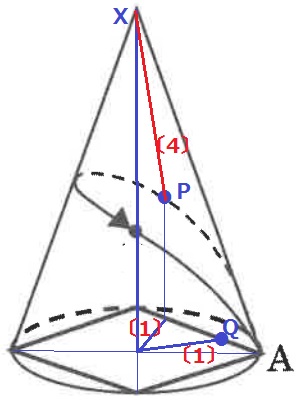
長さについては(4)ウで示したとおり、相似比が4:1の三角形から、
大きい三角形を上から押し込むと1/4倍に圧縮されて等しくなる。
問題は角度がどうして∠PXA:∠QXA=4:1になるのか・・。

(4)アではB・P・Xが一直線上にあるとき、PはAA’の1/4より長い距離を移動していた。
角速度は一定ではないが、相似より対応する角の大きさは常に等しいので、
∠PXAと∠QXAの動きはシンクロしている。
線分の端っこを移動しているときは角の開きは遅いが、Xの真下に近づくと角の開きは速くなる。
Qの速さを4分の1にしてゴールをBまでにしたのは、2つの角の動きを同じにするためだと思う。
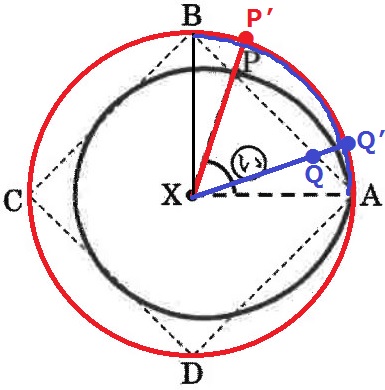
真上からみると、Pの軌道は円ではないくせに∠PXA:∠QXA=4:1となるのは何故か。
PをP’、QをQ’に移動させ、同一円周上を動く2点で捉えてみると、
P’は1周で変な動きをする。Q’は1/4周で変な動きをする。
2つの変な動きは互いにシンクロしているので、ある時間での角の大きさは4:1になるのだと思う…。



コメント