平均59.0点（前年比；＋5.7点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）―68.3％
（１） 85.3％
１－６2÷９/２
＝１－36×２/９
＝１－８
＝－７
（２） 70.7％
（３ａ＋ｂ）/４－（ａ－７ｂ）/８
＝｛２（３ａ＋ｂ）－（ａ－７ｂ）｝/８
＝（６ａ＋２ｂ－ａ＋７ｂ）/８
＝（５ａ＋９ｂ）/８
（３） 78.7％
（２＋√６）2
＝４＋４√６＋６
＝10＋４√６
（４） 87.3％
５ｘ－７＝９（ｘ－３）
５ｘ－７＝９ｘ－27
４ｘ＝20
ｘ＝５
（５） 88.6％
ｘ＝４ｙ＋１ …①
２ｘ－５ｙ＝８ …②
①を②に代入して、
２（４ｙ＋１）－５ｙ＝８
３ｙ＝６
ｙ＝２
①に代入、ｘ＝４×２＋１＝９
ｘ＝９、ｙ＝２
（６） 58.4％
４ｘ2＋６ｘ－１＝０
解の公式です。ｘの係数が偶数なので、ｂ＝２ｂ’が使える。
ｘ＝（－３±√13）/４
（７） 62.6％
33人の中央値（メジアン）は、（33＋１）÷２＝17番目の値。
下から足していくと４回目。
あ…４
（８） 45.6％
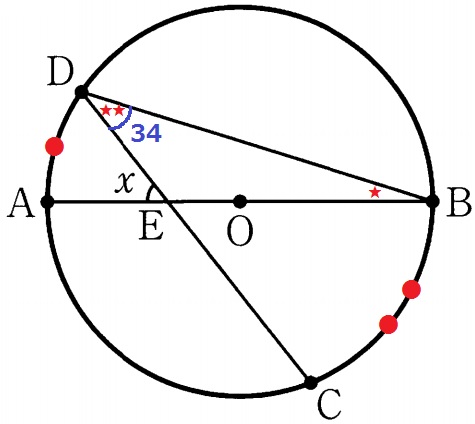
弧ＢＣ＝２×弧ＡＤより、∠ＢＤＥの半分が∠ＤＢＥである。
∠ＤＢＥ＝34÷２＝17°
△ＤＢＥで外角定理→ｘ＝34＋17＝51°
い…５、う…１
（９） 37.0％
底辺のＡＰとＢＰの長さが等しい。
ＡＢの垂直二等分線を作図し、ＡＢの中点がＰである。
大問２（式の証明）―46.6％
（１） 52.7％
手順通りに計算する。
Ｐ＝78のとき、Ｑ＝８－７＝１、Ｐ－Ｑ＝78－１＝77
Ｐ＝41のとき、Ｑ＝１－４＝－３、Ｐ－Ｑ＝41－（－３）＝44
差は77－44＝33
え…３、お…３
（２） 40.5％
これも手順通りに行えるかどうか。
まず、３桁の自然数Ｘを与えられた文字で表すと、
Ｘ＝100ａ＋10ｂ＋ｃ
Ｙは（一の位ｃ）－（十の位ｂ）＋（百の位ａ）だから、
Ｙ＝ｃ－ｂ＋ａ
11の倍数にしたいので、最終的に11でくくるようにもっていく。
Ｘ－Ｙ
＝（100ａ＋10ｂ＋ｃ）－（ｃ－ｂ＋ａ）
＝99ａ＋11ｂ
＝11（９ａ＋ｂ）
９ａ＋ｂは整数だから、11（９ａ＋ｂ）は11の倍数である。
したがって、Ｘ－Ｙの値は11の倍数になる。
＠11の倍数の判定法＠
奇数番目の位の和と偶数番目の位の和の差が11の倍数であれば、その数は11の倍数である。
ようは位を互い違いに足して両者の差が11の倍数になるか。
たとえば、【538296】の奇数番目は６＋２＋３＝11、偶数番目は９＋８＋５＝22で、
差が22－11＝11だから538296は11の倍数。
【259578】の奇数番目は８＋５＋５＝18、偶数番目は７＋９＋２＝18で、
差が０のときも11の倍数になる（11×０＝０）。
どうしてこうなるのか。専修大学松戸で出題されました。
大問３（関数）―50.6％
（１） 67.7％
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－４のとき、最大値ｙ＝４
０≦ｙ≦４
①…ウ、②…キ
（２） 69.4％
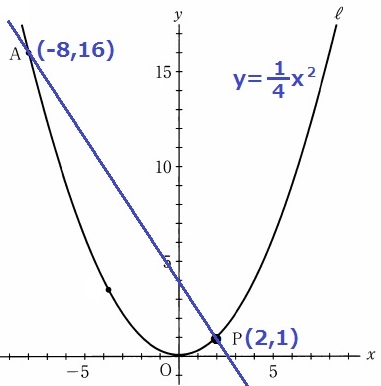
ｙ＝１/４ｘ2にｘ＝－８、２を代入して、ＡとＰの座標を確定する。
Ａ（－８、16）→Ｐ（２、１）
右に10、下に15だから、傾きは－15/10＝－３/２
Ｐから左に２、上に３移動して、切片は１＋３＝４
ＡＰ；ｙ＝－３/２ｘ＋４
③…ア、④…エ
（３） 14.7％！
求めたいＰのｘ座標をｔとする。Ｐ（ｔ、１/４ｔ2）
Ｑ（－８、１/４ｔ2）
ＲＯ；ｙ＝－２ｘ
与えられた比からＲの位置がポイントになるので、Ｒのｘ座標を求めてみる。
ここで内分点の公式を使います。
高校数学の美しい物語より。高校数学で習いますが、小技として知っておくと便利です。
ＰとＱはｙ座標が等しいので、ｘ座標だけを考える。
Ｑ（－８）とＰ（ｔ）を１：３に内分するＲのｘ座標は、
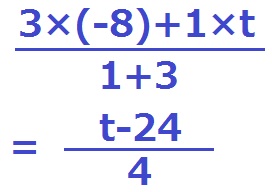
ＰＱではなく、左からＱＰとしています。分子の比は逆にかける。
（*公式を使わなくてもＱＰ＝ｔ＋８から、－８＋（ｔ＋８）×１/４＝（ｔ－24）/４でもＯＫ）
これをｙ＝－２ｘに代入して、Ｒのｙ座標は、－２×（ｔ－24）/４＝（24－ｔ）/２
Ｒのｙ座標で等式。
（24－ｔ）/２＝１/４ｔ2 ←４倍
48－２ｔ＝ｔ2
ｔ2＋２ｔ－48
＝（ｔ＋８）（ｔ－６）＝０
０＜ｔ＜８より、ｔ＝６
＠別解＠
ＱＲ：ＲＰ＝①：③を下に引き伸ばす。
ＡＰの延長線とｘ軸の交点をＳとする。
①＝８→③＝24なので、Ｓ（０、24）
Ａ（－８、16）→Ｓ（０、24）
右に８に、下に16だから、傾きは－８/16＝－１/２
Ａから右に８、下に４移動して、切片は16－４＝12
ＡＳ；ｙ＝－１/２ｘ＋12
これとｙ＝１/４ｘ2との交点がＰだから、
１/４ｘ2＝－１/２ｘ＋12
ｘ2－２ｘ＋48
＝（ｘ＋８）（ｘ－６）＝０
０＜ｘ＜８より、ｘ＝６
大問４（平面図形）―39.8％
（１） 62.2％
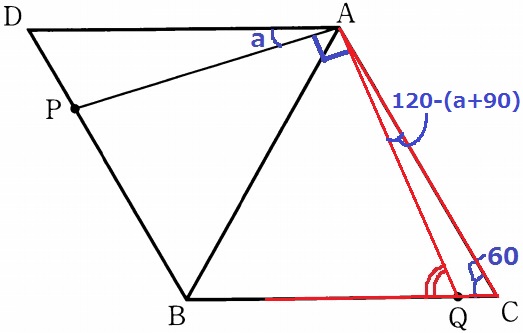
外角定理を疑う。
∠ＡＣＱ＝60°なので、∠ＱＡＣさえわかればいい。
∠ＤＡＣ＝60×２＝120°だから、∠ＱＡＣ＝120－（ａ＋90）＝30－ａ
△ＡＣＱで外角定理→∠ＡＱＢ＝（30－ａ）＋60＝90－ａ
イ
（２）① 55.0％
△ＡＢＰ≡△ＡＣＱの証明。
△ＡＢＣと△ＡＢＤは正三角形だから、
ＡＢ＝ＡＣ、∠ＡＢＰ＝ＡＣＱ
∠ＢＡＰ＝60－∠ＢＡＱ＝∠ＣＡＱ
１辺と両端角が等しいので合同。
② 2.3％!!
前問の合同から、ＱＣ＝ＰＢ＝①
ＢＱ＝③－①＝②
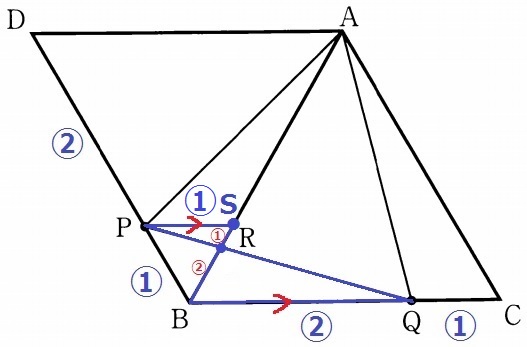
Ｐを通るＢＣに平行な線をひき、ＡＢとの交点をＳとする。
△ＢＳＰは正三角形でＰＳ＝①
△ＢＱＲ∽△ＳＰＲより、ＢＲ：ＲＳ＝②：①
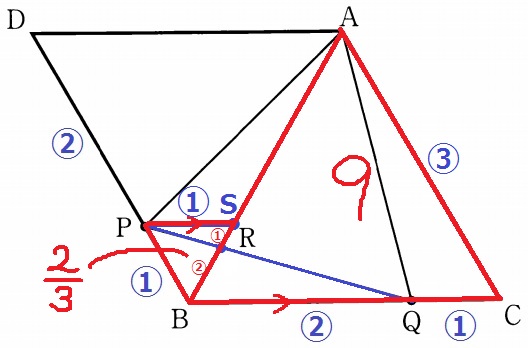
△ＡＢＣと△ＢＳＰは正三角形で相似。
△ＡＢＣの面積比は、③×③＝９
△ＢＳＰは、①×①＝１
△ＢＲＰは、１×②/③＝２/３
△ＢＲＰ：△ＡＢＣ＝２/３：９＝２：27
したがって、△ＢＲＰは△ＡＢＣの２/27倍。
か…２、き…２、く…７
大問５（空間図形）―15.6％
（１） 29.9％！
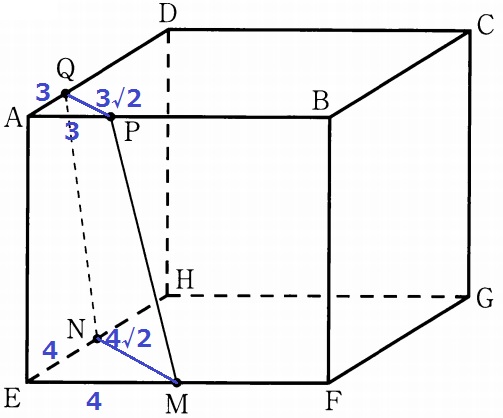
△ＡＰＱと△ＥＭＮは直角二等辺三角形。
辺の比は１：１：√２で、ＰＱ＝３√２ｃｍ、ＭＮ＝４√２ｃｍ
ＰＭは上のような直角三角形で三平方の定理を用いて５√２ｃｍ。
ＱＮも同様。
四角形ＭＰＱＮの周りの長さは、３√２＋４√２＋５√２×２＝17√２ｃｍ
け…１、こ…７、さ…２
（２） 1.2％!!!
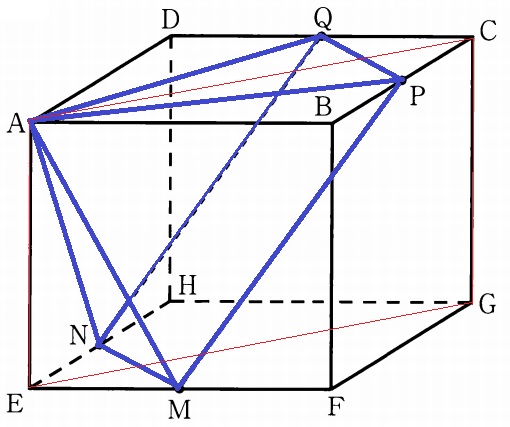
四角錘がナナメに傾いている。
長方形ＡＥＧＣで区切ると四角錘Ａ―ＭＰＱＮは左右対称に２等分される。
ＰＱとＭＮの中点をそれぞれＲ、Ｓとする。
△ＣＰＲは直角二等辺だから１：１：√２よりＣＲ＝２√２ｃｍ
同様にＡＣ＝８√２ｃｍで、ＡＲ＝８√２－２√２＝６√２ｃｍ
正面から見た図を頼りに△ＡＳＲの面積は、６√２×７÷２＝21√２ｃｍ2
（１）より、ＭＮ＝ＰＱ＝４√２ｃｍ
△ＡＳＲを底辺と見立て、断頭三角柱の考えを用いて左右一括で処理する。
高さの平均はＭＮとＰＱとＡ（０ｃｍ）の平均で、（４√２＋４√２＋０）÷３＝８√２/３ｃｍ
したがって、四角錘Ａ―ＭＰＱＮの体積は、21√２×８√２/３＝112ｃｍ3
し…１、す…１、せ…２
大問１
ここだけで配点が46点もある。失点は防ぎたい。
（２）通分時は分子のカッコを忘れずに！
（８）弧が半分になると円周角も半分。
（９）作図もとりやすかった。
大問２
（１）差の差を出す。
（２）易化。立式しやすかった。
大問３
（２）までは取りたい。
（３）求めたいＰのｘ座標を文字に置き換え、どこかで等式をつくる。
新たに登場したＲの座標に目をつけたい。
また、１：３をｘ軸まで引き伸ばすとＡのｘ座標が①になる。
大問４
（１）求めたい角で外角定理を使う場合、どことどこの角が欲しいか。
（２）①オーソドックスな証明。
②いろんなやり方がある。
解説では△ＡＢＣが１辺③の正三角形だから、１辺①の正三角形をつくって△ＢＲＰを求めた。
大問５
（２）ゴリゴリのテクニックを使ってしまった:( ´ω` ):
対称面を底面とみなす断頭三角柱は幅広く使える。
ラストのスクリーン問題の別解にて、同じテクニックを駆使しています。
こちらは断頭を前提にした設問です。
＠2022年度・都立解説＠
数学(分割後期) 社会…平均49.2点 理科…平均61.4点 英語…平均61.1点
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント