問題PDF
(4)
縦40cm、横64cmの長方形の紙2枚をそれぞれ4cmずつの幅に切り、
これをつないで長いテープを作ります。
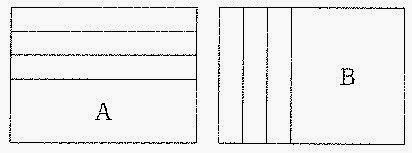
1枚目はAのように切って、のりしろを1cmずつにしたテープを作りました。
2枚目はBのように切って、のりしろを( )cmずつにしたテープを作ったところ、
2本のテープの長さは同じになりました。
(6)
太郎君は旅行を計画しました。
全体の予算の3/5を交通費にして、実際に旅行に行ったところ、
交通費は予定の4/3倍かかり、その他の費用は予定より2100円少なくすみました。
その結果、全体の費用は予算の9/8倍になりました。はじめの予算は( )円です。
(7)
図のように、直線上の点Aを中心にして半径3cmの円をかき、
Aの右側で直線と交わった点をBとします。次にBを中心にして同じ半径の円をかき、
Bの右側で直線と交わった点をCとしてこの作業を繰り返します。
円を20個かいたときにできる図形の周の長さは( )cmです。

(8)
ある果物屋さんで、下の表にA、B、Cのつめ合わせを合計40セット作ります。

りんご216個、もも129個、みかん203個を余ることなくつめ合わせると、
Aは( )セット、Bは( )セット、Cは( )セット作れます。
(9)
花子さんは、いくつかのテストを受けたところ、全教科の平均点は72点で、
算数以外の教科の平均点は全教科の平均点より1.75点低く、
国語以外の教科の平均点は全教科の平均点より1.25点高くなりました。
国語と算数の点数の差が24点のとき、算数は( )点です。
(10)
長方形ABCDがあります。
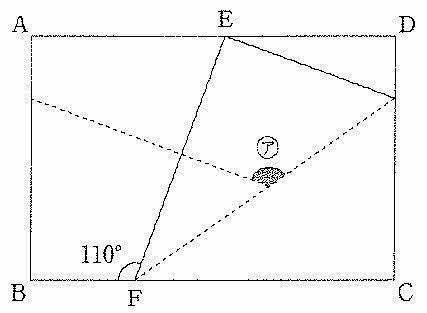
図のように、頂点Cを辺AD上に点Eに合わせて折り、
さらに点Fを点Eに合わせて折りました。アの角度は( )度です。
(12)
長方形ABCDがあります。
図のように、三角形ACDを頂点Cを中心に45度回転して三角形ECFに移動しました。
色のついた部分の面積は( )cm2です。

(14)
ひろ子さんとまさお君の2人は50mのプールの両端から同時に泳ぎだし、
何度か往復してそれぞれ1500m泳ぎました。
ひろ子さんとまさお君は何回かすれ違いますが、
2回目にすれ違ったのはひろ子さんが1度目に折り返してから20m進んだ位置でした。
ただし、2人の泳ぐ速さはそれぞれ一定です。
①1回目に2人がすれ違ったのは、ひろ子さんが泳ぎ始めて( )mのところです。
②2人が最後にすれ違ったのは、まさお君が泳ぎ終わる( )m手前です。
@解説@
(4)
横に切ると、テープは40÷4=10枚できる。
のりしろがない場合を想定した全長から、のりしろ部分の合計を引く。
64×10-1×(10-1)=631cm
縦に切ると、テープは64÷4=16枚できる。
同様に考えて、40×16-□×(16-1)=631
□=3/5cm
(6)
線分図で情報整理。

はじめの予算を⑤とおくと、予定の交通費は③、実際の交通費は④。
実際の交通費は、③×4/3=④、その他の費用は②-2100円。
実際にかかった費用の合計は、⑤×9/8=○45/8
○45/8=④+②-2100
○3/8=2100
⑤=2100×⑤ / (○3/8)=28000円
(7)
2019年の都立入試でほぼ同じものが出ております。
正答率は5.2%で、無解答が7割を超えている…。

半径を頼りに正三角形が見つかる。
両端の中心角は240°、あいだの弧の中心角は上下60°
気をつけるべき点は、60°の弧は上下で18組あること!
3個目の円で1組の弧が上下にできる。
植木算のように-1ではなく、20-2=18個である。
3×2×3.14×(240×2+60×2×18)/360
=138.16cm
@@@
ちなみに、都立入試に出た式を当てはめてみると、
1つの円の円周の長さℓ=3×2×3.14=18.84cm
円の数n=20個。周りの長さMは、
M=1/3ℓ(n+2)=1/3×18.84×(20+2)=138.16cm
(8)
文字式を使います。
小学生に教えるときは、○・△・×に置き換えてください。

Aセットをx、Bセットをy、Cセットをzとする。
x+y+z=40 …①
7x+3y+5z=216 …②
4x+3y+2z=129 …③
3x+6y+8z=203 …④
②-③
7x+3y+5z=216
-)4x+3y+2z=129
3x +3z=87 …⑤
x+z=29
①より、y=40-29=11
yの係数が大きい④に代入。
3x+6×11+8z=203
3x+8z=137 …⑥
⑥-⑤
3x+8z=137
-)3x+3z=87
5z =50
z=10
x=40-11-10=19
よって、Aは19セット、Bは11セット、Cは10セット。
(9)
全教科が何科目かは不明。
算数を除くと平均が下がり、国語を除くと平均が上がるということは、
花子は算数が得意で、算数の方が国語より得点が高い。
算数=国語+24点
算数以外の平均と国語以外の平均の差は、1.75+1.25=3点
算国で24点差あり、いずれかを抜かした平均で3点差がでるということは、
いずれか1つを抜かした科目数は、24÷3=8科目ある。
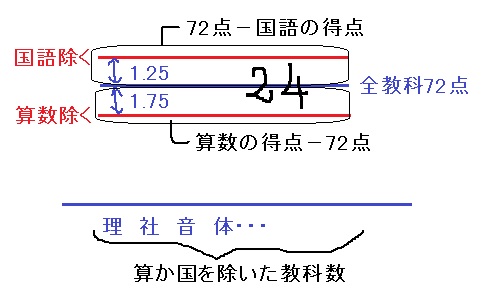
全平均72点より高かった算数の得点を算数以外で均すと下の枠線となり、
全平均72点より低かった国語の点数を国語以外で均すと上の枠線となる。
72点より下の1.75点を8科目でかけ合わせて72点に足すと算数の得点。
算数の得点は、72+1.75×8=86点
(10)

折り返しより、∠EFH=(180-110)÷2=35°
2回目の折り目を対称の軸とすると、EとFが対応する。
EG=FGで△EFGは二等辺三角形。
∠GEF=35°
△EFGの内角から、●=(180-35×2)÷2=55°
ア=180-55=125°
@別解@
対称の軸とEFは垂直に交わるので、
外角定理を使って、35+90=125°でもいけました。
(12)

DC→FCと45°回転移動。∠DCF=45°
∠FCG=90-45=45°
△FCGは90°-45°-45°で直角二等辺となる。
FG=FC=10cm
EG=24-10=14cm
求積すべきところは、半径26cm、中心角45°の扇形ACEから、
△ABCと△CEGをひけばいい。
△CEGの面積は、△CEFをEF:EGの比で按分する。
26×26×3.14×45/360-24×10÷2-24×10÷2×14/24
=236.33-120-70=75.33cm2
(14)①
各々の速さは不明だが、距離の比から速さの比が出る。
2回目までのすれ違いを線分図で確認。
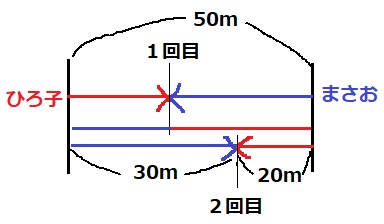
赤い矢印がひろ子、青い矢印がまさお。
2回目までのすれ違いまで、ひろ子は70m、まさおは80m泳ぐ。
速さの比は、ひろ子:まさお=70:80=7:8
1回目のすれ違いまでに泳ぐ距離も、ひろ子:まさお=7:8
よって、1回目のすれ違いまでにひろ子が泳ぐ距離は、
50×7/15=70/3m
②
まさおが1500mを泳ぎきったとき、ひろ子は1500×7/8=1312.5m泳いでいる。

1312.5m=50×26+12.5m
つまり、ひろ子は50mプールを26回(往復で13回)泳ぎ、スタートから12.5mのところにいる。
上の状態から逆再生して、最後のすれ違いまでさかのぼる。
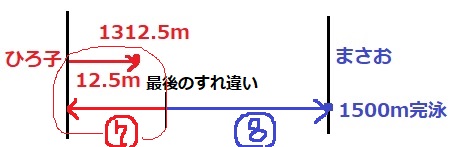
最後のすれ違いからの距離も、ひろ子:まさお=⑦:⑧
⑦+⑧=⑮=50+12.5=62.5m
したがって、62.5×⑧/⑮=100/3m



コメント