問題PDF
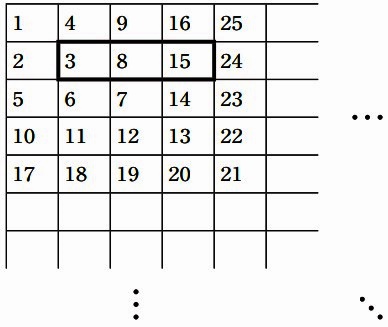
表のように、あるきまりにしたがって整数が1から順に並んでいます。
上からx番目、左からy番目の位置にある数を(x、y)と表すことにします。
例えば、(2、3)=8です。このとき、次の問いに答えなさい。
(1) 得点率63.1%
次の〔 ア 〕、〔 イ 〕にあてはまる数を答えなさい。
(10、9)=〔 ア 〕
(7、7)+(7、8)=〔 イ 〕
(2) 得点率30.1%
次の〔 ウ 〕、〔 エ 〕に入る数は、どのような数ですか。
①~⑥のうち、正しい組み合わせを選びなさい。
(2022、10)+(2022、11)+(2022、12)=〔 ウ 〕
(2022、2021)+(2022、2022)+(2022、2023)=〔 エ 〕

(3) 得点率6.0%
表の太枠にある3つの数3、8、15の和は26です。
このように横に並んでいる3つの数の和が404となるとき、3つの数をすべて答えなさい。
なお、この問題は解答までの考え方を表す式や文章・図などを書きなさい。
@解説@
(1)
xとyを取り違えないこと!
上からx番目、左からy番目なので、xが横の行、yが縦の列。
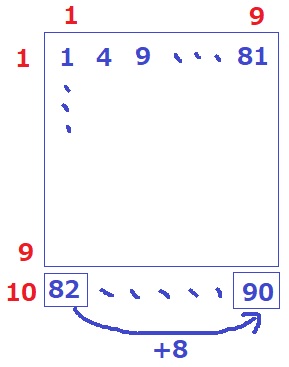
平方数が1行目に並ぶ。(1、9)が81。
次の(10、1)が82。(10、9)は横に8だから、ア=82+8=90
*あいだの数なので+8。+9ではない。
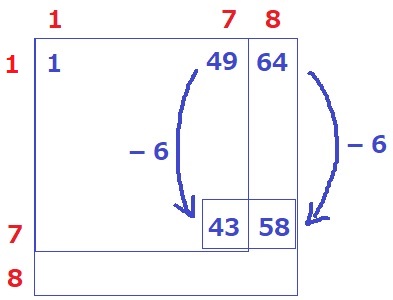
(1、7)が49、(1、8)が64。
7行目だからこれらの6個下。
イ=(49-6)+(64-6)=101
ア…90、イ…101
(2)
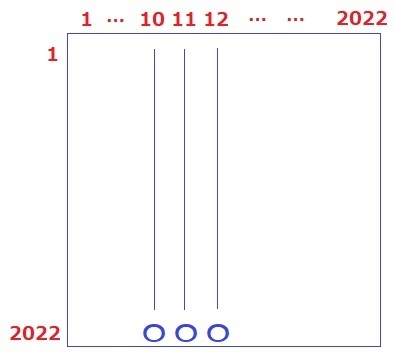
連続する3つの整数の和である。
最初の数を●とすると、●+(●+1)+(●+2)=●×3+3=3×(●+1)
3の倍数だから3で割り切れる数。
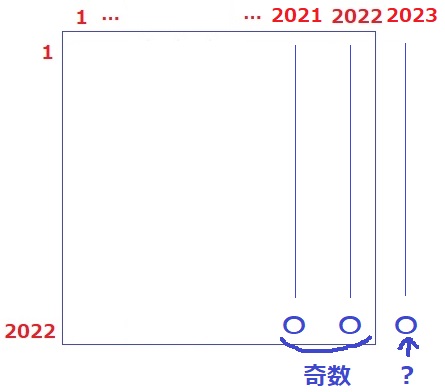
最初の2つは連続する整数なので和は奇数。
問題は右の数だけ正方形から外れる(;´Д`)
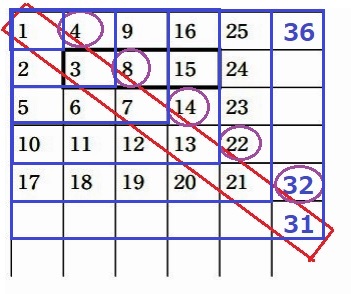
表を観察すると、正方形の右下の数(赤線)の1個右の数をみると、
4・8・14・22・32…といずれも偶数である。
したがって、奇数と偶数の和で答えは奇数となる。
②
@余談@
なぜ右端が偶数となったのか、これも平方数が出発点である。
偶数列目…偶数×偶数-偶数=偶数-偶数=偶数
e.g.)4×4-2=14
奇数列目…奇数×奇数-奇数=奇数-奇数=偶数
e.g)5×5-3=22
(3)
横に並ぶ3つの数字には3パターンある。
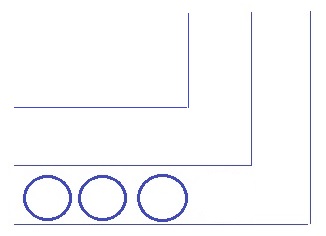
まず、同じ正方形に横並びするパターン。
連続する3つの整数だから、前問より和が3の倍数になる。
404は3の倍数ではないから×!
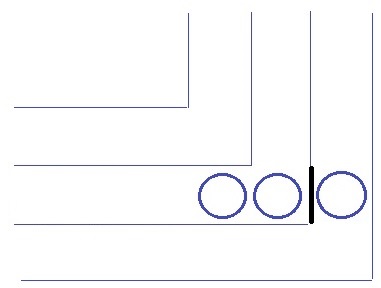
右1つだけが違う正方形にあるパターン。
前問より奇数になるので404は×!
となると、これしかない。
すなわち、3つの数がそれぞれ別の正方形にある。
本問の特徴的な数は平方数なので、平方数から活路を見出す。
404÷3=134…2
【…100・121・144・169…】と平方数を並べてみると、
100+121+144=365
121+144+169=434
↑これが404より大きい数のうち、最も404に近い。
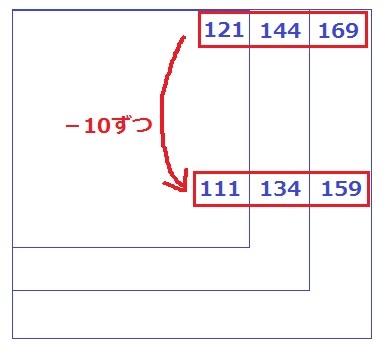
差は434-404=30
それぞれを-10する。答えは111と134と159。




コメント