2019年度　サレジオ学院中学過去問【算数】大問５解説

問題ＰＤＦ
ある小学校の授業で、次の新聞記事が取り上げられました。
授業における先生と生徒たちとの会話文を読んで、次の問いに答えなさい。

（先生）：どうやらプラスチックごみの増加が問題になっているようです。記事には、2050年の発生量の予測が書かれてあります。空欄にはどんな数字が入ると思いますか。
（かい君）：記事にあるグラフをみると、2000年から2005年までの５年間のごみの量が約0.5億トン増えていて、2005年から2010年までの５年間でも、同じように約0.5億トン増えています。だから、このまま５年間で0.5億トンずつ増えていくと考えれば、2050年には、〔　ア　〕トンになると思います。
（先生）：なるほど。そういう見方もありますね。他に意見はありますか。
（りく君）：グラフをみると、1980年から2000年までの20年間でごみの量は約３倍になっています。この割合で増えると考えれば、2020年には2000年の３倍の約4.5億トンになると思います。そして、同じように考えれば、2000年からの50年間で約〔　イ　〕倍になると考えられるので、2050年のごみの量は、約〔　ウ　〕億トンになると思います。
（先生）：うーん、たしかに。これはかい君と異なる新しい見方ですね。２人とも意見を出してくれてありがとう。ただ、実際は、この記事の空欄には、２人の予想を大きく上回る120という数字が入っていました。どうしてそうなるのでしょうか。引き続き、もっといろんな角度からこの問題について考えていきましょう。

（１）
かい君の予測は、「５年間で0.5億トンずつ増えていく」という考え方をもとにしています。
このとき、〔　ア　〕に入る数を答えなさい。

（２）
りく君の予測は、「20年で３倍になる」という考え方をもとにしています。
このとき、〔　イ　〕〔　ウ　〕に入る数の組合せとしてもっとも適切なものを選びなさい。
また、その理由も答えなさい。
①イ：3.5　ウ：5.25
②イ：7.5　ウ：11.25
③イ：13.5  ウ：20.25
④イ：15.6  ウ：23.4
⑤イ：21.6  ウ：32.4

（３）会話文にある２人の予測は、記事にある予測と比べてとても小さい数字でした。
その理由として適切なものを次の中から２つ選びなさい。
①世界の人口増加やプラスチックの使用量の増加など、他にも考えるべき要因があるから。
②プラスチックごみのリサイクル率が上がり、ごみの発生量は減少していくと考えられるから。
③２人の考え方が成り立たない年代があるから。
④レジ袋などの使い捨て製品の有料化が進むから。
⑤プラスチックに替わる新しい材料が開発されるから。

（２）
『20年で３倍』
1980年－0.5億トン
2000年－1.5億トン
2020年－4.5億トン（2000年基準で３倍）
2040年－13.5億トン（９倍）
2060年－40.5億トン（27倍）
2050年は９倍より大きく、27倍より小さいので、①と②は×。

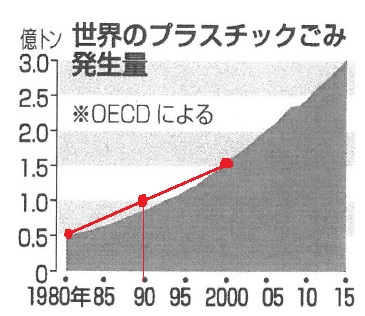
1980～2000年を直線でひくと、真ん中の1990年は半分の1.0億トンより下。
このように考えると2050年は、（13.5億＋40.5億）÷２＝27億トンより下になるはず。
③・④に絞られる。

2000年からスタートすると2050年が出せないので、2010年から考える。
かい君のセリフから、2010年は2.5億トンとする。
2010年－2.5億トン
2030年－7.5億トン
2050年－22.5億トン
りく君は2020年を4.5億と予測したので、22.5÷4.5＝15倍
これに近い組み合わせは④となる。

（３）
かい君は6.5億トン、りく君は22.5億トンと予測したが、
記事に書かれていた2050年度のプらごみ予測は約120億と書かれていた。
②・④・⑤はむしろプラごみを減少させるので、消去法で①・③と出てしまう。
①人口増加やプラスチック使用量の増加など、別の原因が発生した。
③２人の考え方が通用しなくなった。

2018年のＧ７サミットでは、プラスチックごみ削減を盛り込んだ「海洋プラスチック憲章」につき、イギリス・フランス・ドイツ・イタリア・カナダ・ＥＵは署名したが、日本とアメリカは財界からの反対を理由に署名しなかった。海に流れたプラスチックは波や紫外線で砕け、マイクロプラスチックとして海を漂う。それを魚が飲み込むと、生物濃縮により生態系や人体への悪影響が懸念される。マクドナルドやスターバックスは使い捨てのプラスチック製ストローの使用を段階的に廃止する方針を打ち出し、レジ袋有料化の声も上がっている。
社会科の時事で問われるので、概要は把握しておきましょう。

■追記■
2020年７月１日より、レジ袋有料化start！
難関中（算数科）解説ページに戻る