問題ＰＤＦ
（１）
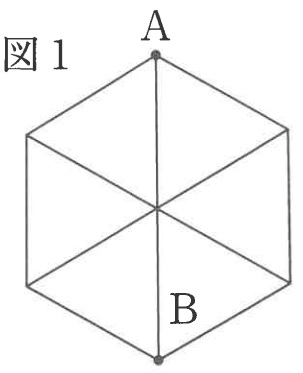
図１は１本の長さが１ｃｍの線分12本で作られる図形です。
線分を通り、点Ａから点Ｂへ行く道のりについて考えます。
ただし、一度点Ｂに到着したらその道のりは終わること、
途中で点Ａに戻る道のりは考えないことにします。
（あ）
同じ点も同じ線分も２度は通らないとすると、
最も長い道のりは何ｃｍになりますか。
（い）
点Ａ、Ｂ以外の点は何度通ってもよいですが、同じ線分は通らないとすると、
最も長い道のりは何ｃｍになりますか。
（２）
図２のような道があります。
海君と陽子さんは同時に出発し、二人とも同じ速さで、
遠回りせずに目的地まで道を歩きます。
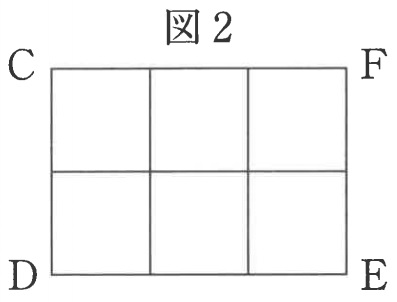
（う）
海君がＤからＦまで歩く歩き方は何通りありますか。
（え）
海君がＤからＦまで歩き、陽子さんはＥからＣまで歩きます。
海君と陽子さんが出会う歩き方は何組ありますか。
（お）
海君がＤからＦまで、陽子さんがＦからＤまで歩くとき、
海君と陽子さんが出会わない歩き方は何組ありますか。
＠解説＠
（１）（あ）
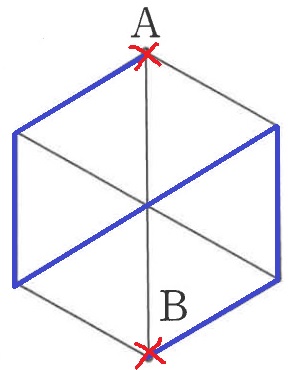
ＡとＢを避けるように遠回りする。
６ｃｍ
（い）
１手目で試しに左ルートをいくと、最大で７ｃｍ。
対称性から右ルートも同様。
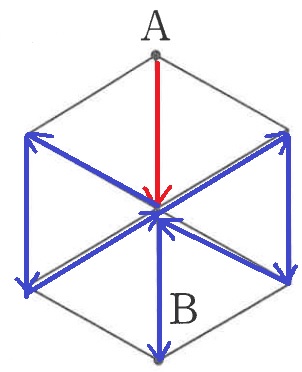
真ん中ルートでいくと８ｃｍ。
最も長い道のりは８ｃｍ。
（２）（う）
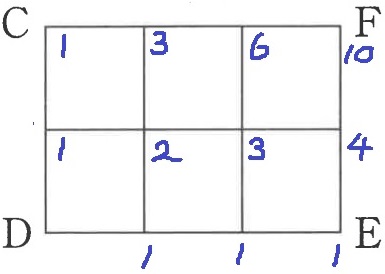
おなじみの方法。
左と下を足していって10通り。
（え）
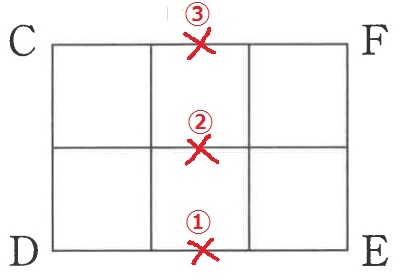
海はＤ⇒Ｆ、陽子はＥ⇒Ｃを歩く。
出発地点のＤとＥから等距離にある地点①～③で出会う。
①を通る場合、海は３通り、陽子も３通り。
３×３＝９通り
③を通る場合も同様で９通り。
②を通る場合、海…２×２＝４通り、陽子…２×２＝４通り
４×４＝16通り
よって、９＋９＋16＝34組
（お）
２人の歩き方は全体で、10×10＝100通り
前問のように出会う歩き方を出してから、余事象で出会わない歩き方を算出する。
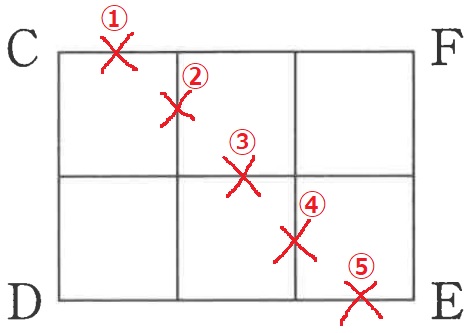
海はＤ⇒Ｆ、陽子はＦ⇒Ｄを歩く。
ＤとＦから等距離にある地点①～⑤で出会う。
①・⑤…１×１＝１通り
②・④…２×２＝４通り
③…４×４＝16通り
１×２＋４×２＋16＝26通り
したがって、100－26＝74組
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント