2019年度　芝中学過去問【算数】大問６解説

問題ＰＤＦ
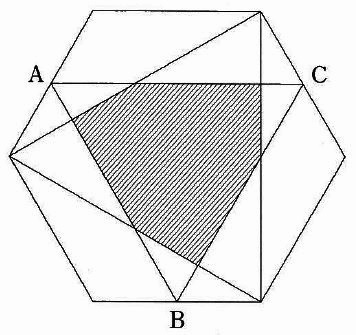
面積が96ｃｍ²の正六角形があり、３点Ａ、Ｂ、Ｃは各辺の真ん中の点です。

（１）
三角形ＡＢＣの面積は〔　　　〕ｃｍ²です。

（２）
影を付けた部分の面積は〔　　　〕ｃｍ²です。

＠解説＠
（１）

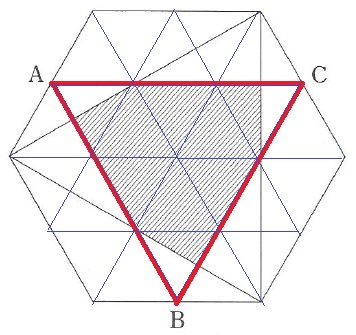
上のように分割する。
正六角形の対角線３本、ＡＣのように中点同士を６本結ぶと、
全体の正六角形が24分割される。
△ＡＢＣは９マス分なので、96×９/24＝36ｃｍ²

（２）

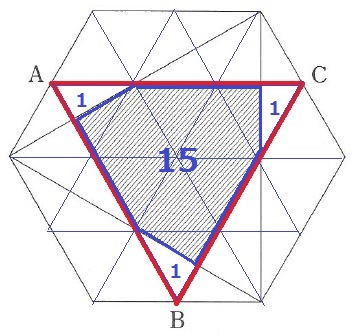
１つの正三角形を２とすると、正三角形ＡＢＣは２×９＝18
斜線部分は、18－３＝15
36×15/18＝30ｃｍ²

＠＠
この形、どこかで見たことあるなぁと調べてみたら、
今年度の滋賀県公立高校入試で同じものが出されていました。

2019年度　滋賀県公立高校入試問題過去問【数学】解説

平均38.1点問題はコチラ→リセマムさん大問１（小問集合）（１）　84.5％１５－１９＝－４（２）　73.5％１/４ａ－５/６ａ＋ａ＝５/１２ａ（３）　80.8％連立方程式。代入法でもやりやすいかな？ｘ＝３、ｙ＝－２（４）　78.8％√２７...

sabotensabo.com

2019.03.18

↑大問４のラストです。

反時計回りに30°まわせばピッタリ！
滋賀では、ＰがＢＦの中点にくる証明が①で出題されています。
ＢＥに補助線をひき、ＳとＵは中点だからＡＳ：ＳＢ＝ＦＵ：ＵＥ
平行線と線分の比から、ＡＦ//ＳＵ//ＢＥ
△ＡＢＦに注目すると、ＢＰ：ＰＦ＝ＢＳ：ＳＡ＝１：１→ＰはＢＦの中点
正答率は1.1％、難しかったです。
斜線部分の面積を求める③は0.7％でした。
難関中（算数科）解説ページに戻る