2019年度　岩手県公立高校入試問題過去問【数学】解説

平均45.1点
問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）
－２－５＝－７

（２）
８（３/４ａ＋１）
＝８×３/４ａ＋８×１
＝６ａ＋８

（３）
（３－√２）²
＝９－６√２＋２
＝11－６√２

（４）
ｘ²－10ｘ＋24
＝（ｘ－６）（ｘ－４）

（５）
３ｘ²－５ｘ＋１＝０
因数分解ができないので、解の公式を適用。
ｘ＝（５±√13）/６

大問２（等式の変形）

Ｖ＝１/３Ｓｈ
３Ｖ＝Ｓｈ
ｈ＝３Ｖ/Ｓ

大問３（反比例）

「加熱時間は電子レンジの出力に反比例する」
反比例の一般式：ｙ＝ａ/ｘ
ａ＝500Ｗ×240秒
よって、800Ｗでの加熱時間は、500×240÷800＝150秒

大問４（平面図形）

（１）
角の二等分線の作図。
①Ｏから適当な弧を描く。
②その弧とＯＡ、ＯＢとの交点からそれぞれ適当な弧を描く。
③②の交点とＯをひく。

（２）

円周角の定理から、∠ＡＯＢ＝70×２＝140°
半径と接線は垂直の関係。
四角形ＡＯＢＰの内角で90°が２つある。
残りの２角から、∠ＡＰＢ＝180－140＝40°

（３）

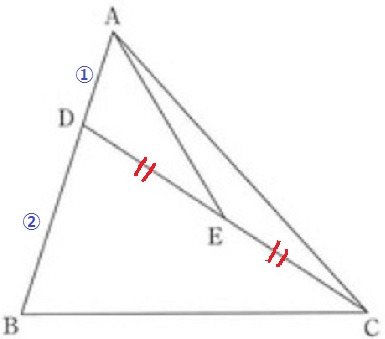
△ＡＢＣの面積を１として、△ＡＢＣ⇒△ＡＤＣ⇒△ＡＥＣの順で計算。
△ＡＥＣ＝１×１/３×１/２＝１/６
△ＡＢＣ：△ＡＥＣ＝１：１/６＝６：１

大問５（方程式）

『用いる文字が何を表すか』も自分で示さなくてはならない。
ポイントは、先に１ｇあたりのカロリーを算出しておくこと。
１ｇあたりのカロリーが異なるので、そのまま式に採用できない。

・ほうれん草…54kcal÷270ｇ＝0.2kcal/ｇ
・ごま…60kcal÷10ｇ＝６kcal/ｇ

ほうれん草をｘｇ使うとする。ごまの使用量は83－ｘｇ。
カロリーで等式を作成する。
0.2ｘ＋６（83－ｘ）＝63
5.8ｘ＝435
ｘ＝75
ほうれん草…75ｇ、ごま…８ｇ

大問６（データの活用）

８人の中央値（メジアン）→４番目と５番目の平均値
４番目…34　５番目…36
その平均値なので35ｋｇ

大問７（確率）

（１）
サイコロの出目は１～６。
２回振って和が８になる組み合わせを調べる。
〔２・６〕〔６・２〕〔３・５〕〔５・３〕〔４・４〕
このうち、〔２・６〕以外の４通りが正解。

（２）
丁寧に調べる必要がある。
■１回目に１
ゴールまで残り７マスだが、２回目に６を出せば７マス目でもう１マス進めてゴール。
■１回目に２
２マス戻るとゴールまで８マス。７マス目まで届かず、ゴール不可。
■１回目に３
３を出して７マス目まで行き、そこから１マス進んでゴール。
４を出してストレートにゴール。
５を出してゴールから１つ戻り、７マス目で１マス進んでゴール。
■１回目に４
１回休憩なので、２回でゴール到達不可。
■１回目に５
２・３・４を出せばゴール。
■１回目に６
１・２・３を出せばゴール。
⇒計10通り。

理由の記述は、条件前と条件後の確率を並べて比較すればＯＫ。
条件前のゴール到達確率→５/36
条件後のゴール到達確率→10/36＝５/18
サイコロを２回振ってゴールする確率は、条件が追加された後の方が２倍大きいので、
さくらの考えは正しいとはいえない。

大問８（図形の証明）

△ＡＢＦ∽△ＧＥＢの証明。

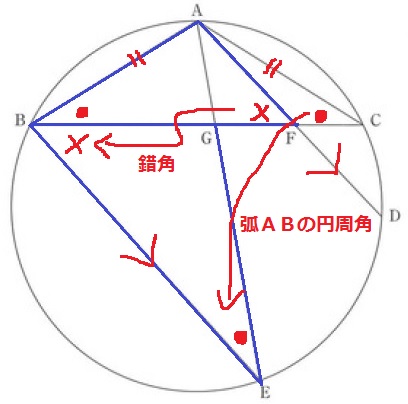
●…△ＡＢＣが二等辺で底角が等しい。これを弧ＡＢに対する円周角とコンボ。
×…ＡＤ//ＢＥで錯角。
以上、２角が等しく∽。

大問９（数量変化）

（１）
列車は７分で７ｋｍ進む→分速１ｋｍ。

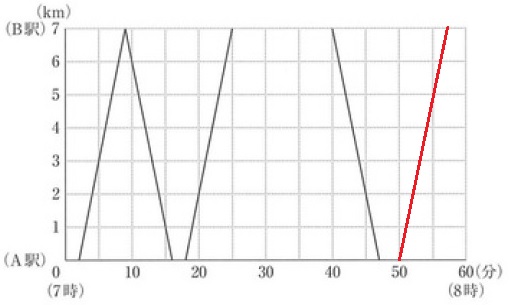
７：50から出発。
線をひくときは格子点を意識しよう！
７：55にＡ駅から５ｋｍ地点を通過する。

（２）
列車に２回追い越され、１回すれ違う。

はるとがＢ駅に25分以上40分未満で着けばいい。
40分を超えてＢ駅に着くと、２回目のすれ違いが起こる。
25分以下でＢ駅に着くと、２回目の追い越しが起きない。

７ｋｍを25分⇒７×60/25＝時速16.8ｋｍ
７ｋｍを40分⇒７×60/40＝時速10.5ｋｍ
したがって、時速10.5ｋｍ以上、時速16.8ｋｍ未満。

大問10（関数）

（１）
最小値…ｘ＝０のとき、ｙ＝０
最大値…ｘ＝６のとき、ｙ＝９
０≦ｙ≦９

（２）
Ａ座標を（ｓ、１/４ｓ²）とおく。

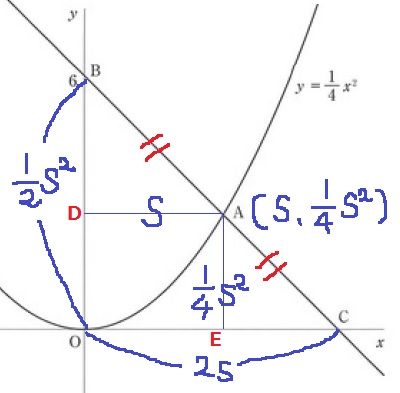
Ａからｘ軸とｙ軸に向けて垂線。交点をＤ・Ｅとする。
△ＢＡＤ∽△ＢＣＯ、△ＡＣＥ∽△ＢＣＯから、
ＤとＥはそれぞれＢＯ、ＣＯの中点にある。

ＢＯ＝１/４ｓ²×２＝１/２ｓ²＝６
ｓ＞０より、ｓ＝２√３
ＣＯ＝２ｓ＝２×２√３＝４√３
よって、Ｃ（４√３、０）

大問11（空間図形）

（１）
△ＡＢＰで三平方→ＡＰ＝√（７²＋１²）＝５√２ｃｍ

（２）
菱形の面積＝対角線×対角線÷２

ＡＣは直方体の対角線。
*１辺の長さがａ、ｂ、ｃである直方体の対角線→√（ａ²＋ｂ²＋ｃ²）
（他の都道府県でもよく出ましたよ！）

ＡＣ＝√（７²＋５²＋６²）＝√110ｃｍ

ＰＱを対角線とする直方体を作成。
ＰＱ＝√（７²＋５²＋４²）＝√90＝３√10ｃｍ
したがって、菱形ＡＰＧＱの面積は、√110×３√10÷２＝15√11ｃｍ²

大問12（不定方程式）

（１）
不定方程式。（埼玉・岐阜でも出題）
２ｘ＋３ｙ＝８
ｙで場合分けしてもいい。
（４、０）（１、２）

＠別解＠
定数が整数になるよう、ｘについて解く。
２ｘ＝－３ｙ＋８
ｘ＝－３/２ｙ＋４
ｙが整数となるのは偶数だけ。
ｘが整数になる数値を調べていく。

（２）ア
２ｘ＋３ｙ＝12
係数が３であるｙで場合分けすると、
（ｘ、ｙ）＝（６、０）（３、２）（０、４）

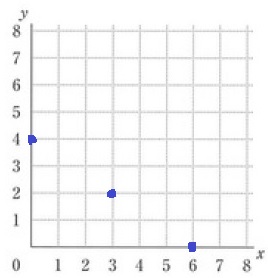
そのままプロット。

イ
ｘとｙの値をできるだけ近くする。
２ｘ＋３ｙ＝７　（２、１）
２ｘ＋３ｙ＝８　（１、２）
２ｘ＋３ｙ＝９　（３、１）
２ｘ＋３ｙ＝10　（２、２）
２ｘ＋３ｙ＝11　（１、３）

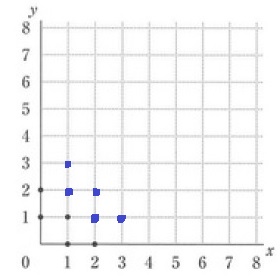
同様にプロットする。

＠＠＠
係数が１つ違いなので、２と３の個数をうまく組み合わせれば、あらゆる整数が作れる。
ちなみに、続きを書くとこんな感じになる↓

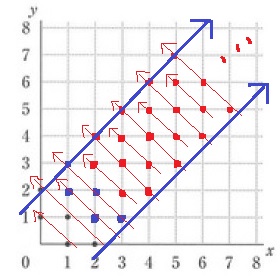
青い矢印の範囲内で左上に２コ、３コ繰り返しながら、全体では右上に向かう。
公立高校入試解説ページに戻る