2024年度　島根県公立高校入試問題過去問【数学】解説

平均26.8点（前年比；＋0.5点）

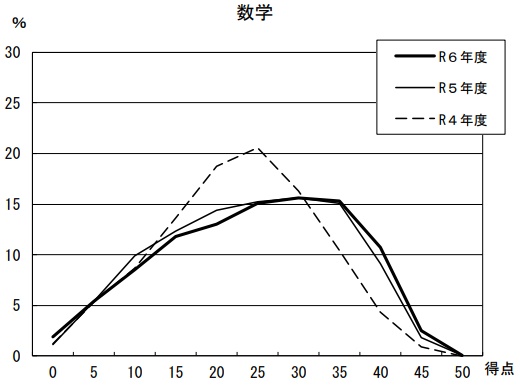
最高点―50点、最低点―０点
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
５＋３×（－４）
＝５－12
＝－７

（２）
（２√３－√７）（２√３＋√７）
＝（２√３）²－（√７）²
＝12－７
＝５

（３）
ｘ：（ｘ－３）＝５：３
内項と外項の積で、５（ｘ－３）＝３ｘ
２ｘ＝15
ｘ＝15/２

（４）
２ｘ＋３ｙ＝１　…①
ｘ－ｙ＝３　…②
①－②×２をすると、５ｙ＝－５
ｙ＝－１
②に代入。ｘ－（－１）＝３
ｘ＝２
ｘ＝２、ｙ＝－１

（５）
（ｘ－２）²＝７
ｘ－２＝±√７
ｘ＝２±√７

（６）①
毎分ｘＬでｙ分間いれると20Ｌになる。
ｘｙ＝20（ｙ＝20/ｘ）

②
30ｍから５ａｍを切った残りはｂｍより長い。
30－５ａ＞ｂ

（７）

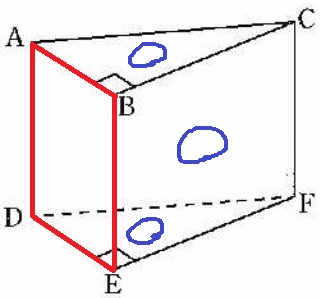
∠ＡＢＣ（∠ＤＥＦ）＝90°→面ＡＤＥＢ⊥ＢＣ（ＥＦ）→面ＡＤＥＢ⊥面ＢＥＦＣ
三角柱は側面に対して底面（△ＤＥＦ）、天井（△ＡＢＣ）は垂直。
ア・イ・エ
＠＠
厳密にいうと斜めの柱体もある。側面は長方形ではなく、平行四辺形になる。

（８）

半円の弧に対する円周角より、∠ＡＤＢ＝90°
△ＡＢＤの内角から、ｘ＝180－（90＋34）＝56°

（９）①

ＯＣを対称の軸とすると、アと線対称なのはエ。

②

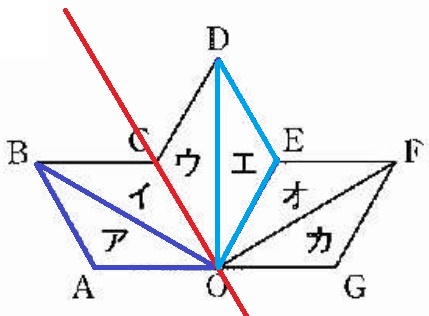
Oを回転の中心とすると、アの回転移動で重なるのはウ・オ。

大問２（データの活用・数量変化）

（１）①
累積度数…その階級までの度数の合計。
２＋10＋15＝27人

②〔１〕

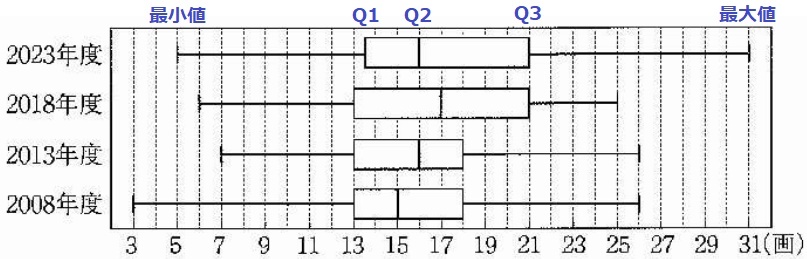
ア：2023年と2018年が共通するのは第３四分位数（Q3）。×
イ：範囲＝最大値－最小値、四分位範囲＝Q3－Q1（箱の長さ）
いずれも2013年より2023年の方が大きい。〇
ウ：平均値を×印などで示す箱ひげ図もあるが、本問にはない。×
エ：2013年の最小値は７画。×
オ：40人の中央値（Q2）は20番目と21番目の平均。
Q2がいずれも15画以上→少なくとも半数（上位20名）は15画以上。〇
イ・オ

〔２〕

最小値が３画である2008年はウ。
2013年と2018年はQ3が大きく違う。
40人のQ3は上から10番目と11番目の平均→2018年はイ、2013年はア。
ア

（２）①
100個で12000円だから、１個は12000÷100＝120円

②〔１〕

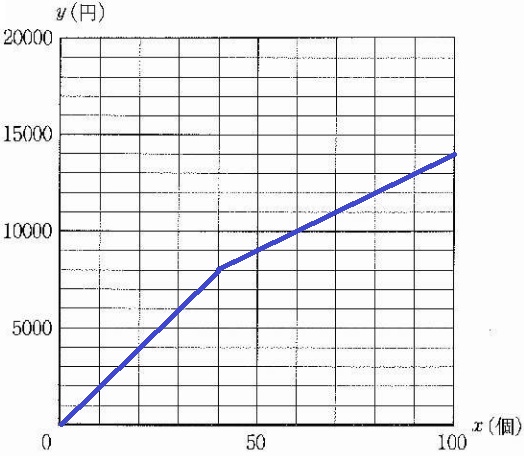
ｘ＝40のとき、ｙ＝200×40＝8000
残り60個の販売額の合計は、（200－100）×60＝6000
ｘ＝100のとき、ｙ＝8000＋6000＝14000
原点→（40、8000）→（100、14000）を結ぶ。

〔２〕

すべて200円で売ったら赤線になる。
6000円少ない。

〔３〕

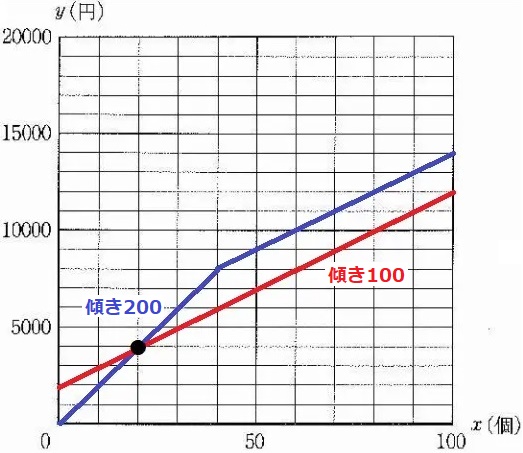
100円で売る場合、後半の傾き100と平行のグラフになる。
『販売額の合計を12000円以上にする』→（100、12000）を通る傾き100のグラフ（赤線）を描く。
交点の20個で200円から100円に値下げすれば、販売額は12000円になる。
20個以上

大問３（確率・整数）

（１）①
Ａは３枚中１枚→確率は１/３

②〔１〕
●太郎：１²＝１点
花子：２×３＝６点→花子の勝ち！
●太郎：２²＝４点
花子：１×３→太郎の勝ち！
●太郎が３点→太郎の勝ち！
太郎が勝つ確率は２/３

〔２〕
同様に調べると、花子が勝つのは太郎が１を引いたときだけ。
（２で引き分け、４で花子負け）
確率は１/３

③
（１、２、４）の場合、それぞれ勝ち１、負け１、引き分け１パターンに分かれた。
太郎が真ん中を引いて引き分けになれば、勝ち負けが１パターンずつで同じになる。
ＡＣ＝Ｂ²が成り立つ組み合わせを書けばいい。
（１、３、９）（１、４、16）（２、４、８）（１、５、25）（４、６、９）など

（２）①ア
ａ＝１（連続する整数）のとき、差は１
ａ＝２のとき、差は４
ａ＝３のとき、差は９
ａずつ離れた自然数のとき、差はａ²

②
真ん中のＢをｎとする。
ａずつ離れるので、Ａ＝ｎ－ａ、Ｃ＝ｎ＋ａ
イ…ｎ－ａ、ウ…ｎ＋ａ

エ
ｎ²－（ｎ－ａ）（ｎ＋ａ）
＝ｎ²－（ｎ²－ａ²）
＝ａ²

大問４（関数）

（１）①
ｙ＝ｘ²にｘ＝－２を代入。
ｙ＝（－２）²＝４

②
Ａ（－２、４）→Ｂ（１、１）
右に３、下に３。
ＡＢを斜辺とする直角三角形をつくると、等辺３の直角二等辺。
１：１：√２より、ＡＢ＝３√２

③
ＯＢは傾き１。
Ａから右に２、上に２移動して、切片は４＋２＝６
ｙ＝ｘ＋６

（２）
ｙ＝ｘ²に最大値ｙ＝９を代入→ｘ＝±３
ｘ≧－１だから、ｘ＝３
ｘの変域は原点を通過するので、ｘ＝のとき最小値ｙ＝０
ア…３、イ…０

（３）①

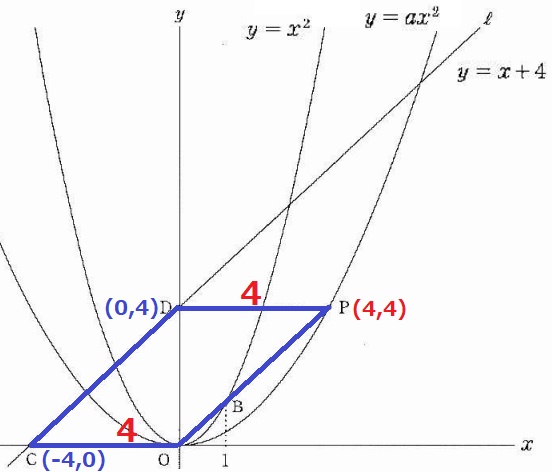
ｙ＝ｘ＋４から、Ｃ（－４、０）Ｄ（０、４）
平行四辺形の対辺は等しい→ＣＯ＝ＤＰ＝４なのでＰのｘ座標は４。
ｙ座標はＤと同じ４。
ｙ＝ａｘ²にＰ（４、４）を代入。
４＝16ａ
ａ＝１/４

②

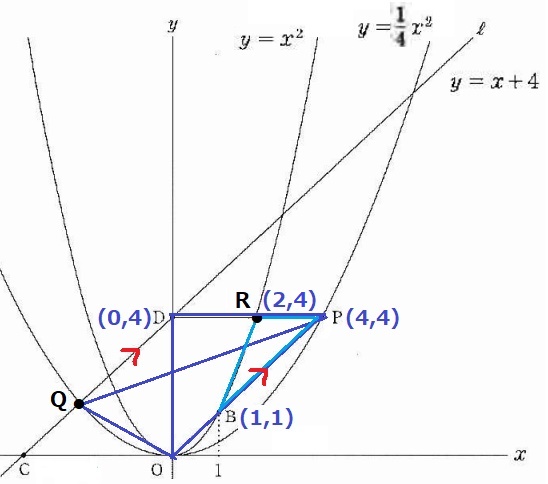
ＯＰとＱＤは傾き１で平行。
△ＯＰＱを△ＯＰＤに等積変形する。

Ｒ座標を求める。ｙ＝ｘ²にｙ＝４を代入。
Ｒのｘ座標はｘ＞０だから、Ｒ（２、４）

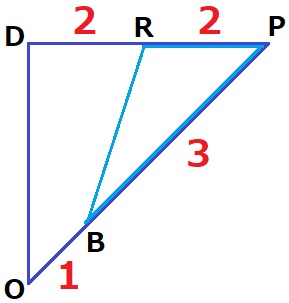
隣辺比から面積比を求める。
△ＯＰＤ（△ＯＰＱ）：△ＢＰＲ
＝ＯＰ×ＤＰ：ＢＰ×ＲＰ
＝４×４：３×２
＝８：３

大問５（平面図形）

（１）
△ＯＰＱも直角二等辺。
∠ＯＰＱ＝45°

（２）①

Ｑを通る直線ℓの垂線の作図。

②
△ＰＣＯ≡△ＯＤＱの証明。

仮定より、ＯＰ＝ＱＯ、∠ＰＣＯ＝∠ＯＤＰ＝90°
△ＰＣＯの内角より、∠ＯＰＣ＝180－90－∠ＣＯＰ＝90－∠ＣＯＰ（×）
また、∠ＱＯＤ＝180－90－∠ＣＯＰ＝90－∠ＣＯＰ（×）
よって、∠ＯＰＣ＝∠ＱＯＤ（●）
斜辺と１つの鋭角が等しいので合同。

（３）①

回転移動で、ＡＯ＝ＰＯ＝２
△ＡＯＲは直角二等辺、辺の比は１：１：√２→ＲＯ＝√２
ＰＲ＝ＰＯ－ＲＯ＝２－√２

②

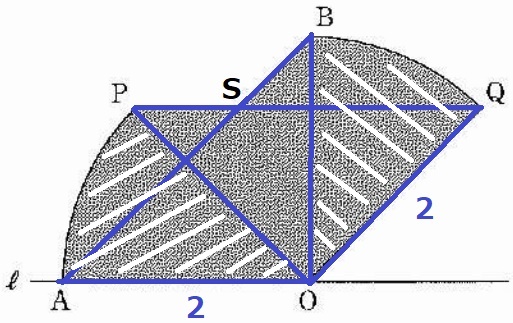
２つの直角二等辺を描く。
弧ＡＰと弧ＢＱから２つの扇形を先に求める。
それぞれ中心角は45°、足して90°だから、
２×２×π×１/４＝π
残りの四角形ＯＢＳＰをどう求積するか。

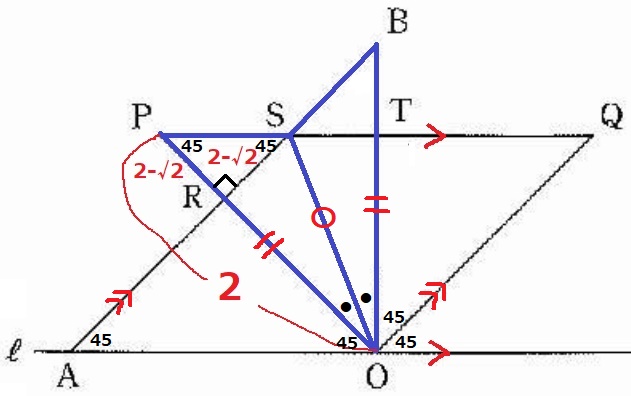
前問でＰＲの長さを求めたので、これを１辺とする△ＰＲＳに着目する。
△ＰＲＳは直角二等辺→ＰＲ＝ＳＲ＝２－√２

ＳＯに補助線。
ＳＯを対称の軸とすると、△ＳＯＰと△ＳＯＢは線対称である。
（ＰＯ＝ＢＯ、45°の同位角からＡＳ//ＯＱで２組の対辺が平行。
→平行四辺形ＡＯＱＳの対角線ＯＳは∠ＡＯＱの二等分線、サイドの45°を消すと●が等角）
ＳＲ⊥ＰＯより、△ＳＯＰの底辺をＰＯとすると高さはＳＲである。
四角形ＯＢＳＰ＝△ＳＯＰ×２＝２（２－√２）÷２×２＝４－２√２
求積すべき図形の面積は、π＋（４－２√２）＋１＝π＋４－２√２