2019年度　都立高校入試問題過去問【数学】解説

平均62.3点

問題ＰＤＦ

大問１（小問集合）－79.9％

（１）　95.4％
５＋１/２×（－８）
＝５－４＝１

（２）　93.5％
４（ａ－ｂ）－（ａ－９ｂ）
＝４ａ－４ｂ－ａ＋９ｂ
＝３ａ＋５ｂ

（３）　85.7％
（√７－１）²
＝７－２√８＋１＝８－２√８

（４）　88.3％
４ｘ＋６＝５（ｘ＋３）
４ｘ＋６＝５ｘ＋１５
ｘ＝－９

（５）　92.1％
連立方程式。
うしろの式を２倍して加減してもいいし、代入法でもOK。
ｘ＝４、ｙ＝６

（６）　69.0％
解の公式を適用。
ｘ＝[－１±√{１²－４・１・（－９）}]/（２・１）
＝（－１±√３７）/２

（７）　39.2％
全体…₅Ｃ₃＝１０通り
積が３の倍数→３のカードは必ずとる。
残り２枚は何でもいい。
４枚から２枚を選ぶ組合せ…₄Ｃ₂＝６通り
したがって、６/１０＝３/５
逆に、取らない２枚の組合せで攻めても、
３を除いた４枚のカードから２枚を選ぶので同じ式になる。
３の倍数が３しかないのでやりやすい。
*誤答では、１/２が多かった。

（８）　74.1％

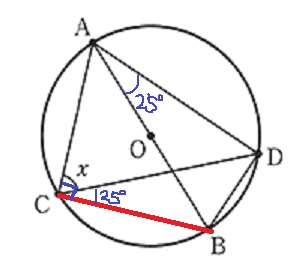
ＢＣに補助線。円周角定理で25°を移動。
半円の弧に対する円周角は90°。
∠ＡＣＤ＝９０－２５＝６５°

（９）　82.2％
作図の基本問題。
Ａを通る垂線を描いて、ＡＢの長さを垂線に持ってくる。
交点がＣ。

大問２（式の証明）－29.0％

（１）　52.8％
正方形を並べ、周りの長さを式で求める。

定石としては、最初が２ａ、後ろが２ａ。
間のくの字は２つ合わせてａで、その数は間の数だからｎ－１個。
これが左右に２つある。
Ｌ＝２ａ＋２ａ＋ａ×（ｎ－１）×２
＝４ａ＋２ａ（ｎ－１）
＝２ａ＋２ａｎ＝２ａ（ｎ＋１）→エ

代数的に考えて…
ｎ＝２のとき、６ａ＝２ａ×３＝２ａ×（２＋１）
ｎ＝３のとき、８ａ＝２ａ×４＝２ａ×（３＋１）
ｎ＝４のとき、10ａ＝２ａ×５＝２ａ×（４＋１）…
Ｌ＝２ａ×（ｎ＋１）＝２ａ（ｎ＋１）

正方形全体の長さから点線を引いてもＯＫ。

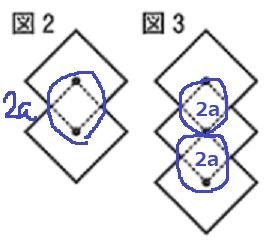
正方形がダブるところ（小さな正方形）の周囲は２ａで、数はｎ－１個。
大きい正方形の周りは４ａなので、
Ｌ＝４ａ×ｎ－２ａ×（ｎ－１）＝２ａｎ＋２ａ＝２ａ（ｎ＋１）
どれも値は同じですね(p_-)

（２）　5.2％!!（部分正答を含む。無答が71.6％！）
円に代わる。解き方の要綱は前問と同じ。

円がきたら中心点から半径の作図！
１個目と２個目の半径から正三角形が表れる。
はじめの角度は240°
最初と最後の円の太線は、２πｒ×240/360×２

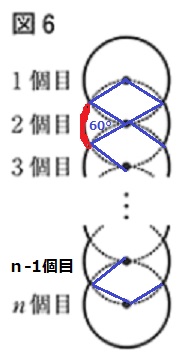
間の弧の中心角は正三角形より60°
注意すべきは、弧の数はｎ－２個であること。
上の赤い弧に注目。
３個目の円までで弧は片側に１個しかないですよね。
先ほどのようにｎ－１個にしない。
太線は、２πｒ×60/360×（ｎ－２）×２
２つを合体。
Ｍ＝２πｒ×240/360×２＋２πｒ×60/360×（ｎ－２）×２
＝１/３×２πｒ×（ｎ＋２）
ℓ＝２πｒだから、該当箇所をℓに変換。
Ｍ＝１/３ℓ（ｎ＋２）
＠＠＠
ちなみに、青山学院でも同じ形が出てました。（７）です。

大問３（関数）－55.2％

（１）　87.5％
ｙ＝－ｘ＋９の式にｘ＝－４を代入。
ｙ＝－（－４）＋９＝４＋９＝１３

（２）①　65.7％
Ｑを作図して直線ｍを作成。

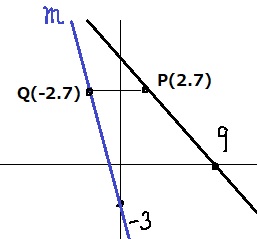
直線ｍの傾きは、右に２、下に１０→－10/2＝－５
切片は－３だから、ｙ＝－５ｘ－３　→ア

②　12.4％！（無答41.7％）
Ｐの座標を（ｓ、－ｓ＋９）とおく。

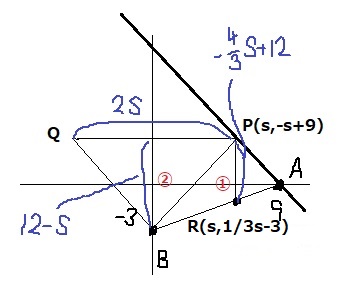
Ｐの真下、ＢＡとの交点をＲとする。
ＢＡは右に９、上に３で傾き１/３。
切片は－３なので、ＢＡ：ｙ＝１/３ｘ－３
Ｒのｘ座標はｓなので、ｙ座標は１/３ｓ－３。
ＰＲ間は－ｓ＋９－（１/３ｓ－３）＝－４/３ｓ＋１２
ここさえ乗り越えれば、あとはいけるかと。
２ｓ×（１２－ｓ）×１/２＝（－４/３ｓ＋１２）×９×１/２×２
－２ｓ²＋２４ｓ＝－２４ｓ＋２１６
２ｓ²－４８ｓ＋２１６
＝ｓ²－２４ｓ＋１０８
＝（ｓ－６）（ｓ－１８）＝０
ｓ＜９なので、ｓ＝６
Ｐのｘ座標は６。

大問４（平面図形）－42.6％

（１）　68.3％

平行四辺形の対角は等しい。
あとは外角定理で、∠ＡＰＣ＝ａ＋５０　→イ

（２）①　57.5％

平行線を活用して錯角。２角で∽。

②　1.9％!!（無答41.3％）
問題集でよく見かける形であり、解法アプローチは複数ある。

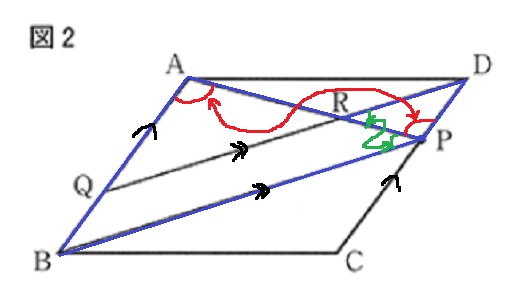
１：２がいっぱいある。

四角形ＱＢＰＤが平行四辺形でＢＰ＝ＱＤ
ＱＲ：ＲＤ＝□２：□１、ＢＰ＝□３

ＲＤ＝□１を△ＲＣＤ∽△ＳＣＰで用いる。
ＳＰ＝□１×２/３＝□２/３
ＢＳ＝□３－□２/３＝□７/３

△ＡＱＲの面積比を２×２＝④とおく。
四角形ＱＢＰＲ＝△ＡＢＰ－△ＡＱＲ＝③×③－④＝➄
四角形ＱＢＰＲは台形なので、面積➄を上底＋下底の和（□５）から案分する。
四角形ＱＢＰＲ＝➄×（□２＋□7/3）/□５＝➄×13/15＝〇13/3
△ＡＱＲ：四角形ＱＢＳＲ＝４：13/3＝１２：１３

＠別解＠
四角形ＱＢＳＲが変な形をしているので、
これをスッキリさせるため、延長して外側に三角形を作るのも手。

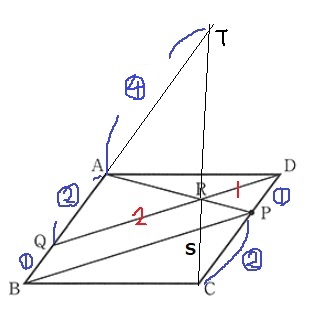
ＢＡとＣＲの延長線の交点をＴとする。
△ＴＱＲ∽△ＣＤＲから、ＴＱ：ＣＤ＝ＱＲ：ＤＲ＝２：１
ＴＱ＝③×２＝⑥
ＴＡ＝⑥－②＝④

△ＡＱＲは、△ＴＱＲの面積をＴＡ：ＡＱ＝④：②で分ける。
(⑥×⑥)×②/⑥＝⑫
四角形ＱＢＳＲ＝△ＴＢＳ－△ＴＱＲ
＝⑦×⑦－⑥×⑥＝⑬
したがって、△ＡＱＲ：四角形ＱＢＳＲ＝１２：１３

＠雑記＠

ＱＣに補助線を引いてネチネチやってたら全部でました。
真ん中が④（＝10/3＋2/3）の平行四辺形で、図形全体が点対称です。

大問５（空間図形）－35.3％

（１）　57.6％
ここも取りたいところ。

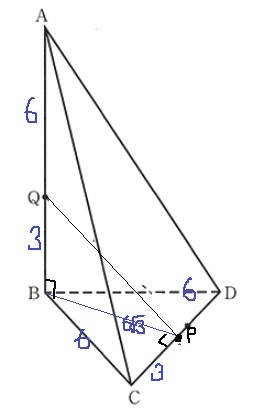
三平方でもいいが、よくみると△ＢＣＰと△ＰＱＢは合同。
ＢＣ＝ＰＱ＝６ｃｍ

（２）　12.6％！（無答35.5％）
最後のわりには素直な設問。
底面を△ＡＱＣで捉える。

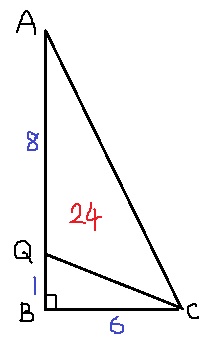
底面積は２４ｃｍ²

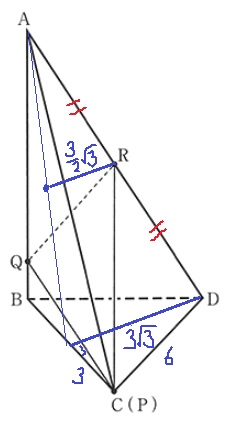
正三角形ＤＢＣの高さ＝３√３をもとに、
求める立体の高さは３√３/２ｃｍとなる。
２４×３√３/２×１/３＝１２√３ｃｍ³

2019年度（都立）
社会…平均52.7点　理科…平均67.1点　英語…平均54.4点
その他は下記リンクの目次からどうぞです。
公立高校入試解説ページに戻る