2022年度　岡山県公立高校入試問題過去問【数学】解説

平均59.7点
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

①　95.0％（部分正答0.5％）
２－（－４）
＝２＋４
＝６

②　95.0％
（－56）÷７－３
＝－８－３
＝－11

③　93.0％
２（３ａ－ｂ）－（ａ－５ｂ）
＝６ａ－２ｂ－ａ＋５ｂ
＝５ａ＋３ｂ

④　94.5％
14ａｂ×ｂ/２
＝７ａｂ²

⑤　86.0％
（１＋√３）²
＝４＋２√３

⑥　72.5％（部分正答1.0％）
ａｘ²－16ａ
＝ａ（ｘ²－16）
＝ａ（ｘ＋４）（ｘ－４）

⑦　65.5％（部分正答0.5％）
４×４×π×150/360＝20/３πｃｍ²

⑧　63.5％
（ｘ、ｙ）＝（１、－２）を代入して、等式が成り立つものを選ぶ。
ア：３×１－（－２）－１＝４×
イ：３×１＋２×（－２）＋１＝０〇
ウ：３×（－２）＋６＝０〇
エ：１＋１＝２×
イ・ウ

⑨　54.0％

ア：四分位範囲＝第３四分位数（Q3）－第１四分位数（Q1）
箱の長さで、B組の方が大きい。〇
イ：最大値はＡ組が大きい。×
ウ：Ａ組のＱ3はＢ組のＱ2より小さい。×
エ：目盛りが見当たらないが、Ａ組のＱ3が11点くらい→12点以上は25％未満。
Ｂ組のＱ2が12点くらい→12点以上は50％以上で２倍以上。〇
ア・エ

⑩　39.5％（部分正答4.0％）

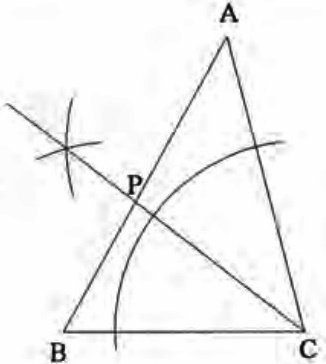
『点Ｐと直線ＡＣ、ＢＣとの距離は等しい』
→∠ＡＣＢの二等分線。
これと辺ＡＢとの交点がＰ。

大問２（方程式）

①　44.5％（部分正答2.5％）
ペットボトルのポイントは20ａ。
新聞紙のポイントは７ｂ。
この和が500ポイント以上だから、
20ａ＋７ｂ≧500

②（１）　91.5％（部分正答3.0％）
重さで等式。　ｘ＋ｙ＝39…①
ポイントで等式。　45ｘ＋10ｙ＝1160…②

（２）　82.0％（部分正答2.0％）
先の方程式を解く。
②－①×10をすると、ｘ＝22
①に代入して、ｙ＝17
アルミ缶…22ｋｇ、スチール缶…17ｋｇ

大問３（関数）

①（１）　84.5％（部分正答0.5％）
ｙ＝ａｘ²にＡ（２、２）を代入。
２＝４ａ
ａ＝１/２

（２）　84.0％（部分正答1.5％）
ｙ＝－ｘ²にｘ＝２を放り込んで、
ｙ＝－２²＝－４

（３）　19.5％！（部分正答5.5％）

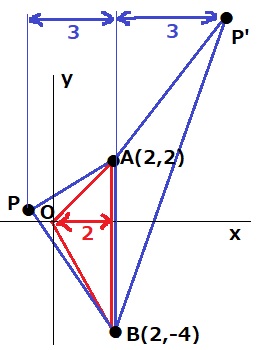
△ＯＡＢと△ＰＡＢは底辺ＡＢが共通する。
面積比が２：３⇒高さが２：３になればいい。
ＯとＡ（Ｂ）のｘ座標の差が２なので、ｘ＝２から３離れる。
２－３＝－１、２＋３＝５
ｘ＝－１、５

②（１）　61.0％（部分正答3.0％）
各座標をｔで表す。

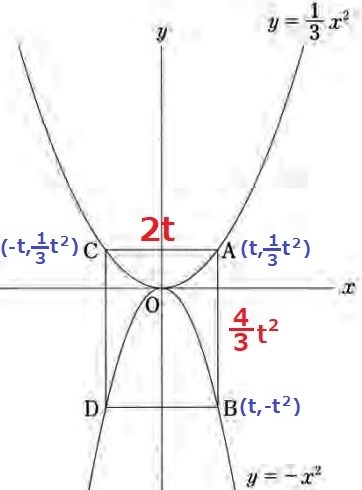
Ａ（ｔ、１/３ｔ²）Ｃ（－ｔ、１/３ｔ²）
ＡＣ＝ｔ－（－ｔ）＝２ｔ

（２）　17.0％！（部分正答0.5％）
Ｂ（ｔ、－ｔ²）
ＡＢ＝１/３ｔ²－（－ｔ²）＝４/３ｔ²

長方形ＡＢＣＤの半周の長さは６。
４/３ｔ²＋２ｔ＝６　←３倍
４ｔ²＋６ｔ－18＝０　←÷２
２ｔ²＋３ｔ－９＝０
解の公式を適用すると、
ｔ＝（－３±√81）/４
＝（－３±９）/４
＝－３、３/２
Ａのｘ座標は正（ｔ＞０）だから、ｔ＝３/２
Ａのｘ座標は３/２。
ｙ＝１/３ｘ²にｘ＝３/２を代入して、ｙ＝３/４
Ａ（３/２、３/４）

大問４（確率）

①（１）　93.5％
Ａ：６＋４＝10→和は８以上〇
Ｂ：６－４＝２→差は２〇
Ｃ：偶数×偶数＝偶数→積は奇数ではない×
２個

（２）　56.0％（部分正答0.5％）
全体は６×６＝36通り
差が２になる組み合わせは、（６、４）（５、３）（４、２）（３、１）とこれらの逆。
計８通り。
確率は８/36＝２/９

②　44.0％（部分正答35.0％）
説明問題だが、ＡとＣの確率を書いて比較すれば足りる。
和が８以上の組み合わせは、（２、６）（３、５～６）（４、４～６）（５、５～６）（６、６）
数字が異なるペアの逆を含めると計15通り。
Ａの確率は、15/36＝５/12

積が奇数となる組み合わせは〔奇数×奇数〕のみ。
奇数は１・３・５→３×３＝９通り
Ｃの確率は、９/36＝１/４
５/12＞１/４だから、Ａの方が起こりやすい。

③　52.0％
答案では式も記入する。
Ｂの確率が２/９だったので、全体の1800回にこれをかける。
1800×２/９＝400回

④　57.0％
Ａ～Ｃはアメ１個ずつなので、Ｂは400個。
前問と同じようにＡとＣを算出する。
Ａ：1800×５/12＝750個
Ｃ：1800×１/４＝450個
したがって、750＋400＋450＝1600個
ウ

大問５（空間図形）

①　68.0％

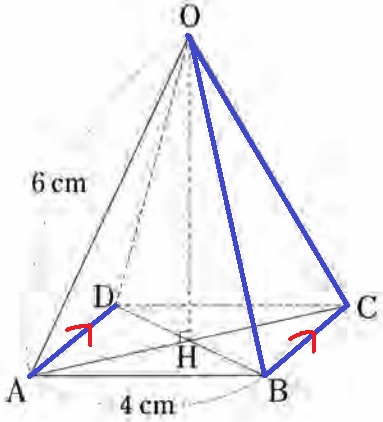
ウ：ＡＤ//ＢＣで、ＢＣは面ＯＢＣ上の直線だからＡＤ//面ＯＢＣ
直線ＡＤと面ＯＢＣをそれぞれ延長しても両者は交わらない。

ア：ＯＡとＢＣはネジレ。
イ：ＯＢとＯＤには”Ｏ”が含まれるのでＯで交わる。ネジレではない。
エ：面ＯＡＢと底面積である面ＡＢＣＤは垂直ではない。

②　55.5％（部分正答0.5％）
△ＡＢＣは直角二等辺。
辺の比は１：１：√２なので、ＡＣ＝４√２ｃｍ
ＨはＡＣの中点だから、ＡＨ＝４√２÷２＝２√２ｃｍ

③　47.0％（部分正答1.0％）
△ＯＡＨで三平方→２√７ｃｍ
正四角錘の体積は、４×４×２√７÷３＝32√７/３ｃｍ³

④（１）あ…45.0％、い…60.5％、う…38.0％、え…9.5％!!（部分正答28.5％）

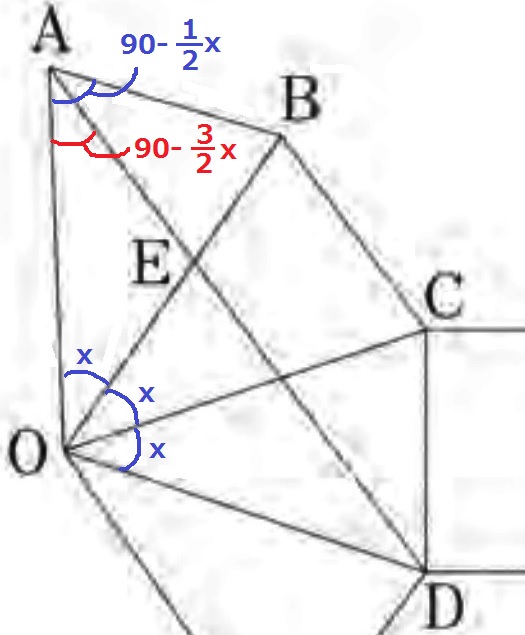
△ＯＡＢは二等辺三角形。
∠ＯＡＢ＝（180－ｘ）÷２＝90－１/２ｘ

△ＯＡＤも二等辺三角形。
正四角錐Ｏ—ＡＢＣＤから△ＯＡＢ≡△ＯＢＣ≡△ＯＣＤで、
∠ＡＯＢ＝∠ＢＯＣ＝∠ＣＯＤ＝ｘ
∠ＡＯＤ＝３ｘ
∠ＯＡＤ＝（180－３ｘ）÷２＝90－３/２ｘ
あ…オ、い…イ、う…カ

え
前問の角度を使う。
∠ＥＡＢ＝∠ＯＡＢ－∠ＯＡＤ
＝（90－１/２ｘ）－（90－３/２ｘ）
＝ｘ
∠ＡＯＢ＝∠ＥＡＢ
共通角で、∠ＯＢＡ＝∠ＡＢＥ
２角が等しいので、△ＯＡＢ∽△ＡＥＢ

（２）　1.5％!!

△ＯＡＢ∽△ＡＥＢから、△ＡＥＢも二等辺三角形。
ＡＥ＝ＡＢ＝４ｃｍ
ＡＤとＯＣの交点をＦとする。
図形全体が左右対称で、ＤＦ＝ＡＥ＝４ｃｍ

真ん中のＥＦをどうするか？
等角に印をつけていくと、対頂角で∠ＡＥＢ＝∠ＯＥＦ
共通角の∠ＥＯＦ＝∠ＢＯＣとあわせると、２角相等で△ＯＥＦ∽△ＯＢＣ
また、△ＯＡＢ∽△ＡＥＢ→ＯＡ：ＡＢ＝ＡＥ：ＥＢから、ＥＢ＝４×４/６＝８/３ｃｍ

ＯＥ＝６－８/３＝10/３ｃｍ
ＯＥ：ＥＢ＝10/３：８/３＝⑤：④
△ＯＥＦ∽△ＯＢＣの相似比は⑤：⑨
ＥＦ＝４×⑤/⑨＝20/９ｃｍ
ＡＤ＝４＋４＋20/９＝92/９ｃｍ