平均26.8点(前年比;-0.6点)
問題はこちら→リセマムさん(追加問題)
大問1(小問集合)
(1)ア
-6+9
=3
イ
-15×3/10
=-9/2
ウ
√75-4√3
=5√3-4√3
=√3
エ
(x+y)/2-(2x-y)/3
={3(x+y)-2(2x-y)}/6
=(3x+3y-4x+2y)/6
=(-x+5y)/6
(2)
x2-x-56
=(x-8)(x+7)
(3)
6a+5b≦1000
以下なので1000円を含む。
(4)
反比例:y=a/x
a=xy=2×4=8
y=8/x
(5)
x2-7x+2=0
因数分解ができないので、解の公式を適用。
x=(7±√41)/2
(6)
円周角定理の逆。
『2点○、○が直線○○について同じ側にあって、∠○○○=∠○○○が成り立つとき、
4点○、○、○、○は同じ円周上にある』
ざっくり言うと、ある直線と同じ側にあって、2角が等しいと同じ円周にある。

①・④
(7)
円錐の表面積。
母線は3:4:5から5cm。
側面積の扇形の中心角は、[×半径/母線]で処理しよう。
3×3×π+5×5×π×3/5
=24πcm2
大問2(方程式)
(1)ア
Bがx人、Cがy人
Aは5人なので、x+y+5=33…①
後半の文から、もう1つを立式。
『Aと等しくなった』ので、計算結果は5
2x-y=5…②
イ
前問の連立を解くと、x=11、y=17
Bは11人、Cは17人
(2)ア
10以下の素数を述べる。
2・3・5・7
*1は素数に含まない!
イ
素数を選択する。
23・37・71
*91=7×13
@倍数のルール@
2の倍数…偶数、3と9の倍数…位の和が3・9の倍数
4の倍数…下2桁が4の倍数 8の倍数…下3桁が8の倍数
5の倍数…1の位が0か5 6の倍数…偶数であり、かつ位の和が3の倍数
*7だけは自力でやった方が早い。
ウ
答案では過程も記述する。
x2+52=17x
x2-17x+52
=(x-4)(x-13)=0
xは素数なので、x=13となる。
大問3(確率・規則)
(1)a
3枚のコインを投げる。
23=8通り
b
和が4以上となるには、4のコインは必ず表。
残り2枚では和が4以上にならないので、残り2枚は表・裏どちらでもいい。
2枚のコインの表裏の出方→22=4通り
4/8=1/2
(2)a
2のコインが1枚追加される。
すべての出方は24=16通り
和が4になるパターンは、【4だけ表、残り3枚が裏】
もしくは、【2枚の2が表、残り2枚が裏】の2パターン。
2/16=1/8
b
和が4以上になるパターンを数える。
4のコインの表裏で場合分け。
【4が表である場合】
残り3枚は何でもよい。
23=8通り
【4が裏である場合】
2のコイン2枚は必ず表。
1のコインは何でも良い→2通り
計10通り
10/16=5/8
*前問の答え(和が4の結果)から、和が5以上となる場合を足してもいい。
逆に和が4未満となる結果を出して、全体から引いてもいい。
(2)ア
☆は2の倍数、○は3の倍数で青。
最小公倍数の6回ごとに、☆と○は共に青になる。
6回
イ
☆と○は6の倍数
♡は4の倍数か、4の倍数-1
6の倍数と4の倍数の偶数。4の倍数-1は奇数。
→4の倍数-1回では、☆と○は青ではない。
初めて3つが青になるのは、6と4の最小公倍数である12回。
ウ
方針としては全てが青でない回数を直接調べるか、
もしくは1つでも青となる回数を調べて100から引くか。
ここでは、○と☆が1つでも青となる回数を計算してから、
○と☆がともに赤となる回数を導き、そのなかで♡も赤である回数を調べる。
☆は2の倍数で青となる→50回
○は3の倍数で青となる→33回
☆と○が両方つくのは6の倍数→100÷6=16…4→16回
☆と○が1つでも青となるのは、50+33-16=67回
☆と○が赤になるのは、100-67=33回
ここから♡を考える。
この67回は2の倍数でなく、かつ3の倍数でない数の個数である。
4の倍数であれば必ず2の倍数なので、67回に含まれない。
そこで、4の倍数-1に狙いを定める。
100未満で最大の4の倍数は96なので、最後は95となる。
【3・7・11・15・17・23・27・31・35…95】
この数列の個数を求める。公差は4
(95-3)÷4+1=24回
この数列には○の3の倍数が含まれるので、
重複を避けるために3の倍数を抜きたい。
【3・7・11・15・17・23・27・31・35…87・91・95】
3から始まり、3個おきに3の倍数が表れ、最後は87
【(3・7・11)・(15・17・23)・(27・31・35)…(87・91・95)】
↑こう区切ると、3の倍数を除いた4の倍数-1の個数が見えてくるはず。
つまり、全体の2/3倍。
24×2/3=16回
33回-16回=17回

ベン図で整理するとこんな感じ。
4の倍数は2の倍数の部分集合。
4の倍数が偶数なので、4の倍数-1は奇数。
4の倍数-1と2の倍数&4の倍数の集合は交わらない。
大問4(関数)
(1)ア
18=32a
a=2
イ
y=ax2
x=1のとき、y=a
x=3のとき、y=9a
(9a-a)/(3-1)=-2
8a=-4
a=-1/2
@別解@
y=ax2においてp→qの変化の割合はa(p+q)
a(1+3)=-2
4a=-2
a=-1/2
(2)ア
A(-1、2)→B(2、8)
右に3、上に6だから、傾きは2
Aから右に1、上に2いくと、切片は4
y=2x+4
イ
C(0、4)
Dはx軸を対称の軸としてCを対称移動した点だから、
D(0、-4)
ウ
お馴染みの等積変形。
底辺はAB間のx座標、高さはCD間のy座標。
△ABD=3×8÷2=12
エ

等積変形で1個目。
ABの傾きが2なので、平行線の傾きも2
△OPDでOD:OP=2:1となるので、OP=2
P(2、0)
もう1つが難所・・。
AとBは位置が決まっているのでx軸上へ動かせない。
Pを反対側に動かすことを考える。

AB:y=2x+4とx軸との交点をEとおく。
0=2x+4
x=-2
E(-2、0)
EPの距離は4。これをx軸上で負の方向に4進んだP’(-6、0)が答え。
-6、2
大問5(図形)
(1)
ネジレの位置→(延長しても)交わらないor平行でない。
①DN→平行 ②GH→ネジレ ③EF→延長して交わる ④FG→ネジレ
②・④
(2)
1辺が3cmの正方形の対角線。
EG=3√2cm
(3)ア
立体図形のなかで相似の証明。
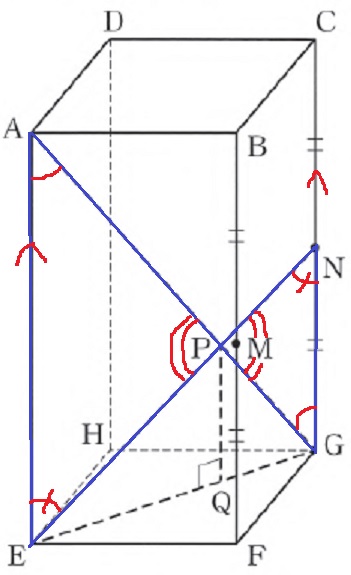
AE//CGから錯角。
または対頂角を加えて2角が等しい点を指摘する。
イ
前問の△APE∽△GPNを用いる。
EP:NP=AE:GN=6:3=2:1
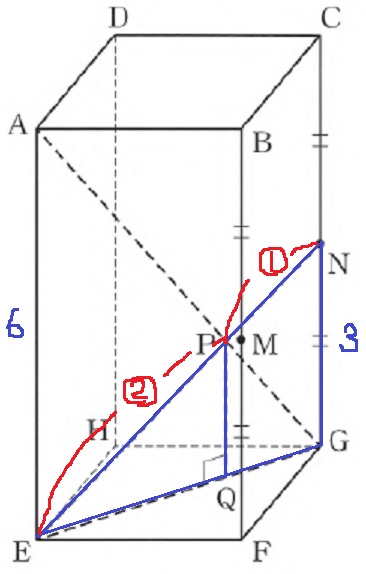
ここから、△EPQ∽△ENGに視点を変える。
PQ:NG=EP:EN=2:3
PQ=3×2/3=2cm
ウ
回転体の半径はEQ
(2)でEG=3√2と求めており、前問の△EPO∽△ENGから、
EQ:QG=2:1→EQ=3√2×2/3=2√2cm

下手な図で申し訳ない(-_-;)
下が円柱、上が円錐となる。
2√2×2√2×π×2+2√2×2√2×π×4×1/3
=80/3πcm3
追加問題1(格子点)
(1)
OQに補助線をひく。
△OPQで三平方。
PQ=√(82-12)=3√7
(2)
問題点は3√7が7以上か7未満かの判定。
3√7ではなく、√63で考えよう。
√49(7)<√63<√64(8)なので、3√7は7以上。
格子点となる座標のy座標は、0・1・2・3・4・5・6・7の8個。
@√7の近似値@
√7=2.6457…
*参考*
√2=1.41421356…(一夜一夜に人見ごろ)
√3=1.7320508…(人並みにおごれや)
√5=2.2360679…(富士山麓オウム鳴く)
(3)
上と同様に直角三角形を作成して高さを判定する。
x=2のとき、
√(82-22)=√60
√49<√60<√64なので、7<√60<8
→格子点は8個
x=3のとき、√(82-32)=√55
7<√55<8→8個
x=4のとき、√(82-42)=√48
6<√48<7→7個
x=5のとき、6<√39<7→7個
x=6のとき、5<√28<6→6個
x=7のとき、3<√15<4→4個
x=8のとき、(0、8)のみ→1個
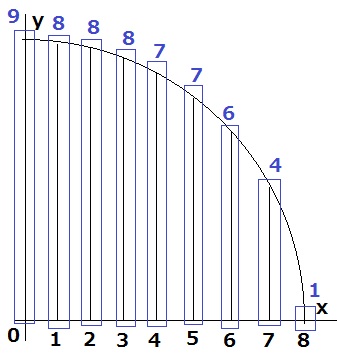
これらを合計すると58個
@もっと効率の良い方法はないのか!?@
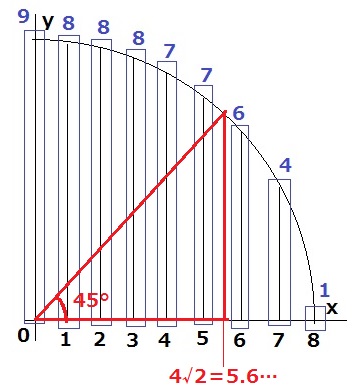
45度線をひき、扇形OABを半分に分ける。
1:1:√2より、x座標は8×1/√2=4√2
√2=1.4142…だから、4√2=4×1.4=5.6…
5と6の間にくる。
赤い直角三角形の内部と周上の格子点は、
1+2+3+4+5+6=21個
x=6とx=7は先ほどの手法で地道に調べる。
扇形OABの半分の格子点は、
21+6+4+1=32個
これを2倍して、重複する45度線上の格子点をひけばいい。
重複する45度線上の格子点は6個(x座標0~5)
32×2-6=58個
(4)
(3)さえ乗り越えられれば取りやすい。
まずは格子点を確認。
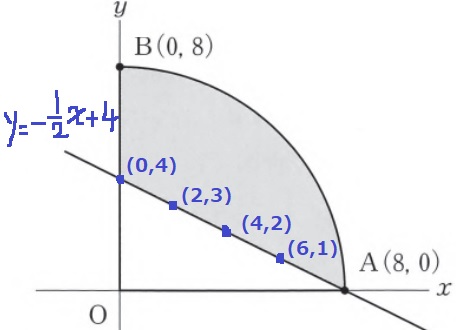
扇形OABから下の部分を取り除けばいい。
どう数えるかは自由。

サボは横方向で数えました。
y=3のとき、(0、3)(1、3)
y=2のとき、(0、2)(1、2)(2、2)(3、2)…
気を付けるべき点は、y=-1/2x+4上の格子点は残しておくこと!
合計は、2+4+6+8=20個
58-20=38個
*ちなみに、本問のグラフはx2+y2=82
円の方程式といい、高校数学で習います。
追加問題2(投影)
(1)ア
正方形A’B’C’D’の1辺を知りたい。
PQ:QR=12:60=1:5
△PQC∽△PRC’から、PC:CC’=1:5
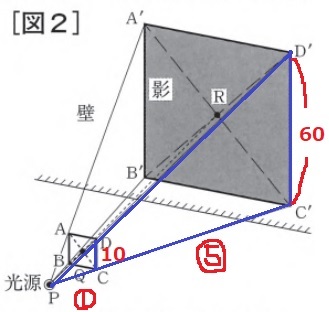
△PDC∽△PD’C’に視点を変える。
D’C’=10×6/1 =60cm
正方形A’B’C’D’=60×60=3600cm2
イ
図形の位置を変えたとき、投影がどう変化するか。
〔図4〕から考える。
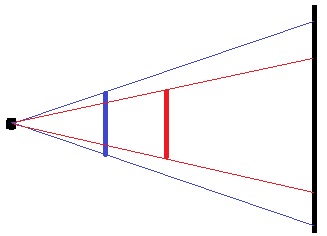
青は光源から近い。赤は遠い(青と赤は同じ長さです)
図形を遠ざけると、投影された図形の面積は減少する。
(*図形が光源から近いと影は大きい、光源から遠いと影は小さくなる)
〔図3〕では正方形の下の辺BCを軸に、上の辺ADを奥に倒す。
光源からの距離はBCが近く、ADが遠い。
ということは、投影された図形はB’C’が長く、A’D’が短くなるので台形となる。
d
(2)ア
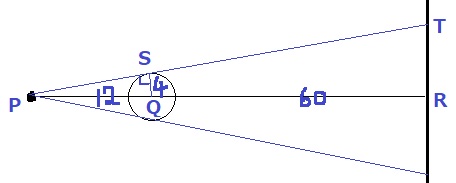
円QはPTとSで接する。半径QSとPTは垂直の関係。
△PQSで三平方→PS=8√2
求める影の半径はTRにあたる。
△PQS∽△PTRより、
QS:TR=PS:PR=8√2:72
TR=4×72/8√2=18√2cm
イ
追加問題は偏差値の高いところだけのようだが、
最後の問題はどれほど正解できたのだろうか(;´Д`)
壁に立方体をくっつけるとき、『影の形を円のまま変化させないようにする』
立方体を大きくし過ぎると、影が円にならなくなる。
立方体が円の影にひっかかりやすいところは四つ角。
全体を真横からみたとき、捉えるべき図形は(2)のように真正面ではなく、
45°傾いた図形となる。

URをxとおく。
URは立方体の1辺であり、UVは正方形の対角線の半分。
1:1:√2の直角三角形から、UV=x×1/√2=√2/2x
△PVUの辺の比から、PU=√2/2x8√2/4=2x
PR=2x+x=3x=72
x=24
立方体の1辺は24cm



コメント