2019年度　高知県公立高校過去問Ａ日程【数学】解説

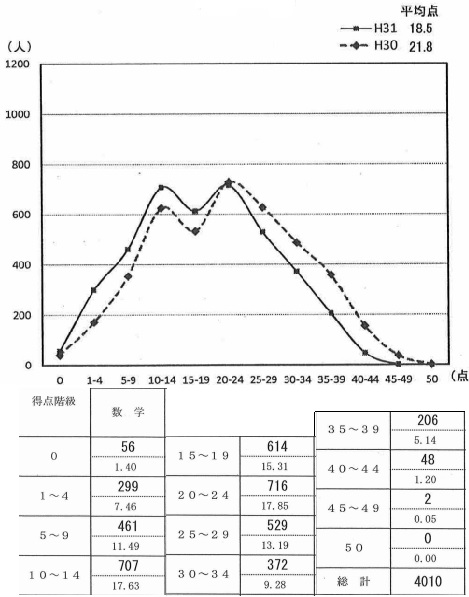
平均18.5点（50点満点）

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）　91.8％
２－９－（－４）
＝２－９＋４＝－３

（２）　64.9％
（７ｘ＋２）/３＋ｘ－３
＝（７ｘ＋２＋３ｘ－９）/３
＝（10ｘ－７）/３
*誤答では、分母を含めて計算しなかった、10ｘ－７が多い。
また、通分せずにそのまま計算している（８ｘ－１）/３もあった。

（３）　73.5％
８ａ÷（－４ａ²ｂ）×（ａｂ²）
＝－２ｂ

（４）　71.0％
４√３÷√２＋√54
＝２√６＋３√６
＝５√６

大問２（小問集合）

（１）　47.8％
ａ×ｂ×１/２＝15
ａｂ/２＝15
ｂ＝30/ａ
*誤答では15/ａ、15ａが多い。

（２）　39.1％（部分点19.0％、無答15.9％）
解答用紙では過程も記述する。
ｘ＝２を代入。
２²－２ａ－12＝0
２ａ＝－８
ａ＝－４

これをもとの式のａに代入。
ｘ²－（－４）ｘ－12
＝ｘ²＋４ｘ－12
＝（ｘ－２）（ｘ＋６）＝０
もう１つの解は、ｘ＝－６
*誤答では、ａに２を代入したり、計算ミスがあった。

（３）　36.1％
９/２＜√ｎ＜５
根号が邪魔なので、すべてを２乗する。
81/４（20・１/４）＜ｎ＜25
自然数ｎは、21・22・23・24→４個

（４）　66.0%
反比例：ｙ＝ａ/ｘ
ａ＝ｘｙ＝－３×８＝－24
ｙ＝－24/６＝－４

（５）　37.2％
ｙ＝ｘ²の傾きは正なので、下に凸のグラフ。
ｙの最小値０は、ｘ＝０のとき（原点）。
ｘ＝２のとき、ｙ＝４なので、
ｙの最大値９がｘ＝ａにあたる。（ａは原点より左、つまり負）
９＝ａ²
ａ＝±３
ａは負なので、ａ＝－３
*誤答は０や３が多かった。

（６）　41.9％
解答では途中式も要求される。
和と差の平方の形に持っていく。
103²－97²
＝（103＋97）（103－97）
＝200×６＝1200

（７）　53.6％
円柱になります。
４×４×π×６＝96πｃｍ³

（８）　67.7％
中央値（メジアン）の意味さえわかれば、サッと選べる。
70人の中央値は35番目と36番目の平均値。
イ

（９）　31.2％！（部分点0.2％、無答12.2％）
作図問題。
①ＢＰ＝ＣＰ→ＢＣの垂直二等分線
②∠ＢＣＰ＝∠ＡＣＰ→∠ＡＣＢの二等分線
この交点が点Ｐとなる。

大問３（数量変化）

（１）　14.3％！
０≦ｘ≦６→ＱがＦに着くまで。
ＢＰ＝ｘ、ＣＱ＝２ｘで、四角形ＰＢＣＱは台形。
（ｘ＋２ｘ）×８÷２＝12ｘｃｍ²
*誤答には、ｘが含まれていない解答が多くみられた。

（２）　9.6％!!
ＰＱが長方形ＢＣＦＥを２等分する。
ＰＢＣＱは台形なので、長方形との面積比は上底＋下底の和で決まる。
長方形の対辺であるＢＥ＋ＣＦ＝24だから、
ＢＰ＋ＣＱ＝12のときに、ＰＱが長方形を２等分する。

はじめは、ＱがＰよりも上にあるとき。
ｘ＋２ｘ＝12
ｘ＝４

２つ目はＱがＦを折り返して、Ｐよりも下にあるとき。
ＣＦ間の往復距離は、12×２＝24
ＣＱ＝24－２ｘ
ｘ＋（24－２ｘ）＝12
ｘ＝12
したがって、ｘ＝４、12

（３）　0.9％!!!
ＱがＦに着くまでの０≦ｘ≦６では、ＤＰ＝ＤＱとはならない。
なぜなら、初期状態がＤＰ（ＤＢ）＞ＤＱ（ＤＣ）で、
Ｑが先にＤに近づくので、ＤＰ＞ＤＱの関係が継続する。
ＤＰ＝ＤＱとなるのは、ＱがＦを折り返した後（６≦ｘ≦12）のとき。

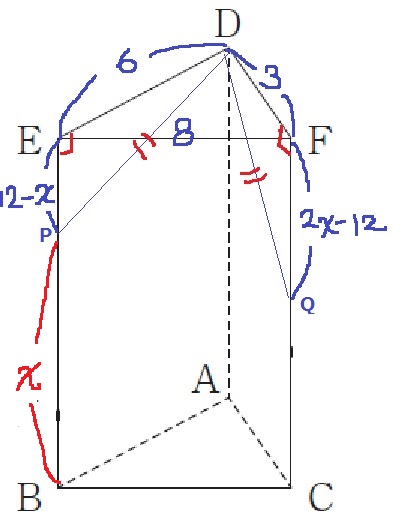
ＥＰ＝12－ｘ、ＦＱ＝２ｘ－12（Ｑが進んだ２ｘから片道12を引く）
△ＤＥＰと△ＤＦＱに着目する。
ＤＰ＝ＤＱと三平方から等式を作成する。
６²＋（12－ｘ）²＝３²＋（２ｘ－12）²
36＋144－24ｘ＋ｘ²＝９＋４ｘ²－48ｘ＋144
３ｘ²－24ｘ－27
＝ｘ²－８ｘ－９
＝（ｘ＋１）（ｘ－９）＝０
ｘ＞０なので、ｘ＝９
ＢＰ＝９

ＦＱ＝２×９－12＝６より、ＱＣ＝６

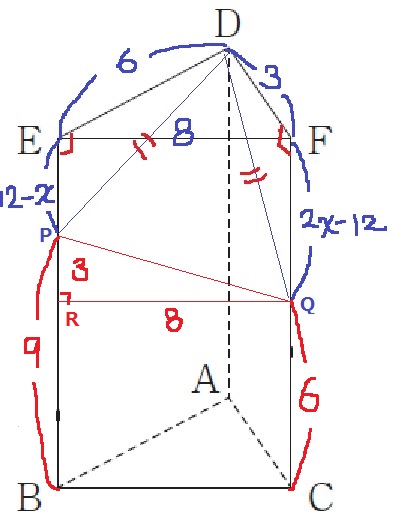
ＱからＰＢに向けて垂線、その交点をＲとする。
△ＰＱＲで三平方。
ＰＱ＝√（８²＋３²）＝√73ｃｍ

大問４（確率）

（１）①　31.6％！
【大】の出目の箱から１個取り出し、【小】の出目の箱に移動させる。
１回だけの操作で空になるには、【大】で１を出し、【小】で２～６を出す。
すると、１の箱が空になる。

２つのサイコロの出目のパターンは、６×６＝36通り
【小】の２～６→５通り。
５/36

②　29.5％！
どうすれば、『玉の数が同じ箱が３つできる』だろうか？
２を真ん中に、３→１に１個わたす。２個が３つできる。
３を真ん中に、４→２に１個わたす。３個が３つできる。
同様に４を真ん中、５を真ん中にして一方から他方に渡す。
計４通り。
４/36＝１/９

（２）　22.5％！
今度は【大】の箱をすべて【小】の箱に移す。
大１のとき、小＝2・３・４・５
大２のとき、小＝１・３・４
大３のとき、小＝１・２
大４のとき、小＝１・２
大５のとき、小＝１
大６のとき、なし。
計12通り。
12/36＝１/３

大問５（関数）

（１）　56.9％
Ａ（２、４）
菱形ＯＡＣＢより、Ｃのｙ座標はＡのそれの２倍。
（０、８）

（２）　10.1％！
『平行四辺形を２等分する直線は必ず対角線の交点（真ん中）を通る』
菱形も長方形も正方形も特別な平行四辺形なので、同様のことが言える。

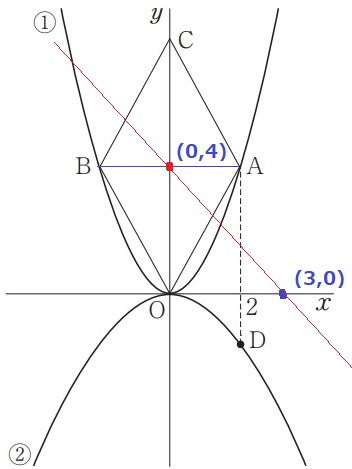
（０、４）→（３、０）
下に４、右に３なので、傾きは－３/４。
切片は４。
ｙ＝－４/３ｘ＋４

（３）　0.5％!!!
手順はつかみやすい方かな？処理過程が煩雑。

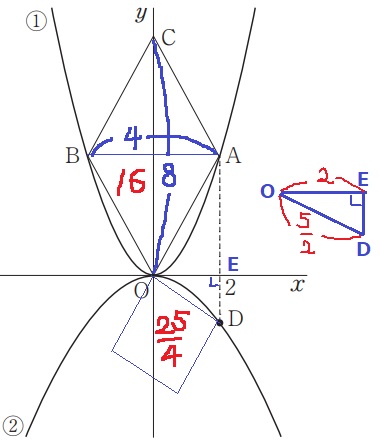
菱形ＯＡＣＢの面積＝４×８÷２＝16
面積比から、正方形の面積＝16×25/64＝25/４
正方形の１辺（ＯＤ）＝√（25/４）＝５/２

（２、０）をＥとする。
△ＯＤＥで三平方→ＥＤ＝３/２
Ｄ（２、－３/２）

これをｙ＝ａｘ²に放り込む。
－３/２＝４ａ
ａ＝－３/８

大問６（平面図形）

（１）　5.9％!!（部分点19.0％、無答26.9％）
△ＡＢＣ∽△ＤＡＦの証明。

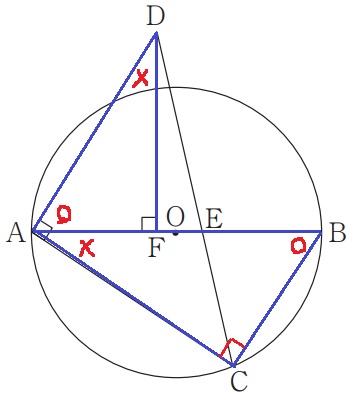
半円の弧に対する円周角から、∠ＡＣＢ＝90°
内角を〇＋×＝90°として調べると、２角が等しい→∽

（２）　0.5％!!!
ＡＤとＣＢが平行っぽい。

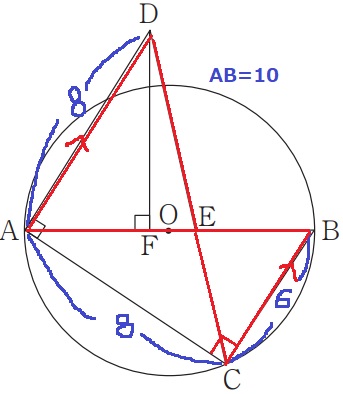
∠ＤＡＣと∠ＡＣＢは同位角の関係にはないが、
ともに90°なので延長線をひいて同位角を作れば、ＡＤ//ＣＢとなる。
錯角や対頂角で、△ＡＥＤ∽△ＢＥＣ
ＡＥ：ＢＥ＝ＡＤ：ＢＣ＝８：６＝４：３
ＡＢ＝10なので、ＡＥ＝10×４/７＝40/７ｃｍ

前問の△ＡＢＣ∽△ＤＡＦを活用する。
△ＡＢＣの辺の比は５：４：３なので、
ＡＦ＝８×３/５＝24/５ｃｍ
よって、ＦＥ＝40/７－24/５
＝32/35ｃｍ
公立高校入試解説ページに戻る