2019年度　慶應義塾湘南藤沢中等部過去問【算数】大問４解説

問題ＰＤＦ
図のように、１～５の数字がかかれたランプが円状にならんでいる。

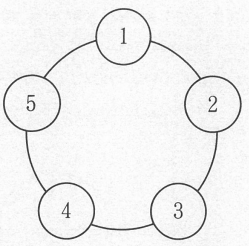
あるランプをおすと、その両どなりの２つのランプが、明かりがついていれば消え、消えていればつく仕組みとなっている。このとき、両どなり以外の３つランプは変わらない。
例えば、①のランプがついていて、③のランプが消えているときに、②のランプをおすと、①のランプが消え、③のランプがつき、②、④、⑤のランプは変わらない。
次の各問いを、最初はすべてのランプがついているものとして答えなさい。
（１）
①→②→②の順番でおしたあと、ついているランプの数は全部で何個になりますか。

（２）
①→④→③→②→⑤→③の順番で押したあと、ついているランプは①～⑤のどれですか。
すべて答えなさい。

（３）
①→③→④→①→⑤→②→③→②→③→④→①→①→②→①→⑤→②→⑤→②→③→□→③の順番でおしたあと、すべてのランプがついていた。
□にあてはまるランプは①～⑤のどれですか。

＠解説＠
（１）
ルールに従って調べる。

試験では消しゴムで〇と×を変えてください。
①・③・④

（２）
同様。６回も押すのでケアレスに注意！
５回目の⑤を押したときに全て点灯する。
①・③・⑤

（３）
21回目の③で全てが点灯したとき、20回目に押したボタンを求める。
さすがに手作業で調べるのは時間がかかるうえにミスが生じやすい。
そこで、前問までの結果からとっかかりをつかむ。

①のボタンが点くか点かないかは、隣のボタンが押された回数による。
つまり、②と⑤が押される回数に依存する。
最初はすべて点いているので、奇数回だと消え、偶数回だと点く。

そこで、□までに各々のボタンが押された回数を数える。
①…５回　②…４回　③…４回　④…２回　⑤…３回
①のボタン→②＋⑤＝７回（奇数回）
②のボタン→①＋③＝９回（奇数回）
③のボタン→②＋④＝６回（偶数回）
④のボタン→③＋⑤＝７回（奇数回）
⑤のボタン→①＋④＝７回（奇数回）
…ということは、□の手前で③のみ点いており、他４つは消えている。

□のうしろは③のボタンを押すので、②と④が点く。
したがって、□で①と⑤を点ければ、すべてが点灯する。
□にあてはまるボタンは④

＠別解＠
偶数回は押してまた押すのだから、押していないのと同じ。
奇数回は１回押すのと同じ。
（１）は①→②→②
②は無視して①を１回だけ押す。
すると、②と⑤が消えるので、①③④が点灯する。
これは、②→①→②でも、①→②→②でも同様の結果になる。

（２）は①→④→③→②→⑤→③
③を無視して、①→④→②→⑤の順で押すと、①・③・⑤が点灯する。
②→①→⑤→④、⑤→②→④→①と押しても①・③・⑤が点灯する。
手順を変えても結果は変わらない！
ボタンを押すと隣のボタンに影響を与える→ボタンを押す回数が重要であって、順番は関係がない。

（３）で押された回数は、
①…５回　②…４回　③…４回　④…２回　⑤…３回
奇数回の①と⑤を１回ずつ押すと、□の手前では③だけが点いているとわかる。
難関中（算数科）解説ページに戻る