2023年度　徳島県公立高校入試問題過去問【数学】解説

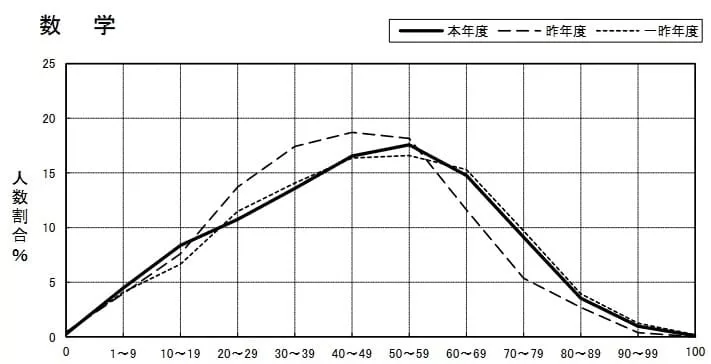
平均46.0点（前年比；＋3.1点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
（－４）×２
＝－８

（２）
５√３－√27
＝５√３－３√３
＝２√３

（３）
ｘ²－14ｘ＋49
＝（ｘ－７）²＝０
ｘ＝７

（４）
比例；ｙ＝ａｘ
10＝－２ａ
ａ＝－５
ｙ＝－５ｘ

（５）
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
１/４（２＋６）＝２

（６）
６個の玉から同時に２個取り出す組み合わせ→_６Ｃ_２＝15通り
【赤３個・白２個・青１個】
青を選んだ場合、あとは何を選んでも異色確定→赤or白の５通り
青を選ばなかった場合、赤と白の組み合わせ→３×２＝６通り
計11通りで、確率は11/15。

＠別解＠
余事象から全体－同色＝異色でも解ける。
赤₁・赤₂・赤₃から２個取り出す組み合わせ→取らない１個を選ぶ→３通り
白₁・白₂から２個取り出す組み合わせ→１通り
同色の組み合わせは計４通り。
異色は15－４＝11通りだから、確率は11/15。

（７）
ある式を□とする。
□＋（３ａ－５ｂ）をしたかったが、□－（３ａ－５ｂ）＝－２ａ＋４ｂをした。
（－２ａ＋４ｂ）＋（３ａ－５ｂ）をすると□が出て、
□＋（３ａ－５ｂ）をすれば正しい答えが出る。
ということは、（－２ａ＋４ｂ）に（３ａ－５ｂ）を２回足せばいい。

（－２ａ＋４ｂ）＋２（３ａ－５ｂ）
＝－２ａ＋４ｂ＋６ａ－10ｂ
＝４ａ－６ｂ

（８）

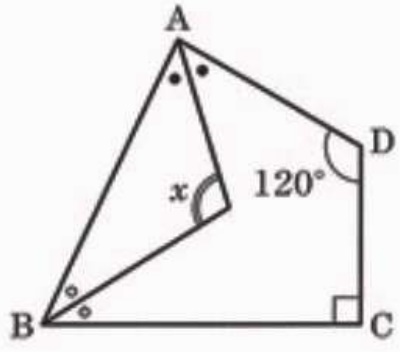
●●〇〇＝360－（120＋90）＝150°
●〇＝150÷２＝75°
ｘ＝180－75＝105°

（９）
810を素因数分解する。
810＝２×３⁴×５

異なる１桁の４つの素因数に分ける。
５を２倍すると９を超えてしまう→５は確定。
３の素因数が４つもある。３・３²＝９とバラす。
残りの３は２とくっつけて６にする。
３、５、６、９

（10）
【球の体積Ｖ＝４/３πｒ³】
円柱－球
＝２×２×π×４－４/３π×２³
＝16π－32/３π
＝16/３πｃｍ³

大問２（関数）

（１）
ｘ軸について線対称→上に凸のグラフに変わる。
ｙ＝－ｘ²

（２）
ｙ＝ｘ²にｘ＝２を代入、Ａ（２、４）
ｘ＝－３を代入、Ｂ（－３、９）
Ｂ（－３、９）→Ａ（２、４）
右に５、下に５だから傾きは－１。
Ａから左に２、上に２移動して、切片は４＋２＝６
ｙ＝－ｘ＋６

（３）

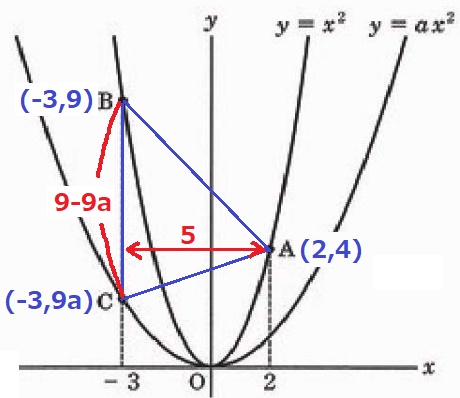
Ｃ（－３、９ａ）
△ＡＢＣの底辺ＢＣ＝９－９ａ、高さは２－（－３）＝５
面積は、（９－９ａ）×５÷２＝（45－45ａ）/２

（４）

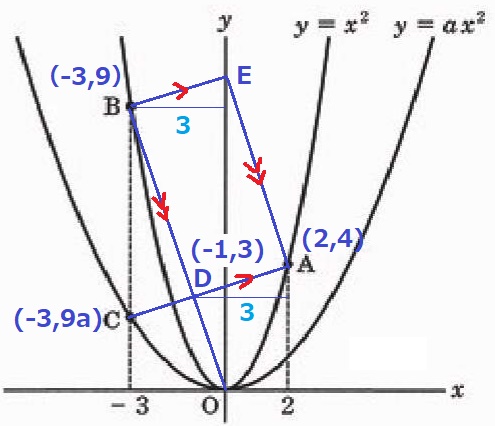
点Ｄ・Ｅを作図する。
Ｂ～Ｅ間のｘ座標の差が３→Ｄ～Ａ間も同様に３。
Ｄのｘ座標は、２－３＝－１

ＢＯの式；ｙ＝－３ｘ
ｘ＝－１を代入→Ｄ（－１、３）

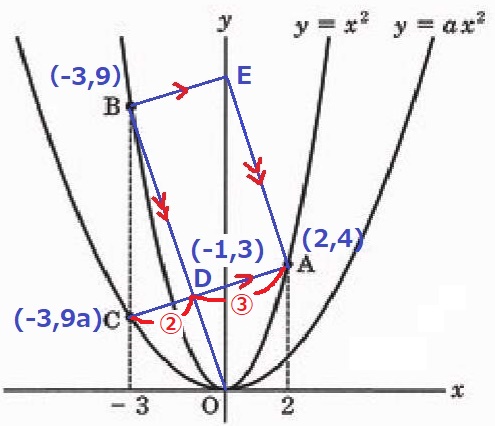
ｘ座標の差を取ると、ＣＤ：ＤＡ＝②：③
ＤとＡのｙ座標の差③＝４－３＝１
ＣとＤのｙ座標の差②＝１×②/③＝２/３
Ｃのｙ座標は、３－２/３＝７/３＝９ａ
ａ＝７/27

大問３（データの活用）

（１）①

４月１日以降の開花は８回。

②
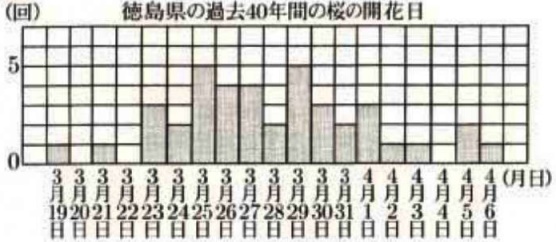
３月25～29日は、５＋４＋４＋２＋５＝20回
40年間の記録だから全体は40回。割合は20/40＝50％

（２）ａ

ア：最頻値（モード）は最もあらわれている値。図２…６日、図３…６日。×
イ：誤差０日はいずれも２回で同じ。〇
ウ：誤差10日以上は図２が５回、図３が３日。同じ40回の統計ゆえ、割合は図３が小さい。〇
エ：累積相対度数は、その階級以下の相対度数の合計。分母は一緒なので度数だけ数えればいい。
誤差３日以内は図２…２＋４＋５＋５＝16回、図３…２＋３＋５＋５＝15回。×
イ・ウ

ｂ
400℃の法則の方が誤差が小さい傾向にある理由を記述する。

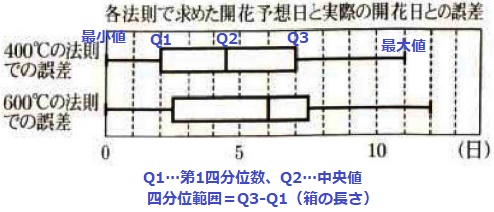
四分位範囲（箱の長さ）は400℃の方が微妙に左側にズレているが、
顕著な差がみられるのは中央値である。
データの半分が誤差０回（左側）に寄る400℃の方が正確な開花日を予想できる。

大問４（方程式）

（１）ａ

情報を表に書き込む。
入れ替え時間が最も短いのでこれをｘ分とすると、出し物は４ｘ分。
出し物は５つ、入れ替え時間はあいだの数で４つ。全体はAM10:00～PM0:00の120分。
４ｘ×５＋ｘ×４＝24ｘ＝120
ｘ＝５
出し物の時間は、４ｘ＝20
学級の出し物の時間…20分、入れ替えの時間…５分

ｂ
昼休み後はPM1:00～PM3:00の120分。
グループの発表時間は、（120－40）÷10＝８分

（２）ａ
昼休み以外の条件が変わる。ふたたび情報整理。

全体は15：20－９：40＝５：40＝340分
７ａ＋48＋60＋３ａ＋７ｂ＝340
10ａ＋７ｂ＝232

ｂ
前問の式にａ＝15を代入する。
10×15＋７ｂ＝232
７ｂ＝82
ｂ＝11.7…
最大で11グループ。

大問５（空間図形）

（１）
ねじれの位置→延長しても交わらない、かつ平行でもない。
正三角錐の６辺には平行がない。ＡＢと交わらないのはＯＣだけ。
辺ＯＣ

（２）
△ＯＡＤ∽△ＢＭＤの証明。

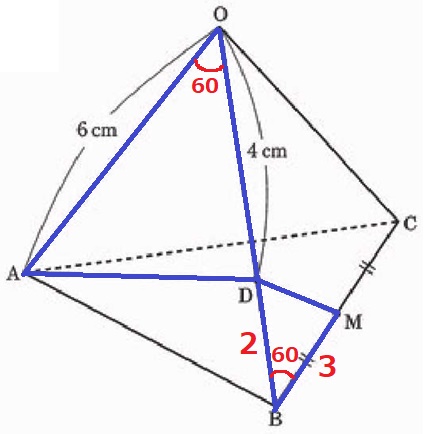
正三角形の内角より、∠ＡＯＤ＝∠ＭＢＤ
２つの三角形は同一面上にない。
ＯＡとＯＤの長さが出ているので、対応するＢＭとＢＤの長さを求めてみる。
ＢＭ＝６÷２＝３ｃｍ、ＢＤ＝６－４＝２ｃｍ
ＯＡ：ＢＭ＝６：３＝２：１
ＯＤ：ＢＤ＝４：２＝２：１
２辺の比とあいだの角が等しいから∽。

（３）

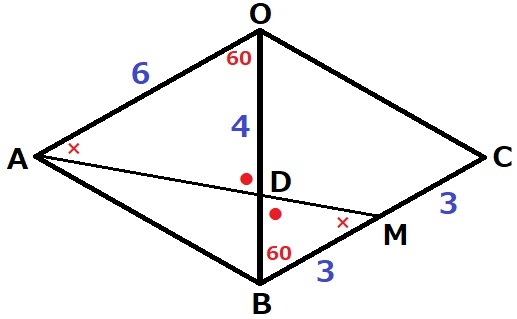
面ＯＡＢと面ＯＢＣを展開する。
前問の∽から、対応する∠ＡＤＯ＝∠ＭＤＢが等しい。
→対頂角が等しい→ＯＢは直線、ＡＭも直線である。
（ＯＢをＤを中心に回転するとＡＭになるイメージ）

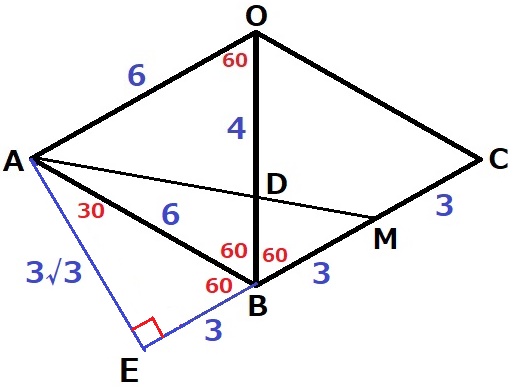
ＡＭを斜辺とする直角三角形をつくり、三平方からＡＭの長さを求める。
ＣＢを延長、Ａを通る垂線をおろして足をＥとする。
∠ＡＢＥ＝180－60×２＝60°
△ＡＥＢの内角は30°―60°―90°⇒辺の比は１：２：√３の直角三角形。
ＥＢ＝３ｃｍ、ＡＥ＝３√３ｃｍ
△ＡＥＭで三平方→ＡＭ（ＡＤ＋ＤＭ）＝３√７ｃｍ

（４）

立体をＡから眺めると見やすい。
Ａ―ＯＢＣ（全体）とＡ―ＯＤＰは高さが共通。
底面積の比である△ＯＢＣ：△ＯＤＰが２つの三角錐の体積比に相当する。

△ＯＢＣの面積を１とすると、△ＯＤＰは２/７。
１×②/③×ＯＰ/ＯＣ＝２/７
ＯＰ/ＯＣ＝３/７→ＯＰ：ＯＣ＝３：７
ＯＰ＝６×３/７＝18/７ｃｍ