2020年度　神奈川県公立高校入試過去問・追検査【数学】解説

問題はコチラ→ＰＤＦファイル
本検査はコチラ。昨年の残滓を感じる。

大問１（計算）

（ア）
－13＋５
＝－８　【３】

（イ）
－５/８－（－２/５）
＝－５/８＋２/５
＝－９/40　【３】

（ウ）
48ａ²ｂ÷６ａ
＝８ａｂ　【４】

（エ）
５/√６－√24＋√３/√２
＝５√６/６－２√６＋√６/２
＝－２√６/３　【１】

（オ）
（√２＋√７）（√２－√７）－３（√２－１）
＝（√２）²－（√７）²－３√２＋３
＝２－７－３√２＋３
＝－２－３√２　【２】

大問２（小問集合）

（ア）
0.1ｘ＋0.3ｙ＝－1.3　…①
１/５ｘ＋１/３ｙ＝－１…②

①を10倍、ｘ＋３ｙ＝－13…③
②を15倍して分母を払う。３ｘ＋５ｙ＝－15…④
③×３－④
３ｘ＋９ｙ＝－39
－)３ｘ＋5ｙ＝－15
４ｙ＝　－24
ｙ＝－６
③に代入。ｘ－18＝－13
ｘ＝５　【３】

（イ）
５ｘ²＋12ｘ＋２＝０
因数分解ができないので解の公式を適用。
ｘの係数が偶数なのでｂ＝２ｂ’が使える。
ｘ＝（－６±√26）/５　【１】

（ウ）
ｙの変域が正なので、傾きａは正（下に凸のグラフ）
原点を通過することに注意！
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－３のとき、最大値ｙ＝８
８＝（－３）²ａ
ａ＝８/９　【３】

（エ）
15Ｌに20ａを入れると、ｂＬ”より”多かった。
15＋20ａ＞ｂ　【２】

（オ）
√（67－３ｎ）が整数となる、正の整数ｎの個数を求める。
67－３ｎの値が平方数となれば根号が外れる。
67－３ｎ＝１
３ｎ＝66　ｎ＝22〇
67－３ｎ＝４
３ｎ＝63　ｎ＝21〇
67－３ｎ＝９
３ｎ＝58　ｎが正の整数にならない×
67－３ｎ＝16
３ｎ＝51　ｎ＝17〇
67－３ｎ＝25
３ｎ＝42　ｎ＝14〇
67－３ｎ＝36
３ｎ＝31　×
67－３ｎ＝49
３ｎ＝18　ｎ＝６〇
67－３ｎ＝64
３ｎ＝３　ｎ＝１〇
81は67を超えてしまうので終わり。
よって、６個　【４】

（カ）
60匹中８匹に印がついていた。
印付きの魚は全体で40匹なので、母集団は60×40/８＝300匹　【２】

大問３（小問集合２）

（ア）ⅰ
△ＡＢＥ∽△ＥＣＦの証明。

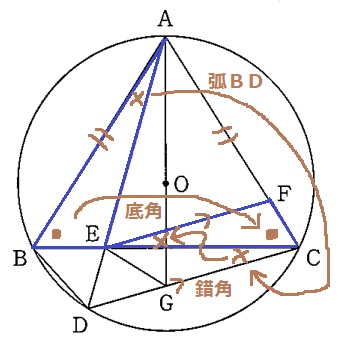
１つは、二等辺三角形ＡＢＣの底角。
もう１つは、弧ＢＤの円周角→錯角。
これで２角が等しいことになる。
ａ…２つの底角は等しい
ｂ…∠ＢＣＤ＝∠ＣＥＦ

ⅱ
最も出しにくい角度を求めます(´ﾟдﾟ｀)
ちょっと考えてダメだったら後回し推奨。

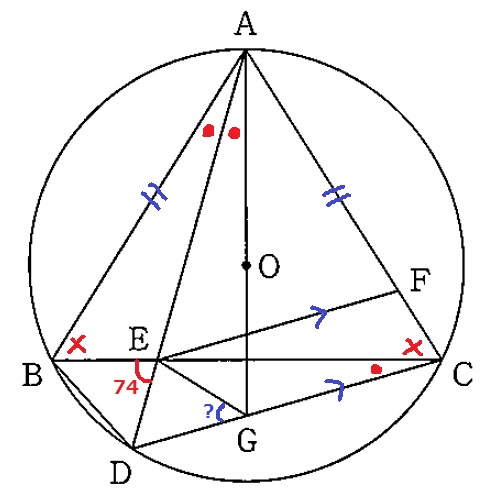
∠ＢＡＤ＝∠ＧＡＤ＝●とする。
弧ＢＤに対する円周角で、∠ＢＣＤ＝●
∠ＡＢＣ＝∠ＡＣＢ＝×とする。
△ＡＢＥの外角定理より、●＋×＝74°

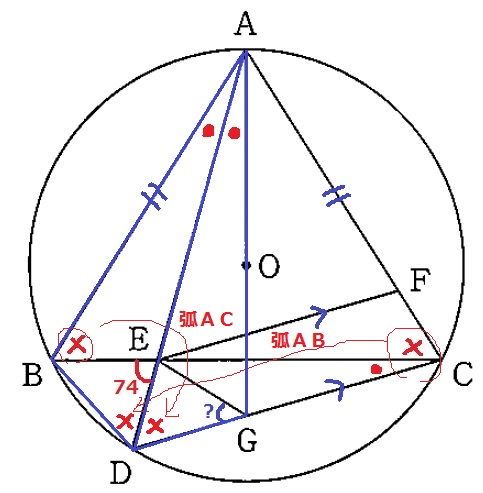
弧ＡＢと弧ＡＣに対する円周角から、∠ＡＤＢ＝∠ＡＤＣ＝×
△ＡＢＤと△ＡＧＤに着目すると、●＋×＋共通辺ＡＤより、
一辺両端角の相等から△ＡＢＤ≡△ＡＧＤ
ＡＢ＝ＡＧ

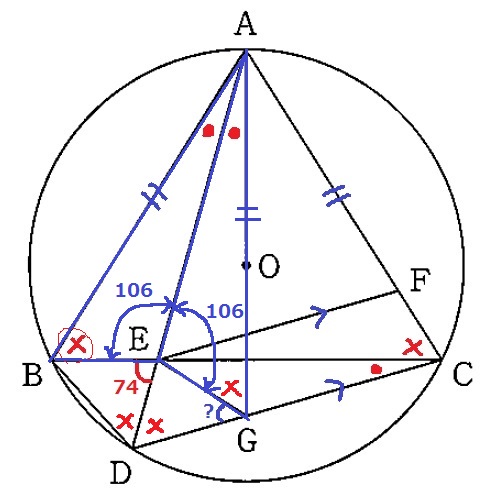
さらに、△ＡＢＥと△ＡＧＥで２辺とあいだの角が相等より合同。
△ＡＢＥ≡△ＡＧＥ
∠ＡＥＢ＝∠ＡＥＧ＝180－74＝106°

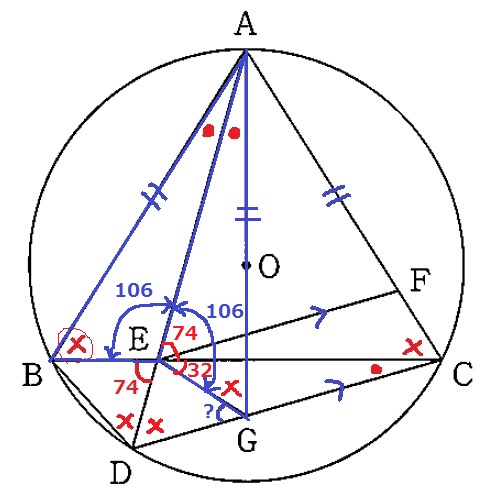
対頂角で、∠ＡＥＣ＝74°
∠ＣＥＧ＝106－74＝32°

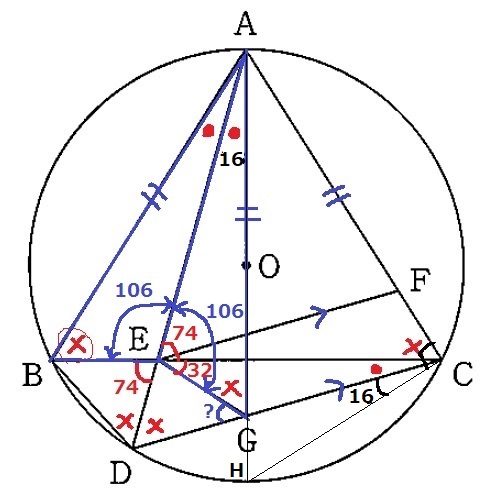
ＡＧを延長。円Ｏとの交点をＨとする。
直径に対する円周角から、∠ＡＣＨ＝90°
∠ＤＣＨ＝90－（●＋×）＝90－74＝16°
弧ＤＨに対する円周角から、∠ＤＣＨ＝∠ＤＡＨ
すなわち、●＝16°となる。
△ＥＣＧの外角定理から、∠ＤＧＥ＝32＋16＝48°

＠別解＠

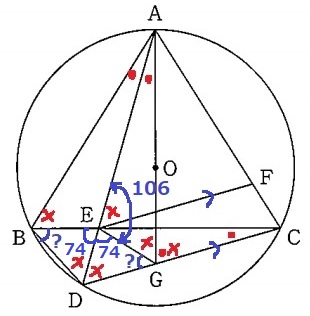
●＝16°、×＝58°さえわかれば、
△ＡＤＧの外角定理で、∠ＡＧＣ＝●＋×
∠ＤＧＥ＝180－（58＋74）＝48°

また、ＥＦ//ＤＣより、∠ＡＥＦ＝×＝58°
∠ＦＥＧ＝106－58＝48°
錯角で∠ＤＧＥ＝48°

さらに、△ＡＢＤ≡△ＡＧＤと△ＡＢＥ≡△ＡＧＥから△ＥＢＤ≡△ＥＧＤがいえる。
∠ＢＥＤ＝∠ＧＥＤ＝74°
△ＧＥＤの内角から、∠ＤＧＥ＝180－（58＋74）＝48°

＠別解２（追記）＠

等角はいろいろでてくるが、具体的な角度が74°しかわかっていない。
どこかで90°を見出さなければ答えが出せないと思われる。
求めたい角度は∠ＤＧＥで、ＡＧは直径の一部。
・・なんとなくＡＧとＢＣが直交してみえる…。

直径に対する円周角は直角。
△ＡＢＨと△ＡＣＨは、斜辺と他の１辺が等しい直角三角形で合同。
直径ＡＨを対称の軸とすると、ＢとＣは対応する点であり、
対応する点を結んだ線分と対称の軸は直交する。

弧ＡＣの円周角から、∠ＡＤＣ＝×
△ＡＤＧの外角定理で、∠ＡＧＣ＝●＋×＝74°
ＢＣとＡＧの交点をＩとし、△ＣＩＧの内角から、●＝180－（90＋74）＝16°と導ける。
先のように、△ＡＢＥ≡△ＡＧＥ→∠ＡＧＥ＝×とわかれば、∠ＤＧＥが求められる。
他に良い解法を見つけたかたはお問い合わせよりお知らせくださいませ。

（イ）
ここも難しい。
あ：最頻値は４日だったが、７→３に減ることで最頻値は変わってしまう。×
い：25人の中央値は、（25＋１）÷２＝13番目の値
修正前は４日の階級に中央値が含まれた。

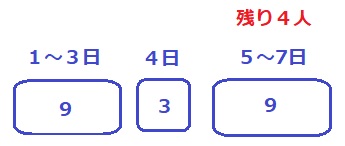
平均が変わらないように４人を配置する。
例えるならば、釣り合っている上皿てんびんが再び釣り合うように４つの分銅をのせていく。
わかりやすいのは真ん中の４を基準に＋１、－１、＋２、－２…
と対称的にのせていく方法だが、極端なケースを考えてみよう。
４日から－３（１日）に１つ、＋１（５日）に３つのせると、
１～３日の度数は10となり、中央値である13番目は４日になる。
反対に－１（３日）に３つ、＋３（７日）に１つのせると、
１～３の度数は12となり、中央値である13番目は４日なる。
すなわち、いかようにのせても中央値は変動しない！〇
う：－１（３日）と＋１（５日）に２つずつのせたり、
－２（２日）と＋２（６日）に２つずつのせれば１日は２人のまま。×
え：＋３（７日）に３つのせてしまうと、４未満の残り１つでは釣り合わない〇
おか：４つをのせるまえは、３日以下も５日以上も９つずつ。
　片方が10未満ということは、４つ全部を他方にのせることになるので釣り合わない〇
解答→い・え・お・か
*６つのうち４つを選ぶのには勇気がいるが完全解答です。

（ウ）
外側に相似図形を作るのだろうと方針は立てやすいが、計算処理が複雑。

ＢＦとＣＤを延長、交点をＨとする。
△ＡＢＦ∽△ＨＤＦより、ＨＤ＝③×１/２＝〇３/２
△ＥＢＧ∽△ＣＨＧより、ＢＧ：ＨＧ＝ＢＥ：ＨＣ＝②：〇９/４＝４：９
ＢＧ：ＧＨ＝④：⑨から、△ＢＣＨの面積を【13】とおくと、△ＢＣＧの面積は【４】。
△ＦＤＨ∽△ＢＣＨより、ＦＤ：ＢＣ＝１：３から、△ＦＤＨ：四角形ＢＣＤＦの面積比は１：８。
四角形ＢＣＤＦ＝【13】×８/９＝【104/９】
四角形ＣＤＦＧ（Ｔ）＝【104/９】－【４】＝【68/９】
よって、△ＢＣＧ（Ｓ）：四角形ＣＤＦＧ（Ｔ）＝【４】：【68/９】＝９：17

（エ）
一の位をｘすると、十の位は10－ｘ。
ある２桁の自然数をｘであらわすと、10（10－ｘ）＋ｘ
２文目から、これがｘ²－12と等しくなる。
10（10－ｘ）＋ｘ＝ｘ²－12　…ⅰ

うえの式を解く。
ｘ²＋９ｘ－112
＝（ｘ－７）（ｘ＋16）＝０
ｘ＞０より、ｘ＝７
一の位は７。
十の位は10－７＝３。
したがって、37　…ⅱ

大問４（関数）

（ア）
ｙ＝－１/４ｘ＋９にｘ＝４を代入。
Ａ（４、８）
これをｙ＝ａｘ²に代入。
８＝16ａ
ａ＝１/２　【４】

（イ）

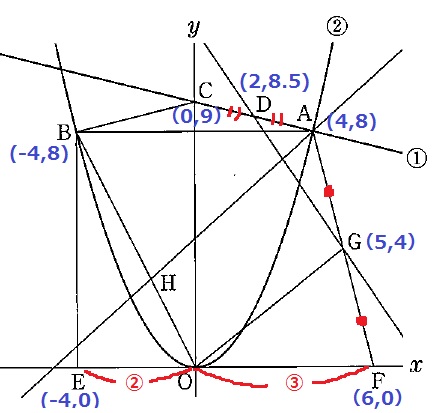
ＤはＡとＣの中点→Ｄ（２、8.5）
Ａ→Ｂ→Ｅ→Ｆ→Ｇと反時計回りに周回してＧ（５、４）
ＤとＧを通る直線の式を連立で求める。
8.5＝２ｍ＋ｎ　…①
－)４＝５ｍ＋ｎ　…②
4.5＝－３ｍ
ｍ＝4.5÷（－３）＝－３/２　…ⅰ【５】

①に代入。
8.5＝２×（－３/２）＋ｎ
ｎ＝11.5＝11と１/２＝23/２　…ⅱ【６】

（ウ）
等積変形を使ってＣやＧをＢＯ上にのせてもできると思うが、
五角形を分割するとありがたいことに、すべての面積が整数値になる。

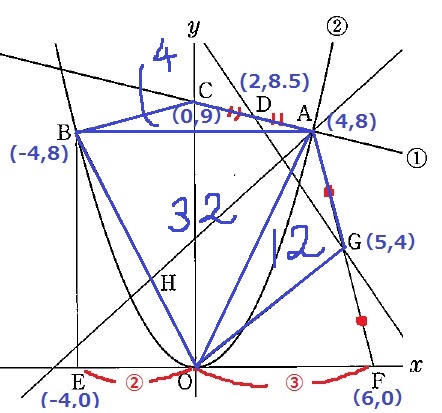
△ＡＢＣ…８×１÷２＝４
△ＡＢＯ…８×８÷２＝32
△ＡＯＧ…△ＡＯＦの半分なので、６×８÷２÷２＝12
五角形ＯＧＡＣＢの面積は、４＋32＋12＝48となり、その半分は24。

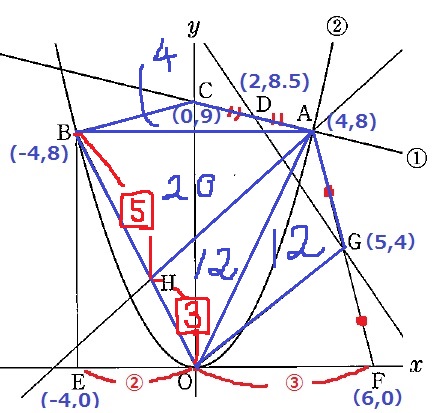
ＡＨが五角形を二等分するので、△ＡＢＨ＝20、△ＡＨＯ＝12
ＢＨ：ＨＯ＝20：12＝５：３
Ｈのｘ座標は、－４×３/８＝－３/２

ＢＯ：ｙ＝－２ｘだから、ｙ座標は－３/２×（－２）＝３
Ｈ（－３/２、３）

大問５（確率）

（ア）
全体の取り出し方は、４×３×３＝36通り
『６で引き分けになる』場合を考える。
Ａは６、Ｂは６を取り出す必要がある。
Ｃは何でもいいので３通り。
３/36＝１/12　【３】

（イ）
Ｂで場合分け。
◆Ｂが６を出す
Ａは６以外の３枚、Ｃは何でもいい。
３×３＝９通り

◆Ｂが５を出す
Ａは２か３、Ｃは３か４を出す。
２×２＝４通り

◆Ｂが１を出す
Ｂの敗北が決定。
したがって、確率は13/36
*確率は追試験の方が簡単だった。

大問６（空間図形）

（ア）

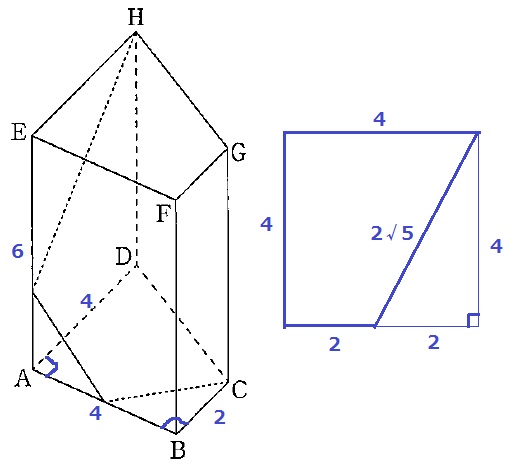
底面は台形。
ＤＣの長さは、うえのように三平方で処理して２√５ｃｍ。
（４＋２）×４÷２×２＋（４＋４＋２＋２√５）×６
＝24＋（10＋２√５）×６
＝84＋12√５ｃｍ²　【６】

（イ）
最短距離の問題なので展開図を作成。

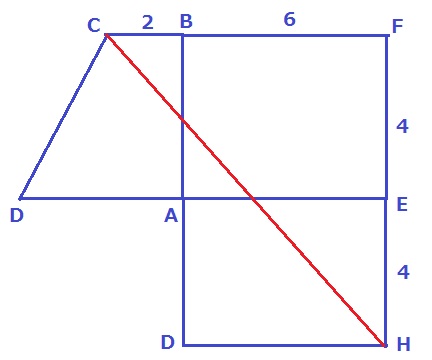
△ＣＦＨで三平方。
ＣＨ＝８√２ｃｍ　【２】
*△ＣＦＨは辺の比が１：１：√２の直角二等辺三角形。

（ウ）
むずい:(っ`ω´c):
底面を△ＢＥＩとしたときの高さがＦＪにあたる。
しかし、△ＢＥＩの面積を求めるのが至難…。
そこで、ＧＩ：ＩＨ＝１：２をヒントに外側に注意を向けてみる。

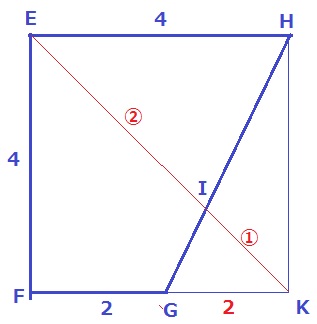
ＥＩとＦＧを延長、その交点をＫとする。
△ＥＨＩ∽△ＫＧＩより、ＥＨ：ＫＧ＝２：１
ＧＫ＝２ｃｍ
つまり、ＫはＨの真下にあり、四角形ＥＦＫＨは正方形となる。

ポイントは切断された部分を復元すること。
ＪＦは△ＢＥＫの高さでもある。
〔三角錘Ｂ－ＥＫＦの体積×３÷底面△ＢＥＫ＝高さＦＪ〕
三角錘Ｂ－ＥＫＦの体積…４×４÷２×６÷３＝16ｃｍ³

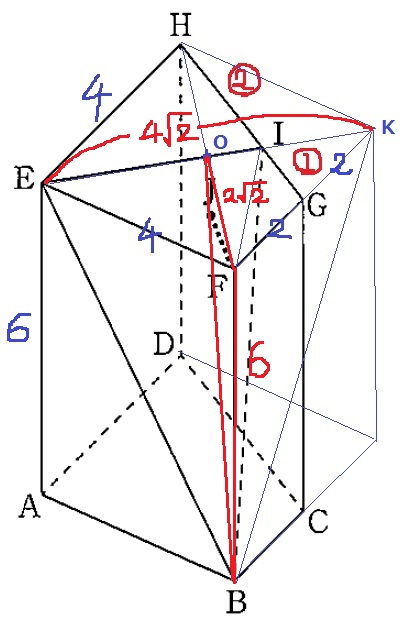
△ＥＫＦは直角二等辺三角形→１：１：√２ゆえ、ＥＫ＝４√２ｃｍ
対角線ＥＫとＨＦの交点をＯとする。
ＯＦ＝４√２÷２＝２√２
△ＯＦＢで三平方→ＯＢ＝２√11ｃｍ
△ＢＥＫ＝４√２×２√11÷２＝４√22ｃｍ

したがって、16×３÷４√22＝６√22/11ｃｍ

＠余談＠

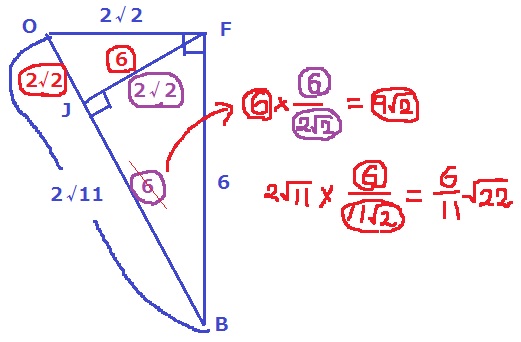
直角三角形ＯＦＢの３辺の長さがわかれば、相似図形で乗り越えられる。
ＯＦ：ＦＢ＝ＯＪ：ＪＦ＝ＦＪ：ＪＢ＝２√２：６
ＯＪ＝〇２√２、ＪＦ＝⑥とする。
ＪＢを〇で表すと、ＪＢ＝⑥×⑥/〇２√２＝〇９√２
ＯＢ＝〇２√２＋〇９√２＝〇11√２
２√11×⑥/〇11√２＝６√22/11ｃｍ

＠2020年度（神奈川）＠
数学…平均55.7点　社会…平均58.2点　理科…平均55.9点　英語…平均49.4点
その他は下記のリンクの目次からどうぞです。
公立高校入試解説ページに戻る