平均51.8点(前年比;-0.8点)

問題はこちら→兵庫模試さん(解答)
大問1(小問集合)
(1) 99.8%
3+(-7)
=3-7
=-4
(2) 94.1%
2(2x+y)-(x-5y)
=4x+2y-x+5y
=3x+7y
(3) 97.6%
2√3+√27
=2√3+3√3
=5√3
(4) 65.2%
9x2-12x+4
=(3x-2)2
(5) 76.8%
x2-x-4=0
解の公式を適用して、x=(1±√17)/2
(6) 84.7%
反比例の比例定数aは積xyで一定。
y=-9×2÷3=-6
(7) 87.1%
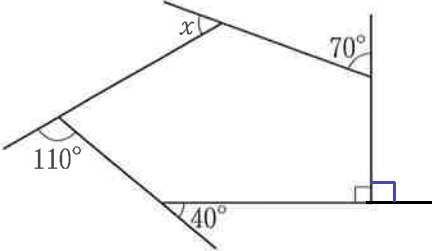
多角形の外角の和は360°だから、
x=360-(110+40+90+70)=50°
(8) 26.1%!

ア:平均点は×印などで示されるが、本問の箱ひげ図には記載がないので不明。×
60点は第2四分位数(Q2;中央値)である。
イ:四分位範囲=第3四分位数(Q3)-第1四分位数(Q1)
数学は80-50=30点、英語は70-45=25点で数学の方が大きい。〇
ウ:各生徒の数学と英語の得点はわからない。×
エ:数学のQ3が80点。35人のQ3は上位17人の真ん中、9番目の生徒が80点。〇
イ・エ
大問2(数量変化)
(1) 94.8%
980m÷14分=分速70m
(2) 44.0%
Bも980mを14分で歩くから分速70m。
→グラフの傾きは-70
y=-70x+bに(x、y)=(20、0)を代入。
0=-70×20+b
b=1400
y=-70x+1400
(3) 64.7%

Aの傾きは70、Bの傾きは-70。
傾きの絶対値が等しい→勾配(角度)が同じ→2つの底角が等しく、二等辺三角形。
交点のx座標は0~20分の真ん中の10分。
70×10=700m
(4) 13.0%!
Cをグラフに描く。

Cが出発した2分後の地点に図書館がある。
図書館はP地点から、300×2=600m
9時12分にAC間とBC間の距離が等しくなった⇒CはAとBの中間にいた。
AとBの勾配は同じだから、図の赤い三角形は横向きの二等辺三角形であり、
6~14分までのAとBの中間は700mラインである。
12分のときにCが700m地点にいればいい。
Cの移動時間は、700÷300=7/3分=2分20秒
図書館での滞在時間は、12分-2分20秒=9分40秒
大問3(平面図形)
(1)ⅰ…94.9%、ⅱ…91.9%
△ACE∽△ODEの証明。
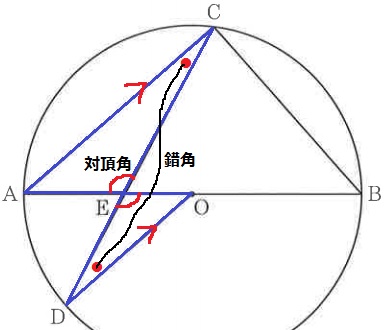
対頂角で、∠AEC=∠OED
AC//DOで錯角から、∠ACE=∠ODE
2角が等しいので相似。
ⅰ…ウ、ⅱ…オ
(2) 68.8%
△ABCで三平方→BC=2√7cm
(3) 11.9%!

半円の弧に対する円周角より、∠ACB=90°
(1)で証明した△ACE∽△ODEの相似比は6:4=3:2
AE=③、EO=②とおくと、半径でOB=OA=⑤
△ABCの面積を③/⑩倍すれば△ACEになる。
△ACEの面積は、6×2√7÷2×③/⑩=9√7/5cm2
(4) 2.0%!!
方べきの定理を使います。
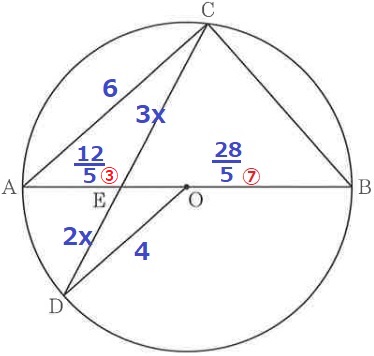
AE:EB=③:⑦なので、AE=8×③/⑩=12/5cm
EB=8-12/5=28/5cm
△ACE∽△ODEの相似比から、CE=3x、ED=2xとする。
方べきの定理より、【AE×EB=CE×ED】
12/5×28/5=3x×2x
6x2=(12×28)/25
x2=56/25
x>0だから、x=2√14/5
DE=2x=4√14/5cm
@@
地方テレビ?で放映された山本塾さんで素晴らしい解法が示されています。
DOを延長して中点連結定理を使うと良いそうです。
この古川先生というおっちゃん、話が面白くて気になります|ω・)
大問4(関数)
(1) 95.2%
y=1/2x2にx=2を代入する。
y=1/2×22=2
(2) 72.7%
y=ax2において、xの値がp→qに増加するときの変化の割合はa(p+q)
a(2+4)=3/2
6a=3/2
a=1/4
(3)① 40.9%
Dのx座標は-2
ABの傾きは3/2だから、Aから左に4、下に6移動するとE。
Eのy座標は、1-6=-5
E(-2、-5)
② 8.4%!!
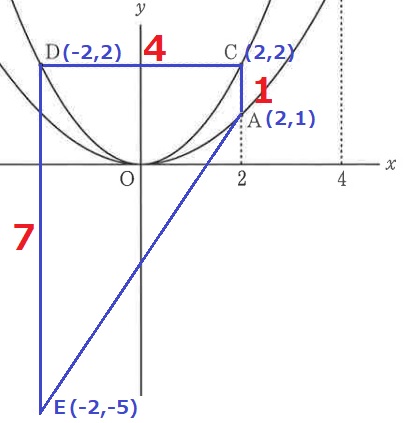
座標から長さを調べる。
AC=1、DE=7、CD=4

回転体は円錐台になる。
上の小さい円錐と全体の大きい円錐の相似比は1:7
小さい円錐の高さは、4×1/6=2/3cm
小さい円錐の体積は、1×1×π×2/3÷3=2/9πcm3
体積比は相似比の3乗。
小さい円錐:全体の円錐=13:73=1:343
求積すべき立体の体積は、小さい円錐を342倍すればいい。
2/9π×342=76πcm3
大問5(確率)
(1) 82.4%
オールB、オールC、オールDの3通り。
(2)① 50.3%
線分BCとなるには、BとCの2種類のカードを出す。
BとCは3つの袋に入っている。
(B、B、C)を入れ替えて3通り。
(B、C、C)を入れ替えて3通り。
計6通り
② 6.7%!!
ネジレの位置→平行でない、延長しても交わらない。
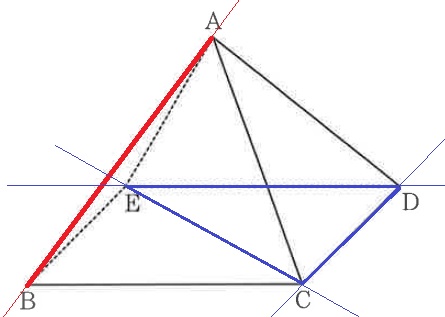
CDとDEだけでなく、CEもあることに注意!
正四角錐の辺だけとは限らない。
●線分CD
いずれの袋にもCとDはあるので、前問のBCと同じ6通り
●線分CE
Eは1つの袋しかない。
(C、C、E)の1通り
●線分DE
同様に1通り
計8通り
③ 4.0%!!

わかりやすいのは底面。
正方形BCDEの4つの頂点から3つを選べば2cm2の直角二等辺ができる。
Eの扱いに配慮するので、E無しかE有りで考える。
●E無し
B・C・Dはすべての袋に含まれる。
(B、C、D)の順列で3P3=6通り
●E有り
Eは1つの袋しかない。
(E、〇、〇)
〇はB~D
残りの袋でB・C・Dから2種類をとる。3P2=3×2=6通り
他にもないか調べてみる。
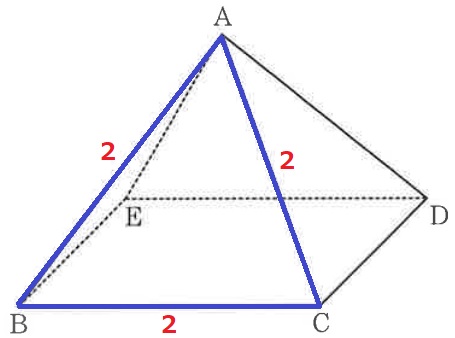
絶対違う。
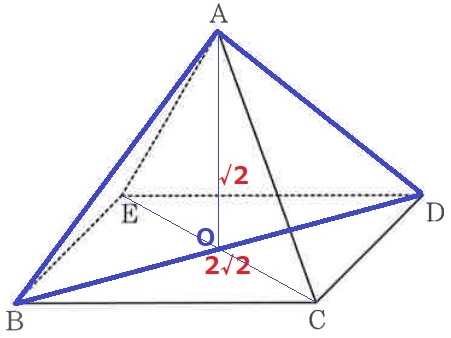
これが2cm2になってしまう。
直角二等辺BCDの辺の比は1:1:√2→対角線BD=2√2cm
Aの垂線の足をOとすると、△AOBなども直角二等辺でAO=BO=√2cm
△ABDの面積は、2√2×√2÷2=2cm2
(もしくは、△ABD≡△CBD=2cm2でもOK)
Aは1つの袋にしかないので(A、B、D)(A、D、B)の2通り
△ACEも2cm2だが、AとEは同じ袋にあるから同時にとることができない。
計14通り
全体は5×3×3=45通り
確率は14/45
大問6(整数)
(1) 96.7%
3×2×7=42
(2)① 70.9%
7つの平均値を出すのは面倒なので、
いずれの選手も3種目だからそれぞれの競技の順位を足して和を比較する。
最も和が小さいのは4位のナラサキ。
4位
*ナラサキ(楢崎智亜)は日本人の選手です→wiki
平均だったらトップだった。。
② 16.2%!
103=1000
10(10-n)(10+n)
=10(100-n2)
=1000-10n2
差は、1000-(1000-10n2)=10n2
③ 12.2%!
『nは0<n<10を満たす整数』だから、10n2にn=9を代入して、
10×92=810
(3) 7.4%!!
【A:4×〇×〇=401~410】
4×100=400だから、〇×〇=101か102
選手は20人なので、〇は20以下の数字である。
101=1×101
101は素数で20以下の組み合わせに分解できない→〇×〇=102
Aのポイントは4×102=408
102=1×102=2×51=3×34=6×17
20以下の組み合わせは6位と17位のみ。
【B:15×〇×〇=401~410】
400÷15=26.66…なので、Bのポイントは15×27=405
408>405だから、Aの選手が下位である。
A選手、6位と17位

昭和学院秀英でもスポーツクライミングのポイントを題材にした問題が出ました。
ぜひ挑戦してみて下さい。
●講評●
大問1
配点24点。死守したい。
大問2
(3)直感で二等辺三角形だと気づける。
AとBは同じ距離を14分で移動したから速さは同じ⇒傾きの絶対値が等しい。
二等辺の頂角の二等分線は底辺を垂直に二等分する。
(4)情報整理力が問われる。
12分後のCはどこにいるのか。ABの中点はグラフ上のどこにあるか。
Cの移動時間をひいて滞在時間を求める。
大問3
(3)相似比と半径でAE:EBが求まる。
(4)方ベキがデフォなの?と思ったが、中心Oと平行から中点連結定理は見えなかった。
古川先生に会いたい(˘ω˘)
CEを斜辺とする三平方もよぎったが、彼がおっしゃるように数値が汚く、ミスを招きやすい。

2020年・大阪B問題大問3(2)②イ(正答率0.4%)
形式は異なりますが、円の中心から補助線をひいて中点連結定理に持ち込む問題でした。
大問4
(3)体積比の処理に慣れておきたい。
小さい円錐の体積比が①なので、それの何倍かで円錐台がでる。
大問5
(2)②ひっかかる人が多そう。見えない線分に注意。
③正答率は低い。三角形は3種類ある。
AとEの処理が鍵。後回し推奨です。
大問6
(2)①いちいち÷3するのは重労働。合計を比較する。
③nの条件を思い出す。あらかじめ条件に線をひいておこう。
(3)内容は算数。選手は20人だから順位は20位まで。
20以下の数の組み合わせを探す。


コメント