2020年度　愛知県公立高校入試過去問Ａグループ【数学】解説

受検者平均10.8点（前年比；－1.9点）、合格者平均11.5点（前年比；－1.6点）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
３－４×（－２）
＝３＋８＝11

（２）
２/３（２ｘ－３）－１/５（３ｘ－10）
＝４/３ｘ－２－３/５ｘ＋２
＝11/15ｘ

（３）
（√10＋√５）（√６－√３）
＝√60－√30＋√30－√15
＝２√15－√15＝√15

（４）
２ｘ²＋５ｘ＋３＝ｘ²＋６ｘ＋６
ｘ²－ｘ－３＝０
因数分解できないので、解の公式を適用。
ｘ＝（１±√13）/２

（５）
５ｘ（ｘ－２）－（２ｘ＋３）（２ｘ－３）
＝５ｘ²－10ｘ－（４ｘ²－９）
＝ｘ²－10ｘ＋９
＝（ｘ－１）（ｘ－９）

（６）
クラスの人数をｘ人とする。
不足分は足し、超過分は引いて帳尻を合わせる。
300ｘ＋2600＝400ｘ－1200
100ｘ＝3800
ｘ＝38→38人

（７）
ｘ＝２のとき、ｙ＝３×２²＝12
ｘ＝４のとき、ｙ＝３×４²＝48
平均の速さ＝距離÷時間＝（48－12）/（４－２）＝毎秒18ｍ
*ｙ＝ａｘ²において、ｘの値がｐ→ｑまでの変化の割合はａ（ｐ＋ｑ）
３×（２＋４）＝毎秒18ｍ

（８）
全体の取り出し方は、５枚×４枚＝20通り
『積が奇数』→２つとも奇数の場合のみ。
Ａの箱から〔１・３・５〕Ｂの箱から〔１・３・５〕を取り出す。
３×３＝９通り
よって、９/20

（９）
接線と円の半径は直交する。

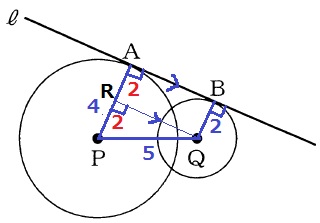
同位角が等しく、ＡＰ//ＢＱ
Ｑを通る、ＡＢに平行な線分を引き、ＡＰとの交点をＲとする。
（四角形ＡＢＱＲは４つの角度が90°で長方形）
ＡＲ＝ＲＰ＝２ｃｍ
△ＰＱＲで三平方→ＲＱ＝√21ｃｍ
ＡＢ＝√21ｃｍ

大問２（小問集合２）

（１）
式にあらわしてみよう。
ア＋（－５）＋２＝イ＋（－１）＋２＝ア＋１＋イ
ア－３＝イ＋１＝ア＋イ＋１

うしろの２つだけを抜き出すと、
イ＋１＝ア＋イ＋１　←イを消去
１＝ア＋１
ア＝０
前２つの式から、０－３＝イ＋１
イ＝－４

＠余談＠

左：アを含む２列は、ア以外の和が等しい。
右：イを含む２列は、イ以外の和が等しい。
魔方陣で使うテクニックです。

（２）
ａ：
平均値を求める。
（５×９＋４×９＋３×10＋２×６＋１×５＋０×１）÷40
＝128/40＝32/10＝3.2点

ｂ：
40人の中央値は、20番目と21番目の平均値。
いずれも３点にある→３点

ｃ：
配点は第１問が１点、第２問と第３問が２点。
第１問を正解した合計人数は奇数点になる。
よって、９＋10＋５＝24人

ｄ：
３問正解した人は５点→９人
２問正解した人は４点と３点→19人
１問正解した人は２点と１点→11人
（３×９＋２×19＋１×11）÷40＝76/40＝19/10＝1.9問

（３）
ｙ＝２/ｘからＡ（１、２）、Ｂ（３、２/３）

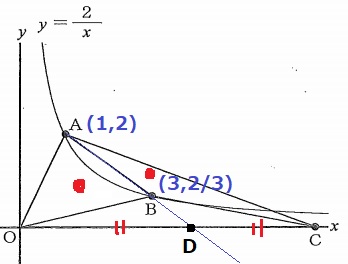
△ＡＯＢと△ＡＢＣの面積が等しいということは、
共通辺ＡＢを底辺としたときの高さの比が等しい。
ＡＢを延長してｘ軸との交点をＤとすると、ＯＤ＝ＤＣとなる。

ＡとＢを通る直線の式を連立で求める。
２＝ａ＋ｂ…①
－)２/３＝３ａ＋ｂ…②
４/３=－２ａ
ａ＝－２/３
①に代入。２＝－２/３＋ｂ
ｂ＝８/３
ｙ＝－２/３ｘ＋８/３

ｙ＝０を代入。
０＝－２/３ｘ+＋８/３
ｘ＝４
Ｄ（４、０）ゆえ、Ｃ（８、０）

＠別解＠
Ｂのｙ座標がやらしい。
２：２/３＝３：１を見出せれば、相似図形でも攻略可。

Ｄのｘ座標…２×③/②＋１＝４

（４）①

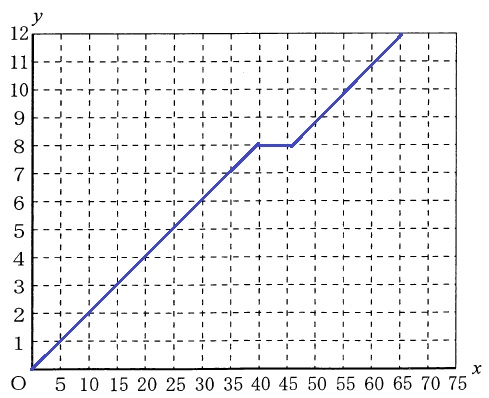
Ａは時速12ｋｍで進む。
グラフで60分・12ｋｍの点と原点を結ぶと、傾きがちょうど45度線。
原点から45度にｙ＝８ｋｍまで線分をひき、５分休憩、そこから45度線。

②

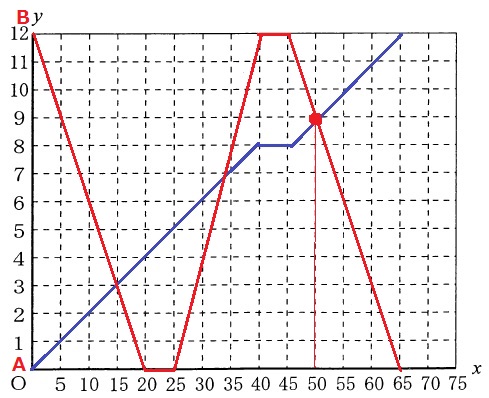
バスはＢ地点から出発する。
Ｂ→Ａ；時速48ｋｍ、Ａ→Ｂ；時速36ｋｍと変速するので注意！
正しく作図できれば、出会った時間の計算は不要。
50分後

大問３（図形）

（１）

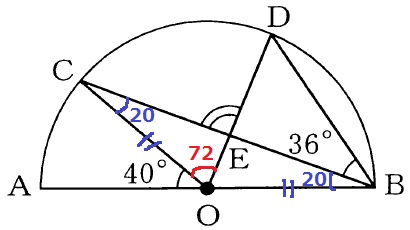
半径より、△ＢＯＣは二等辺→∠ＯＢＣ＝∠ＯＣＢ
△ＢＯＣの外角定理から、∠ＯＣＢ＝40÷２＝20°
∠ＣＯＤは円周角ＣＢＤの中心角で、36×２＝72°
△ＣＯＥで外角定理→∠ＣＥＤ＝20＋72＝92°

（２）①

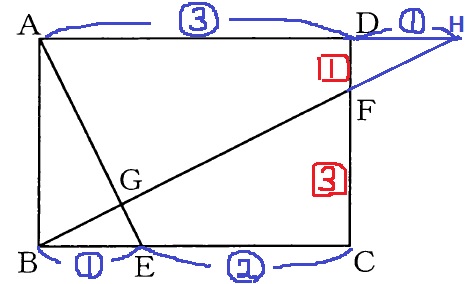
ＡＤとＢＦを延長、交点をＨとする。
△ＢＣＦ∽△ＨＤＦより、ＤＨ＝③×１/３＝①
△ＡＧＨ∽△ＥＧＢより、ＡＧ：ＥＧ＝ＡＨ：ＥＢ＝４：１
よって、ＡＧはＧＥの４倍。

②
本試験最大の難所。

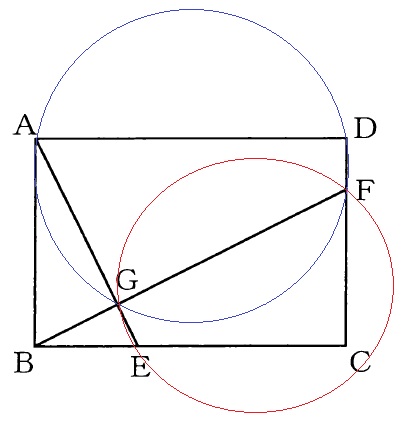
こんな感じで円が２つできるという。
求めたいのは円の面積比。
半径の２倍が直径なので、直径の比さえわかればその２乗で決着がつく。
では、円の直径はどこにあるのだろう？

入試問題にでてくる問題では、たいてい変な場所に中心点はない！
中心は円の直径にある。
円…直径…半円の弧に対する円周角は90°…
どこかの角が90°であれば、円の直径が特定できる。

問題文の図をパッと見て、ＡＥとＢＦが直交しているように見える。
幾何ではこういった勘は大切です。
△ＡＢＥと△ＢＣＦを調べると、
ＡＢ：ＢＥ＝４：２＝２：１
ＢＣ：ＣＦ＝６：３＝２：１
２辺の比と間の角が等しいので、△ＡＢＥ∽△ＢＣＦ

●＋×＝90°で対応する角に印をつけると、∠ＢＧＥ＝90°を認定。
やはり、ＡＥとＢＦは直交していた。
次に、90°を円周角とする直径を探す。

ＡＦとＥＦに補助線。
∠ＡＧＦを円周角とする直径ＡＦ、∠ＥＧＦを円周角とする直径ＥＦ。
円の中心はＡＦとＥＦの中点に隠れていた。
また、長方形の内角から∠ＡＤＦ＝△ＥＣＦ＝90°なので、
つまるところ、Ａ・Ｇ・Ｆ・ＤとＥ・Ｇ・Ｆ・Ｃの４点はそれぞれ同一円周上にある。

△ＡＤＦで三平方→ＡＦ＝√37
Ｏ₁直径＝√37ｃｍ
△ＥＣＦで三平方→３：４：５より、ＥＦ＝５
Ｏ₂の直径＝５ｃｍ
円の面積比は直径の２乗だから、
（√37）²：５²＝37：25
したがって、37/25倍

（３）①

正方形ＡＢＣＤの対角線の交点をＨとする。
△ＡＢＣで三平方→１：１：√２よりＡＣ＝６√２
ＡＨ＝６√２÷２＝３√２
△ＡＯＨで三平方→ＯＨ＝３√７
体積は、６×６×３√７÷３＝36√７ｃｍ³

②
空間で距離ときたら『高さ』
底面ＯＢＣからＡまでを高さとする立体を捉える。

留意点は、△ＯＢＣをゴロンと傾けて床につけたとき、
Ａまでを高さとする立体は三角錐Ａ－ＢＯＣ。
これは正四角錘Ｏ－ＡＢＣＤの体積の半分である18√７ｃｍ³である。
△ＯＢＣの高さは三平方で６√２ｃｍ、面積は６×６√２÷２＝18√２ｃｍ²
よって、求める高さは18√７×３÷18√２＝３√14/２ｃｍ

大問１
計算問題はすべて死守！
（９）円や扇形がきたら半径作図。
大問２
（１）経験の差がでやすい。
（２）後半に推論要素が含まれる。ｃ『各問題の配点をあわせて考えること』がヒント。
（３）中受の算数にでてくるベンツ切りみたいな。
（４）なるべく時間をかけたくない。
大問３
（２）②シンプルisディフィカルト(;´･ω･)
円の面積比→直径→半円の弧に対する円周角は90度。
90度の捜索に２辺の比とあいだの角を相似条件とした相似図形を見つける必要がある。
（３）②ここもひっかかりやすい。底面をＢＯＣ→ＡＢＣと視点を切り替えると正四角錘の半分。
公立高校入試解説ページに戻る