平均55.7点(前年比;+5.4点)

問題PDF
2020年度神奈川追検査の解説はコチラ。
大問1(計算)
(ア) 92.8%
2-(-9)
=2+9
=11 【4】
(イ) 97.4%
52a2b÷(-4a)
=-13ab 【2】
(ウ) 95.5%
√28+49/√7
=2√7+7√7
=9√7 【2】
(エ) 85.0%
(3x-y)/3-(x-2y)/4
={4(3x-y)-3(x-2y)}/12
=(12x-4y-3x+6y)/12=(9x+2y)/12 【4】
(オ) 91.0%
(√2+1)2-5(√2+1)+4 ←√2+1をXに置き換える
=X2-5X+4
=(X-1)(X-4) ←Xを戻す
=(√2+1-1)(√2+1-4)
=√2(√2-3)=2-3√2 【1】
大問2(小問集合)
(ア) 90.9%
x=2、y=1を代入。
2a+b=10 …①
2b-a=5 …②
②より、a=2b-5
①に代入。2(2b-5)+b=5b-10=10
b=4
a=2×4-5=3 【2】
(イ) 90.5%
x2-5x-3=0
解の公式を適用して、x=(5±√37)/2 【4】
(ウ) 83.3%
x=3のとき、y=-3
x=6のとき、y=-12
変化の割合=(yの増加量)/(xの増加量)
={-12-(-3)}/(6-3)=-3 【2】
@@
もしくは、y=ax2において、p→qまでの変化の割合はa(p+q)だから、
-1/3(3+6)=-3
(エ) 82.7%
子ども1人の入園料をxとすると、大人1人はx+600円。
x+600:x=5:2
内項と外項の積より、5x=2(x+600)
3x=1200
x=400 【1】
(オ) 72.3%
5880を素因数分解すると、5880=23×3×5×72
平方数にしたいので、2と3と5を1個ずつ抜き取れば、
22×72(=196)と14の平方数になる。
2×3×5=30 【3】
*数字が4つしかないので、わからなかったら全部試せる。
(カ) 52.5%
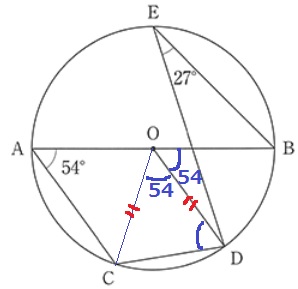
∠BOD=27×2=54°
∠BOC=54×2°なので、∠COD=54°となる。
半径から△OCDは二等辺。
∠ODC=(180-54)÷2=63° 【2】
大問3(小問集合2)
(ア)ⅰ a:93.5% b:88.9%
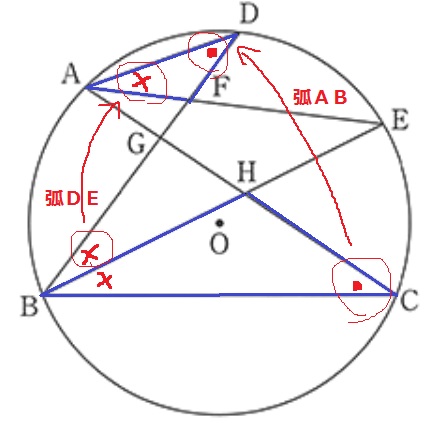
証明としては基本レベル。
a:∠ADB=∠ACBが等しい理由は、弧ABに対する円周角。【1】
b:BEが角の二等分線なので、∠CBE=∠DBE。【3】
ⅱ 39.1%
AとBを含む同一円周上にある他2点を求める。
円Oと異なるので、円O上にあるC・D・Eが外れる。
なぜなら、たとえばA・B・C3点が円周上にくる円は円Oただ1つしかないから。
(1つしかないからこそ、3点を通過する円の作図問題がでてくる)
GはA・Bに近すぎて、もう1つの点がきにくい。ということは、F・Hが怪しい。
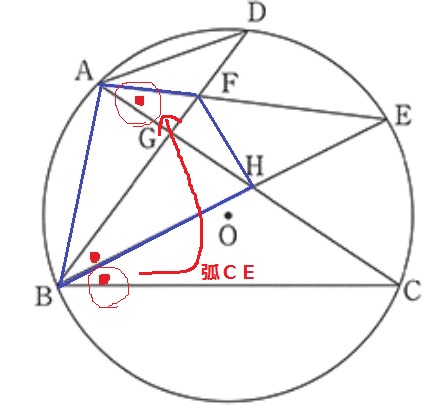
弧CEに対する円周角で●を移動。
円周角の定理の逆から、『直線FHに対して2点A、Bが同じ側にあり、
∠FAH=∠FBHが成り立つので、4点A・B・H・Fは同一円周上にある』
点Fと点H
(イ)ⅰ:40.7% ⅱ:54.9%
以下、説明文を上から順に①~⑥とする。
①1月はB・C・E・F
②1月はうえの4つのうち、B・E・Fに絞られる。
次に④をみる。④から1月と11月はCとFではない。
→1月はBかE
③6つのうち1月の平均値は2番目に高かった。
ここで6回も平均値の計算を強いるのであればクソ問題認定だが、本問は予想はできる。
全体を俯瞰して、データが右側に寄っているAが最も平均値が高いはず。
2番目に平均値が高い1月はBかEなので、どちらの平均値が高いかといえば、
6~8℃の階級を真ん中にみて、右側にデータが偏るEが2番目に大きい平均値となるはず。
1月はE
⑤11月はB~F
⑥11月はCかD
④と⑥をあわせると、11月はDと確定。
ⅰ:【5】 ⅱ:【4】
(ウ) 5.1%!!
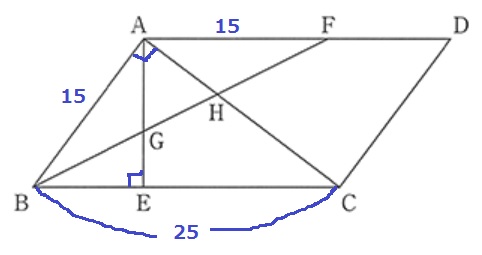
△AHF∽△CHFより、
FH:BH=AF:CB=15:25=3:5
さらに、直角三角形ABCの斜辺が25で最も短い辺が15cm。
ここから△ABCは3:4:5の直角三角形とわかる。
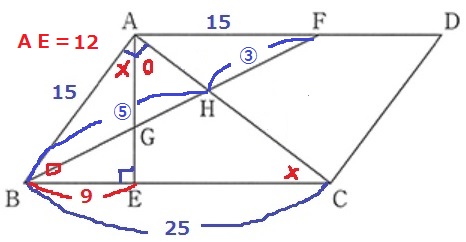
直角三角形の内部に直角三角形のスタイルなので、〇+×=90°で角度調査を行うと、
△ABEの内角も〇-×-90°となり、辺の比が3:4:5。
BE=15×3/5=9cm、AE=15×4/5=12cm
B-G-H-Fで連比処理。
BG:GF=9:15=3:5
BH:HF=5:3
ありがたいことに比の和であるBFがともに8なので、そのまま比を統一できる。
BG:GH:HF=3:2:3

△ABF→△AGH
15×12×1/2×2/8=45/2cm2
(エ) 20.8%!
歯車→反比例
ⅰ:24×6÷36=4回転
ⅱ:反比例の式を記述する。
比例定数a=24×6=144
y=144/x
大問4(関数)
(ア) 89.0%
y=xより、A(6、6)
これをy=ax2に代入。
6=36a
a=1/6 【3】
(イ) 49.7%
AO:OE=4:3より、6×3/4=9/2
E(-9/2、-9/2)
y=-x+3とx軸との交点。
F(3、0)
2点を通る連立方程式を解く。
-9/2=-9/2m+n…①
0=3m+n…②
①-②…-9/2=-15/2m
m=3/5 ⅰ…【4】
②…0=3/5×3+n
n=-9/5 ⅱ…【3】
(ウ) 3.9%!!
△ADGと四角形BEDCの面積比を求めたいので、これらの頂点座標を確定しておく。
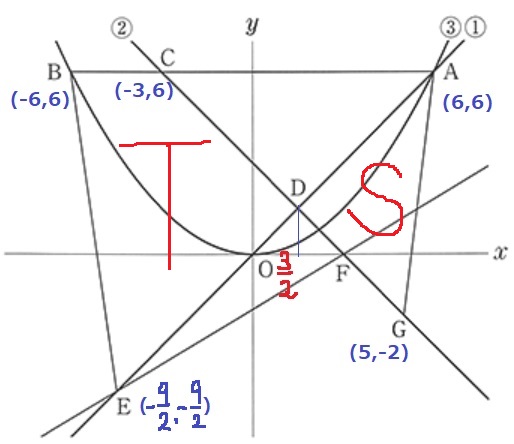
CとGはy=-x+3から導く。
Dは、y=xとy=-x+3の交点なので、
x=-x+3
x=3/2
D(3/2、3/2)
複雑な図形は共通部分を巻き込み、整った図形に変える。
△ACDを巻き込んでみよう。
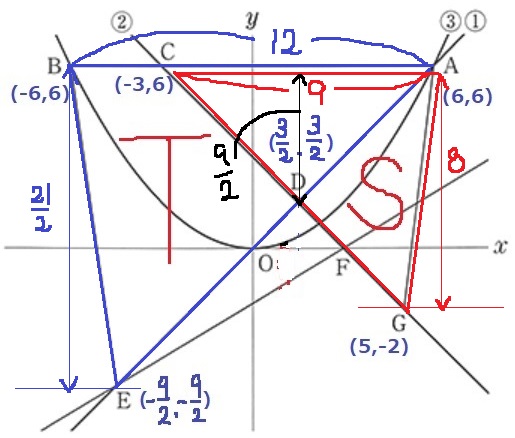
ごちゃごちゃして申し訳ない。。
T=△ABE-△ACD
S=△ACG-△ACD
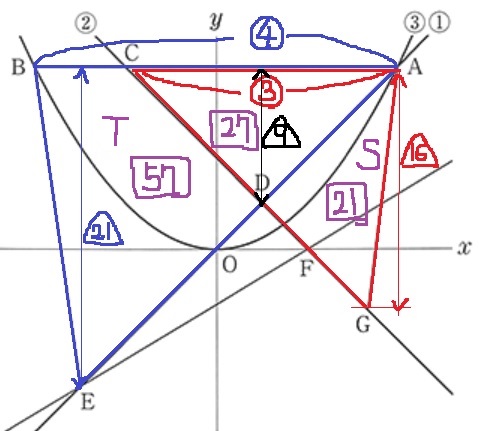
底辺…9:12=③:④
高さ…21/2:9/2:8=△21:△9:△16
△ACD=③×△9=【27】
△ADG(S)=③×(△16-△9)=【21】
四角形BEDC(T)=④×△21-【27】=【57】
S:T=【21】:【57】=7:19
大問5(確率)
(ア) 66.8%
袋からの取り出し方は6×6=36通り
平面ABCD上の点は(B,C)(B,D)(C,D)とこれらの逆。
計6通り
6/36=1/6 【6】
(イ) 12.3%!
方針としては、等辺から攻めて全体から引くか、不等辺三角形を直接数えにいくか。
等辺だと、たとえば二等辺三角形であれば、どことどこが等辺の組み合わせになるかで
いろいろパターンがでてくるので整理しづらい。
そこで不等辺三角形をチョイスする。
立方体内部にできる三角形で3辺がすべて異なるようにするには、
〔正方形の1辺+正方形の対角線+立方体の対角線〕
とりわけ、立方体の対角線は4本しかないのでココに狙いを定める。
◆対角線AG
残り1つの頂点はどこでもいい。
袋から、Gと(B・C・D・E・F)を取り出す。
袋Pと袋Qの逆を含めて10通り。
また、(G、G)で△AGHが作られるので計11通り
◆対角線EC
(E、C)(C、E)の2通り
◆対角線DF
同様に2通り
◆対角線HB
(B、B)しかない。
これらをあわせて16通り
16/36=4/9
大問6(空間図形)
(ア) 50.6%
四角形ABCDは正方形。
三角形ADEは正三角形で高さは3√3cm。
6×6+6×3√3÷2=36+9√3cm2 【6】
(イ) 34.6%
立体図がない。
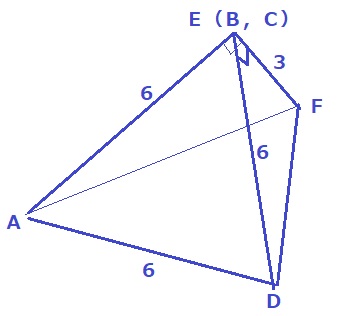
↑△ADFを底面にして組み立てるとこうなる。
似たような三角形なので頭の中が混乱しやすい。
△ADEは正三角形だけど、△ADFは二等辺三角形。
体積を求めるときは△ADEを底面にすると、高さはEFになる。
9√3×3÷3=9√3cm3 【5】
(ウ) 0.5%!!!
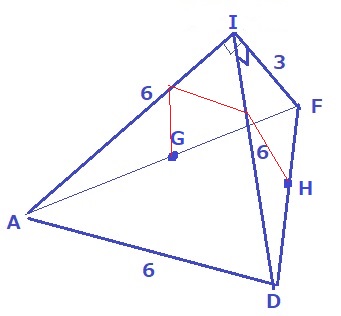
うえのような感じでヒモをひっかける。
最短距離なので展開図を作成。
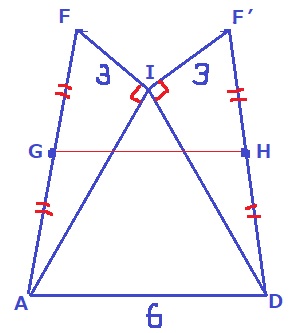
GHを1辺とした三平方…は使えないので、別の手法を探す。
困ったら角度を調査しよう。
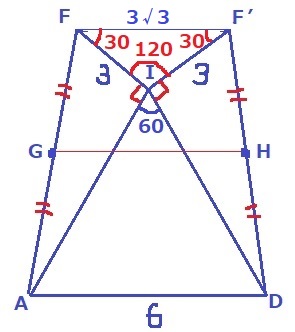
∠FIF’=360-(90×2+60)=120°
△IFF’は二等辺三角形なので、内角は30°-30°-120°
縦に真っ二つに切ると1:2:√3の直角三角形になるから、
FF’=3×√3/2×2=3√3cm
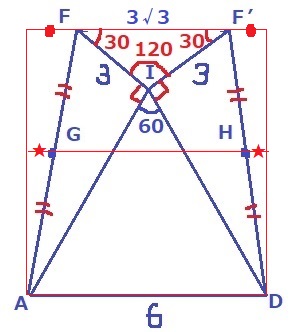
●●=6-3√3
左右の三角形に中点連結定理を一括適用。
★★=(6-3√3)÷2=3-3√3/2
GH=6-★★=6-(3-3√3/2)=3+3√3/2cm
@別解@
最後は、(AD+FF’)÷2=(6+3√3)÷2=3+3√3/2cmでもいける。
GとHはAF、DF’の中点にあり、平行線と線分の比を用いる際に、
”GHはADとFF’の平均である”と考えれば、イメージしやすいんじゃないかな?



コメント