平均27.1点(満点50点、前年比;+0.6点)
問題はこちら→東進ハイスクールさん(解答)
2020年度・三重前期(数学)解説は別ページ。
大問1(計算)
(1)
(-9)×7
=-63
(2)
4/5x-3/4x
=1/20x
(3)
7(a-b)-4(2a-8b)
=7a-7b-8a+32b
=-a+25b
(4)
(√5-√2)2
=5-2√10+2
=7-2√10
(5)
x2-36
=(x+6)(x-6)
(6)
x2+5x-1=0
因数分解ができないので解の公式を適用。
x=(-5±√29)/2
(7)
総和=平均×個数
合計の冊数=5.5×6=33冊
5+4+3+7+n+5=33
n=9
大問2(小問集合)
(1)①
18000円+600円×15冊=27000円
②ア
y=600x+18000
yに40000を代入。
40000=600x+18000
x=36.6…
36.6…冊で総費用が4万円なので、4万円以内では最大36冊刷れる。
36冊
(*1次不等式でいえば、y≧600x+18000)
イ
A社は初期費用が無料で、文集1冊あたり1250円かかる。
→原点を通る比例で、傾きは1250。
y=1250x
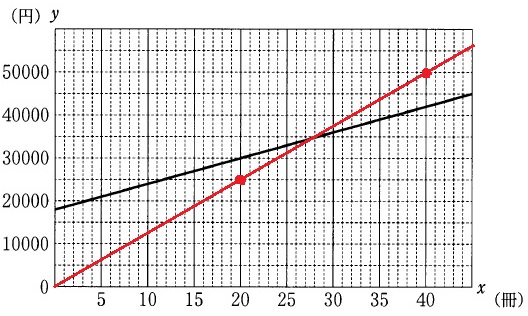
グラフは格子点を意識しよう。
y軸は5000刻みなので、yの値が5000の倍数となるところを探す。
x=20のとき、y=25000(20、25000)
x=40のとき、y=50000(40、50000)
原点とこれらをつなぐように描く。
ウ

交点のx座標が正解。なんとなく28冊に見える…。
試しに計算すると、
600x+18000=1250x
x=27.6…
27冊ちょっとでA社とB社の金額が同じになるので、28冊以上でB社が逆転して安くなる。
28冊以上
(2)
連立方程式。
距離の等式
x+y=1800…【1】
時間の等式
x/60+y/160=20…【2】
②を480倍して分母を払う。
8x+3y=9600…【3】
【3】-【1】×3をすると、5x=4200
x=840
【1】より、y=1800-840=960
①…x+y、②…x/60+y/160、③…840、④…960
(3)①
素数は規則性がないので、1個ずつ調べるしかない。
m→11、13、23、31、41、43、53、61
計8通り
8/36=2/9
②
√mが自然数になるということは、mは2桁の平方数。
m→16、25、36、64
計4通り
4/36=1/9
大問3(関数)
(1)
y=3x+7にx=-2を代入。
A(-2、1)
これをy=ax2に代入。
1=(-2)2a
a=1/4
(2)
x=0のとき、最小値y=0
x=3のとき、最大値y=1/4×32=9/4
0≦y≦9/4
(3)①
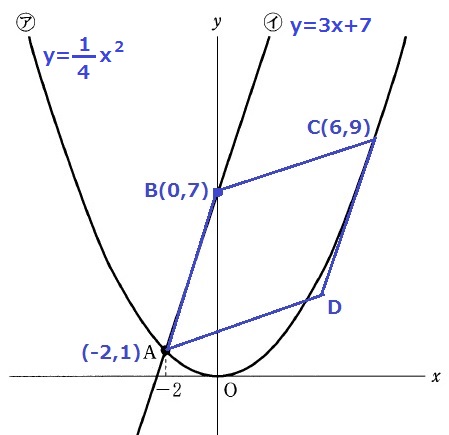
まずはD以外の座標を確定しよう。
Bはイの切片、Cはx=6をアに代入。
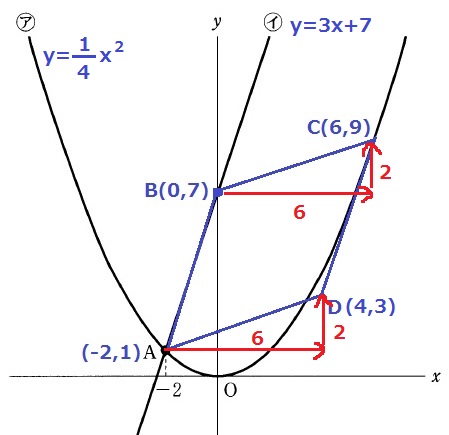
四角形ADCBが平行四辺形であることは利用する。
B→Cは右に6、上に2。
A→Dも同様。Aから右に6、上に2移動して、D(4、3)
②
平行四辺形ADCBを2等分する直線は平行四辺形の中心を通る。
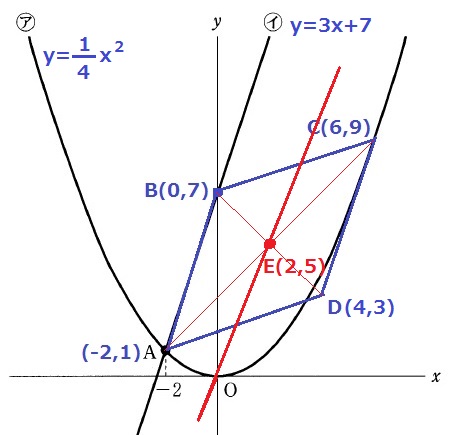
対角線ACとBDの交点をEとおく。
Eのx座標は4と0の平均、y座標は9と1の平均→E(2、5)
あとはOEの式を求めればいい。
y=5/2x
大問4(空間図形・作図)
(1)①
底面の△BCDは正三角形。
BFは正三角形を真っ二つにする。
△BCFは1:2:√3の直角三角形なので、
BF=6×√3/2=3√3cm
②
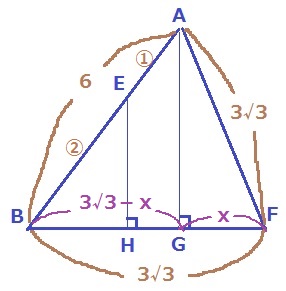
△ABFでとらえる。
AFもBFと同じ、正三角形の中線で3√3cm
AとEのそれぞれの足をG、Hとする。
GF=xとおくと、BG=3√3cm
△ABGと△AFGで三平方をする。
AB2-BG2=AG2=AF2-FG2
62-(3√3-x)2=(3√3)2-x2
6√3x=18
x=√3
△AFGで三平方→AG=2√6cm
△ABG∽△EBHから、AG:EH=3:2
よって、EH=2√6×2/3=4√6/3cm
@別解@
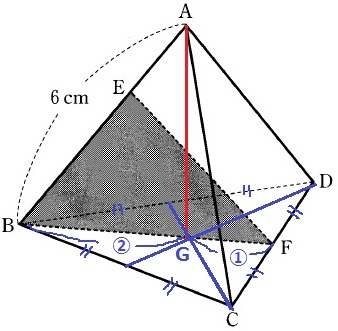
Gは△BCDの重心に相当する。
Gは中線BFを2:1に内分する。
これを知っていれば、BG=3√3×2/3=2√3cm
△ABGで三平方→AG=2√6cmとすぐでる。
(2)
辺BCと辺ADに接する円の中心点はどこにあるのだろう?
まずは中心点を含む線分を考える。
円の半径は等しく、かつ半径と接線は直交する→中心点は2つの辺から等距離にある。

ポイントは、ADをBCを延長すること。
交点をEとして、∠AEBの二等分線上に中心点がある。
これとABとの交点が求めるべき円の中心点。
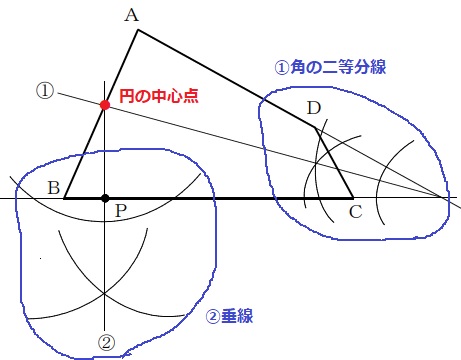
①角の二等分線の作図
②垂線の作図
BCとの交点がPとなる。
大問5(平面図形)
(1)
△AHC∽△CJIの証明。
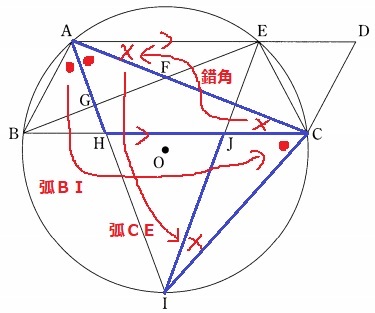
複雑な図形だが、誘導付きなのでありがたい。
円周角の定理&平行線からの錯角を利用。
ア:∠HAB、イ:∠CAE、ウ:2組の角
イは∠CADも錯角になるが、次に弧CEに対する円周角がでてくるので∠CAEが良い。
(2)
△ADC≡△BCEの証明。
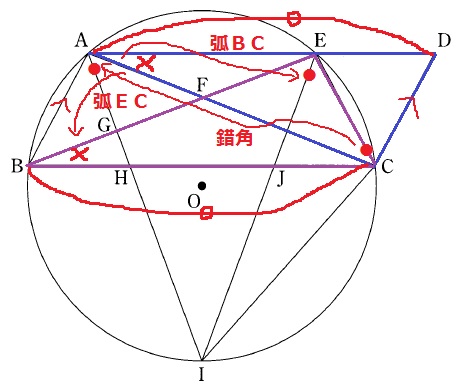
平行四辺形ABCDの対辺は等しい。AD=BC
弧ECに対する円周角(×)から、∠CAD=∠EBC
AB//DCの錯角+弧BCに対する円周角(●)で、∠ACD=∠CAB=∠BEC
△ADCと△BCEの残りの角は等しい。∠ADC=∠BCE
1辺と両端角が等しく、合同となる。
@別解@
∠ADC=∠BCEについてです。
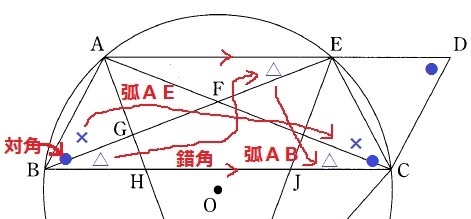
平行四辺形の対角は等しい。∠ADC=∠CBA(●)
これを∠ABE(×)と∠EBC(△)に分ける。
弧AEに対する円周角から、∠ACE=×
AE//BCの錯角と弧ABに対する円周角から、∠ACB=△
∠BCE=×+△=●となり、∠ADC=∠BCEが導ける。
(3)①
底辺は12cmなので、平行四辺形の高ささえわかればいい。
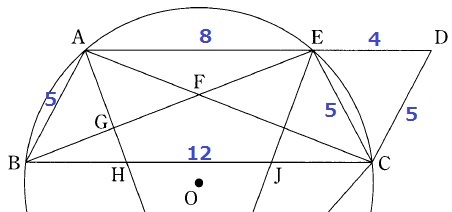
前問の合同から、EC=DC=5cm
△CDEは二等辺三角形。
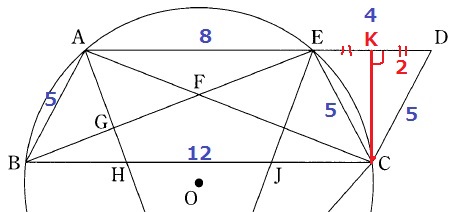
CからEDに向けて垂線、交点をKとする。
CKは二等辺三角形を真っ二つにする。
言い換えれば、CKを対称の軸として△CKEと△CKDは左右対称で合同。
KD=2cm
△CKDで三平方→CK=√21cm
平行四辺形ABCDの面積は、12×√21=12√21cm2
②
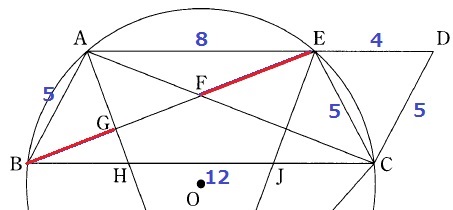
離れている。
AE//BC、AB=EC=5cm
また、(2)の合同図形から対角線AC=BEなので、
ここから四角形ABCEは等脚台形とわかる。
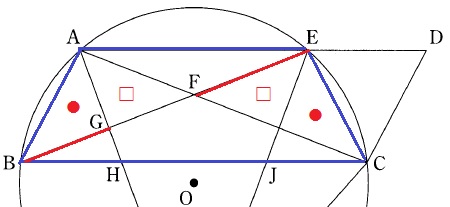
等脚台形は左右対称の図形。
BGを1辺とする△ABG(●)と、FEを1辺とする三角形(□)の形が違うような気がする。
結局、辺BE上でBG:GF:FEの連比処理をするしかないような…。
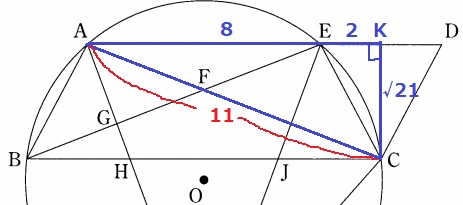
そこでBEの長さを求めたい。
等脚台形の対角線からBE=ACなので、前問の△ACKで三平方。
AC=11cm
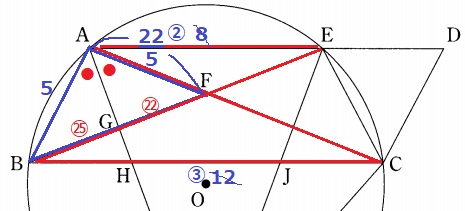
△AFE∽△CFBより、AF:FC=8:12=2:3
AF=11×2/5=22/5cm
ここで、角の二等分線の定理を用いる。
AB:AF=BG:GF
BG:GF=5:22/5=25:22
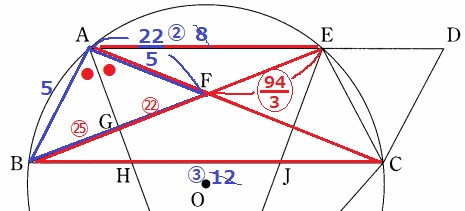
再度、△AFE∽CFBを使い、BF:FE=3:2だから、
FE=〇47×2/3=〇94/3
BG:FE=25:94/3=75:94
●講評●
平均は6割弱とやや高め。
大問1
基本問題ゆえ、全問とりたい。
大問2
(1)固定費と変動費をつかった数量変化。よくあるパターンなので慣れておきたい。
(3)確率も難しくはなかった。
大問3
グラフがスッキリしており、やりやすかった。
(3)①点座標の移動だけで正解できてしまう。
②面積を2等分する線分も見つけやすく、計算処理も負担の無い設問であった。
大問4
(1)正三角錐の頂点の足は、底面の重心にあたることは知っておきたい。
(2)四角形ABCDの左側に注目する必要があり、応用力が問われた。
大問5
証明は円周角定理&平行線→錯角で全て調べられる。
あとは1個ずつ丁寧に拾えるか。
(3)②
数字がやらしい(;´Д`)
去年の後期でも大問5(3)で角の二等分線の定理が出たので、
三重県民は覚えておいた方がいいと思う。。



コメント