全受検者平均点;標準問題選択者23.2点(前年比;-6.9点)
学校裁量問題選択者30.1点(前年比;-9.2点)
合格者平均点;標準問題選択者23.3点、学校裁量問題選択者30.9点


問題はこちら→東進ハイスクールさん(解答)
学校裁量問題(大問5)は21ページ以降です。
大問1(小問集合)
問1(1) 98.3%
-5×3
=-15
(2) 77.8%
9-62
=9-36
=-27
(3) 63.5%
√14×√7-√8
=√98-2√2
=7√2-2√2
=5√2
問2 50.2%
絶対値が4の数
→数直線上で原点0から距離が4の数。
-4、4
問3 57.1%
7つの中央値は(7+1)÷2=4番目の値。
25.9℃
問4 78.7%
ネジレの位置→延長しても交わらない、かつ平行でない。
辺OC
問5 71.6%
y=-6×(-3)/2=9
問6 52.3%
円周角の定理より、∠ACB=90°
△ABCで三平方→AC=√21cm
大問2(小問集合2)
問1 69.8%
3x(x+2y)+y(x+2y) ←共通因数(x+2y)でくくる
=(x+2y)(3x+y) ←代入
=(1-4)(3-2)
=-3×1=-3
問2 56.8%
マークの並びは、♠♦♠か♦♠♦のどちらか。
♠♦♠の場合、♠は(1、2)(2、1)の2通り。
♦は1or2の2通り。
2×2=4通り
♦♠♦も同様に4通り。
計8通り
問3 29.8%!
∠PBC=30°となる点Pの作成。
はじめは辺BCしか見ないほうがいい。

①BCを1辺とする正三角形をつくる。
②60°を角の二等分線で分割。30°の作成。
③ACとの交点がPとなる。
問4(1) 34.9%

式であらわしてみよう。
〔道旗の縦〕×5/7=道章の直径(a)
〔道旗の縦〕=a÷5/7=7/5acm
(2) 20.8%!
道旗の縦をxとすると、横は3/2x。
x×3/2x=9000 …方程式
3/2x2=9000
x2=6000
x>0より、x=√6000=10√60=20√15
20√15cm
大問3(整数)
問1 43.0%
初日である1日目の曜日が同一であれば、共通する1~30日の曜日が等しくなる。
9月1日と同じ曜日となるのは、9月1日から7の倍数後の日。
ア…7
9月1日~12月1日までの日数を数える。
『9月1日からn日後』なので、9月は30-1=29日間となる。
29+31+30+1=91日後
イ…91
*31日がない小の月→『西向く士小の月』
2(に)・4(し)・6(む)・9(く)・11(漢数字の十一→士)
91=7×13と表せるので、91は7の倍数。
→9月1日から91日後の12月1日は同じ曜日となる。
ウ…13
問2 8.9%!!
中学受験では日暦算という独立した単元があるが、高校受験では珍しい。
うるう年である2020年と『1年間のすべての日の曜日が同じになる年』だから、
求める年は自動的に、うるう年にしぼられる。
(平年には2月29日がなく、すべての日の曜日が同じにならない)
うるう年で、かつ2020年と同様に1月1日が水曜日になる年を探す。
資料でうるう年に着目すると、『水→月→土→木…』と5個ずつ曜日がズレている。
(うるう年は2個、平年は1個ずつ曜日がズレ、4年で5個ズレる)
曜日は7つで1周するので、5個ズレるということは2個前にズレるのと一緒。
『水→月→土→木→火→日→金→水!』
2020年の次に1月1日の曜日が水曜となるうるう年は、
4年×7=28年後の2048年。
同様に、その28年後も1月1日が水曜のうるう年→2076年
その次は2104年で2100年をオーバーする。
2048年と2076年
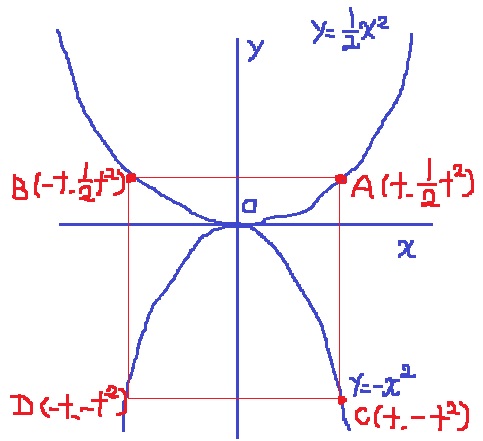
大問4(関数)
問2 43.2%
t=4をC座標に代入。
C(4、-16)
つづいて、y=ax+bに代入。
-16=-3×4+b
b=4
y=-3x+4
問3 11.2%!
傾き(変化の割合)=yの増加量/xの増加量
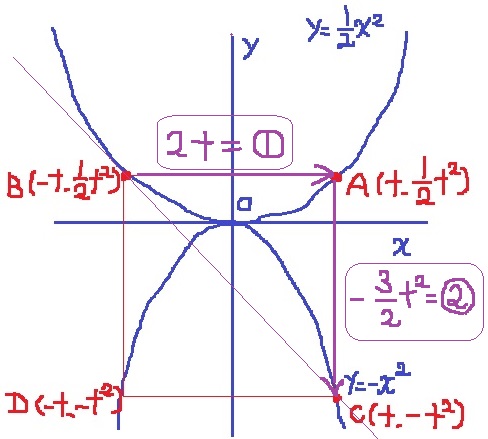
BCを通る直線の傾きが-2ということは、
xの増加量…B→A=2t …①
yの増加量…A→C=-3/2t2 …②で、
②=①×(-2)となる。
-3/2t2=2t×(-2)
-3t2=-8t
3t2-8t
=t(3t-8)=0
t>0より、t=8/3
y=1/2x2にx=8/3を代入する。
y=1/2×(8/3)2=32/9
A(8/3、32/9)
大問5(平面図形)
問1 60.5%
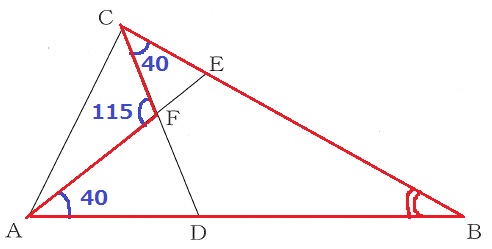
赤線でブーメラン型。
ブーメランの角の和は股の角(証明は外角定理を使います)
∠ABC=115-(40+40)=35°
問2 5.6%!!
△ABC∽△EBDの証明。
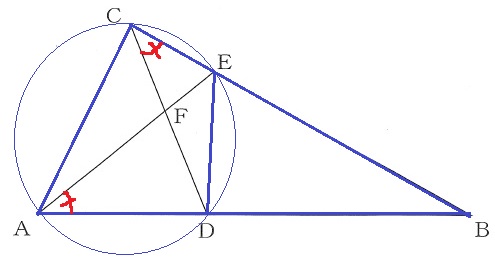
↑∠BAE=∠BCDから、この円が見えるようにしたい。
2点A、Cが直線DEについて同じ側にあって、∠DAE=∠DCEが成り立つから、
円周角定理の逆より、4点A、C、E、Dは同一円周上にある。

『円に内接する四角形の内角は、その対角の外角に等しい』
これと共通角を合わせ、2角相等→∽
学校裁量問題
問1(1) 90.4%
毎分60mで30分歩く。
60×30=1800m
(2) 12.6%!
復路も30分なので、全体の所要時間は80分。
これを変えずに、図書館での滞在時間を30分に伸ばす。
残りの50分が移動時間。
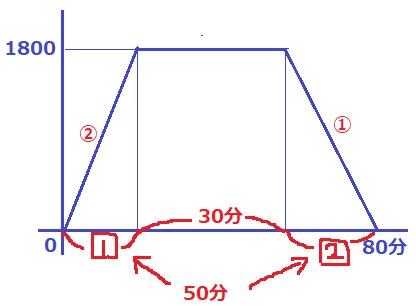
速さの比は、往路:復路=2:1
時間の比は速さの逆比。
時間の比は、往路:復路=1:2
往路の時間…50分×1/3=50/3分
往路の速さ…1800÷50/3=毎分108m
問2(1) 74.0%
(1×2+2×4+3×1+4×2+5×1+6×1+7×3+8×5+9×3+10×3)÷25
=6冊
(2) 22.0%!
ここも。。。(;´Д`)
25人の中央値(メジアン)は、(25+1)÷2=13番目の値
図2で、1~5冊までの度数の和は、4+3+1+1+2=11人
6冊は0人で、中央値の13番目は8冊でないといけないから、7冊は1人となる。
8冊と9冊の合計人数は、25-(11+1+4)=9人
平均値6冊なので、ここから8冊or9冊読んだ人の合計冊数を求める。
6×25-(1×4+2×3+3×1+4×1+5×2+7×1+10×4)
=76冊
8冊読んだ人をx人とすると、9冊読んだ人は9-x人。
8x+9(9-x)=76
x=5
まとめると、7冊が1人、8冊が5人、9冊が4人。
*採点基準によれば、7冊の度数が当たっていると2点もらえる。
問3(1) 53.9%
Dは半円の中心。
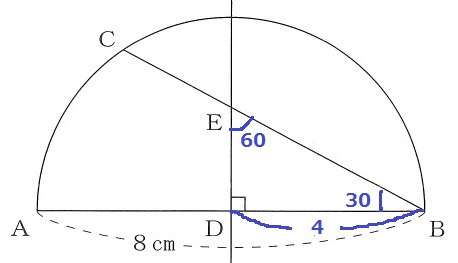
△EBDの内角が30°-60°-90°→辺の比が1:2:√3
DE=4×1/√3=4√3/3cm
(2) 12.1%!
記述式。

Cから垂線をおろし、ABとの交点をFとする。
半径より△CBDは二等辺。
CD=4cm、∠DCB=30°
△CBDで外角定理→∠CDF=30+30=60°
ここから△CDFの内角も30°-60°-90°で1:2:√3
CF=2√3cm
FD=2cm
回転体の体積は、円柱から高さの比でショートカットできる。
すなわち、FD:DB=2:4=1:2から、円柱の2/3倍が求積すべき体積。
2√3×2√3×π×6÷3×2/3=16πcm3
●講評●
大問1
問2;絶対値。半分しか正答していないだと!?
完全解答。±4でも正解。
大問2
問3;作図。∠ABCは無視すること。
問4;道旗を用いた特殊な設問だが、仕組みはシンプル。
(1)分母分子の逆に気を付けよう!
大問3
問2;カレンダー問題。中学入試に出てくる設問は正答率がガクッと下がる。
平年と閏年では何曜日がズレるか。そこから周期性を見出す。
大問5
問2;円に内接する四角形の性質は覚えておくと応用がきく。
(学校裁量)
問1(2)中学受験生はかなり正解してくる!
問2(2)処理が面倒で時間の確保が必要。
問3それほど難しくはない。時間をどれだけ残せたか。



コメント