2022年度　奈良県公立高校入試問題過去問【数学】解説

平均26.3点（前年比；－1.3点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）－71.6％

（１）①　99.0％
３－７
＝－４

②　92.7％
４（ｘ＋２）＋２（ｘ－３）
＝４ｘ＋８＋２ｘ－６
＝６ｘ＋２

③　93.3％
12ｘ²ｙ÷４ｘ²×３ｘｙ
＝９ｘｙ²

④　87.1％
（ｘ＋２）（ｘ＋８）－（ｘ＋４）（ｘ－４）
＝ｘ²＋10ｘ＋16－ｘ²＋16
＝10ｘ＋32

（２）　79.8％
ｘ²－６ｘ＋２＝０
解の公式を適用。ｘの係数が偶数なのでｂ＝２ｂ’が使える。
ｘ＝３±√７

（３）　81.3％
ｘ²－６ｘ＋９
＝（ｘ－３）²　←ここで代入
＝（√２＋３－３）²
＝２

（４）　77.6％
ｙ＝ａｘ²に（ｘ、ｙ）＝（２、－８）を代入。
－８＝４ａ
ａ＝－２
ｙ＝－２ｘ²
*誤答例：ｙ＝－４ｘ

（５）　82.1％
40人の中央値（メジアン）は20番目と21番目の平均。
20～25分の階級に含まれる。
相対度数は、６/40＝0.15

（６）　46.6％

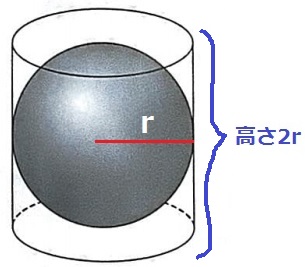
【球の体積：４/３πｒ³】
円柱の体積→底面の半径ｒ、高さ２ｒなので、πｒ²×２ｒ＝２πｒ³
球：円柱＝４/３πｒ³：２πｒ³＝２：３
球の体積は円柱の２/３倍。
*誤答例：３/２、２/３π

（７）　62.1％
Ｄに止まるには、出目の合計が３・７・11。
●和が３→（１、２）（２、１）
●和が７→（１、６）（２、５）（３、４）（４、３）（５、２）（６、１）
●和が11→（５、６）（６、５）
計10通り。
全体は６×６＝36通り
確率は、10/36＝５/18
*誤答例：５/36、１/18

（８）　43.1％
∠ＡＰＣ＝45°の作図→直角二等辺三角形を想像する。

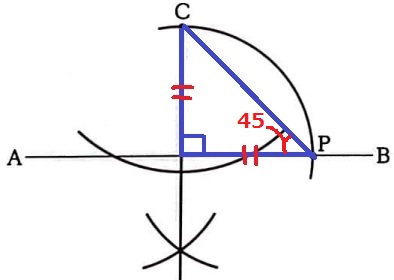
Ｃを通る垂線を作成。
その足からＣの長さをとり、ＡＢ上に移す。
直角二等辺の内角45°が∠ＣＰＡになる。
*誤答例：線分ＡＢ上にＣＡ＝ＣＰとなるように点Ｐをとる。

大問２（数量変化）－47.8％

（１）①　86.3％
50ｃｍは容器の高さ。水面の高さで等式を立てる。
１分間あたりａは12ｃｍ、ｂは６ｃｍだから12ａ＋６ｂ。

②　74.6％

Ａだけを使った場合が直線ℓ。
６分後に高さ50ｃｍとなるように設定して、Ｂだけを使った場合が直線ｍ。
交点がＡからＢに切り替えるタイミング。

い：直線の傾きは、１分あたりに高くなる水面の高さ
う：交点のｘ座標はＡの使用時間
ウ

（２）①　19.1％！

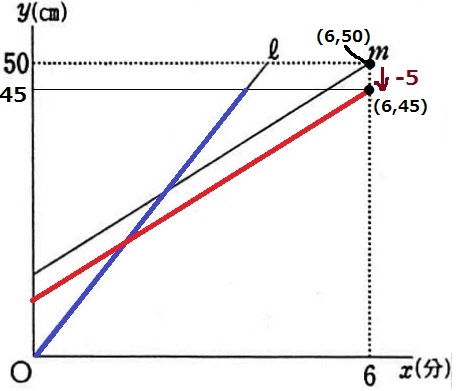
*ゴールを50ｃｍから45ｃｍに下げる。
直線ｍが（６、45）を通過するには、
『直線ｍをｙ軸方向に－５平行移動させた直線』を描けばいい。
*誤答例：直線ｍに平行な別の直線

②　67.5％

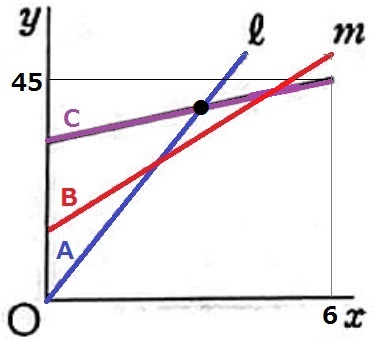
（６、45）をゴールとして傾き２の直線を描く。
交点がＡからＣにチェンジする時間。

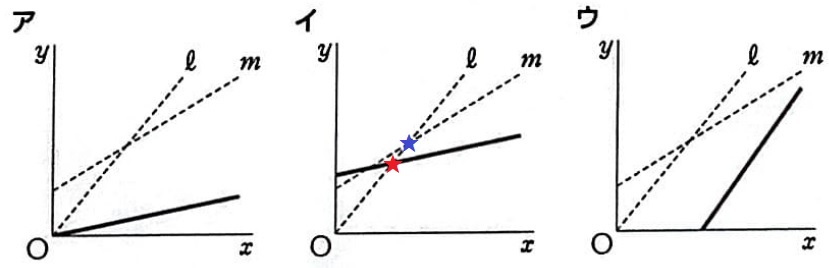
誤答のチェック。
Ｃの傾きは最も緩やかなのでウは×。
アのようにスタート（原点）を一緒にするのではなく、ゴールを先に設定する。
イは下げ過ぎ。『図２をもとに』考えるので、ℓ・ｍの最後はｙ＝50
時間がかかるのでやらなくても良いが、方程式を解くとｍとの交点はℓとの交点より上にくる。
エ

（３）　19.3％！

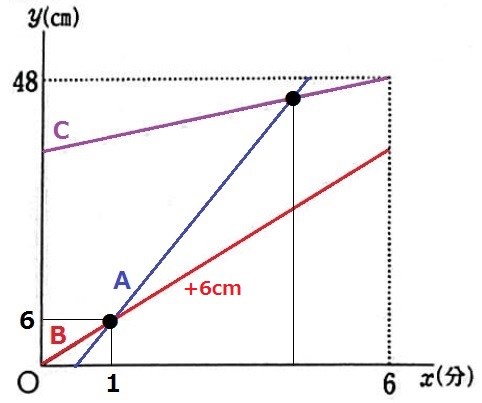
与えられたグラフにＡを描きこむ。
Ｂ⇒Ａは１分後にチェンジで、このときの水面の高さは６ｃｍ。
Ａは（１、６）を通過する。

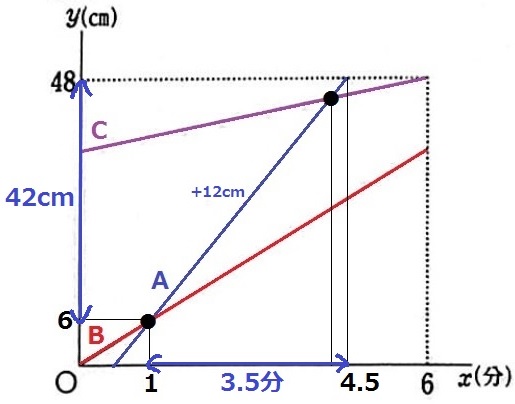
もし、このままＡだけだったら何分で終わるのか？
残り42ｃｍを毎分12ｃｍずつ埋めていくので、
42÷12＝７/２＝3.5分
Ｂを入れ始めてから4.5分後である。

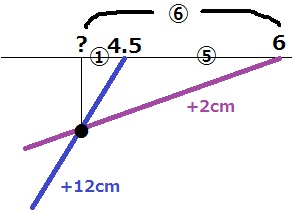
グラフの最後をピックアップ。
変化率はＡ：Ｃ＝12：２＝６：１
水面を同じ高さにするまでの時間は逆比で、Ａ：Ｃ＝①：⑥
Ａ⇒Ｃに切り替えた時間で残りの水面をＡは①の時間、Ｃは⑥の時間かかるので、
差の⑤が６－4.5＝1.5分にあたる。
①＝1.5×①/⑤＝0.3分＝18秒
答えは、4.5分（４分30秒）の18秒前の４分12秒後。
*誤答例：３分12秒後

大問３（関数）－46.0％

（１）　91.8％
ｙ＝６/ｘにｘ＝１を代入して、ｙ＝６

（２）　51.4％

二等辺三角形ＯＣＤを縦半分に割り、反対側にくっつけると長方形になる。
ｙ＝６/ｘより、ｘｙ＝６
→Ｃのｘ座標とｙ座標の積が６→長方形は常に６→二等辺三角形ＯＣＤの面積も６で一定。
オ
*誤答例：ウ

（３）　35.7％

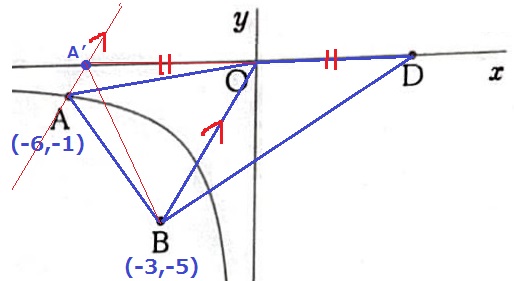
Ａを通るＢＯに平行な線をひき、ｘ軸との交点をＡ’とする。
△ＯＡ’Ｂと△ＯＢＤが等積なので、底辺はＡ’Ｏ＝ＯＤとなる。
Ａ’のｘ座標がわかればいい。

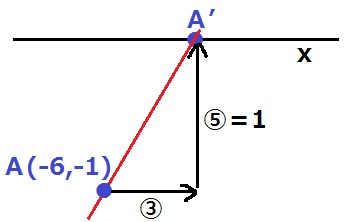
ＢＯの傾きは５/３。
Ａから右に③、上に⑤移動してＡ’
⑤＝１だから、③＝１×③/⑤＝３/５
Ａ’のｘ座標は、－６＋３/５＝－27/５
これをｙ軸について対称移動させたＤのｘ座標は27/５。
*誤答例：（27/５、０）、24/５

（４）　22.2％！

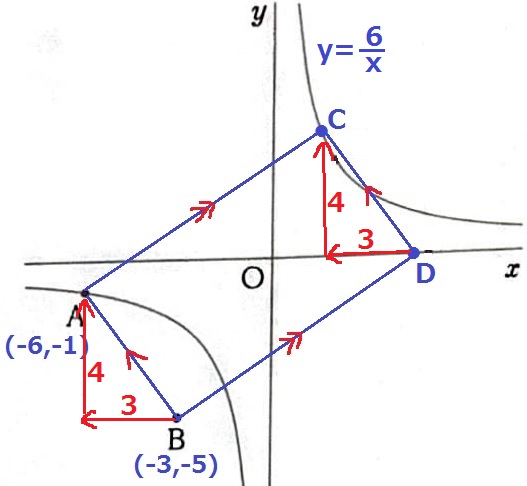
Ｂ（－３、－５）⇒Ａ（－６、－１）
左に３、上に４の移動はＤ⇒Ｃでも同じ。
Ｄのｙ座標は０なので、Ｃのｙ座標は４。
これをｙ＝６/ｘに代入して、Ｃのｘ座標は３/２。

Ａ（－６、－１）⇒Ｃ（３/２、４）
右に15/２、上に５移動だから、ＡＣの傾きは５÷15/２＝２/３
ＡＣ//ＢＤより、ＢＤの傾きも２/３。
Ｂから右に３、上に２移動して、切片は－５＋２＝－３
ｙ＝２/３ｘ－３
*誤答例：ｙ＝３/４ｘ－３

大問４（平面図形）－28.3％

（１）　54.4％

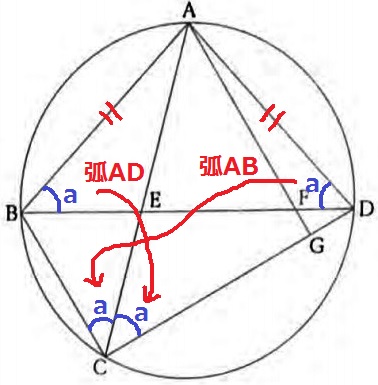
△ＡＢＤは二等辺三角形だから、∠ＡＤＢ＝ａ
弧ＡＤに対する円周角で、∠ＡＢＤ＝∠ＡＣＤ＝ａ
弧ＡＢに対する円周角で、∠ＡＤＢ＝∠ＡＣＢ＝ａ
∠ＢＣＤ＝２ａ°
*誤答例：180－ａ°、90－ａ°

（２）　65.6％
△ＡＥＦ∽△ＣＥＢの証明。

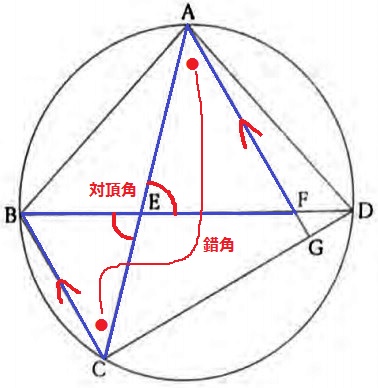
対頂角＋ＡＧ//ＢＣの錯角で２角相等→∽

（３）①　2.0％!!

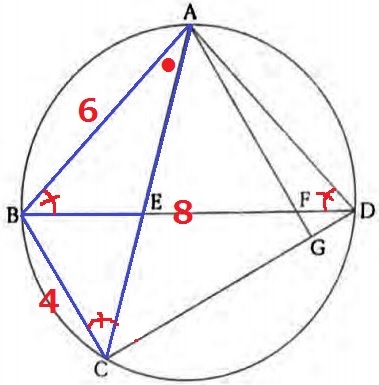
（１）がヒントになる。
∠ＡＢＥ＝∠ＡＣＢ、共通角で∠ＢＡＥ＝∠ＣＡＢ
２角が等しく、△ＡＢＥ∽△ＡＣＢ
相似比は、ＡＢ：ＡＣ＝３：４
面積比は相似比の２乗、△ＡＢＥ：△ＡＣＢ＝⑨：⑯
△ＢＣＥの面積は、⑯－⑨＝⑦
△ＡＢＥの面積は△ＢＣＥの９/７倍。
*誤答例：３/２、９/４

②　0.0％!!!
シビアです:(っ`ω´c):

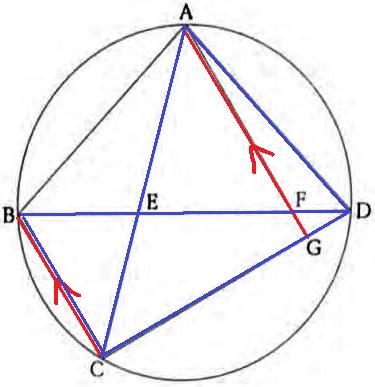
角度の数値が与えられていないので、有名角は使えない。
かといって、Ｇが変な位置にあるのでＡＧを１辺とする三角形の相似も見当たらず…。
本問の図形で特徴的なのはＡＧ//ＢＣ
知りたいのはＡＧの長さ。ＢＣは４ｃｍとわかっている。
ＡＧ：ＢＣの比を何かに置き換えることはできないか。

ここで、△ＡＣＤと△ＢＣＤに着目する。
２つの三角形はＣＤが共通の底辺。
高さは底辺に対して垂直であるが、高さの比は斜めでも許される。
２本の斜線が平行であれば底辺に対する角度が等しいので、高さの比が利用できる。
すなわち、△ＡＣＤ：△ＢＣＤの面積比がＡＧ：ＢＣである。

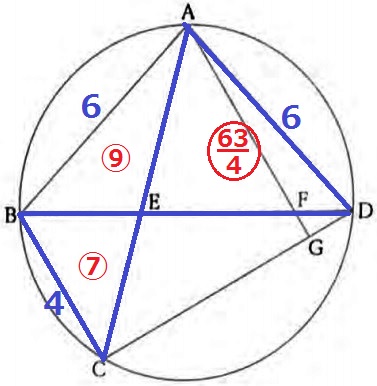
前問の解答を用いる。
△ＡＢＥ＝⑨、△ＢＣＥ＝⑦として、△ＡＤＥと△ＣＤＥの面積比を算出する。
△ＡＤＥ∽△ＢＣＥで相似比３：２⇒面積比は９：４
△ＡＤＥの面積は、⑦×９/４＝〇63/４

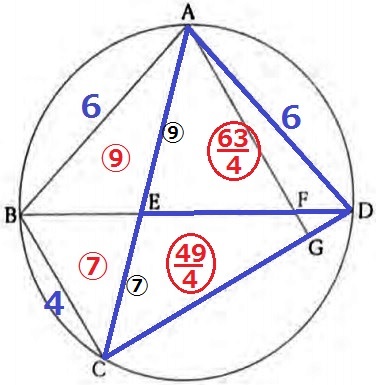
△ＡＢＥ：△ＢＣＥ＝ＡＥ：ＥＣ＝△ＡＤＥ：△ＣＤＥ＝９：７
△ＣＤＥの面積は、〇63/４×７/９＝〇49/４

△ＡＣＤ…〇63/４＋〇49/４＝〇112/４
△ＢＣＤ…⑦＋〇49/４＝〇77/４
△ＡＣＤ：△ＢＣＤ＝112/４：77/４＝16：11
したがって、ＡＧの長さは、４×16/11＝64/11cm
*誤答例：４√２、６、７