2025年度　埼玉県公立高校入試問題（学校選択）過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
（２ｘ－ｙ）/３－（３ｘ－２ｙ）/４
＝｛４（２ｘ－ｙ）－３（３ｘ－２ｙ）｝/12
＝（８ｘ－４ｙ－９ｘ＋６ｙ）/12
＝（－ｘ＋２ｙ）/12

（２）
３ｘｙ＋６ｘ－ｙ－２　←３・６のところがくくれそう
＝３ｘ（ｙ＋２）－（ｙ＋２）
＝（３ｘ－１）（ｙ＋２）　←代入
＝｛３（√６＋２）－１｝（√６－２＋２）
＝√６（３√６＋５）
＝18＋５√６

（３）
４ｘ（ｘ－３）＝（ｘ－３）²　←（ｘ－３）＝Ａとおく
４ｘＡ＝Ａ²
Ａ²－４ｘＡ
＝Ａ（Ａ－４ｘ）　←（ｘ－３）に戻す
＝（ｘ－３）（ｘ－３－４ｘ）
＝（ｘ－３）（－３ｘ－３）　←後半を－３でくくる
＝－３（ｘ－３）（ｘ＋１）
ｘ＝３、－１

（４）
*共通問題（11）

ア：21人の中央値は（21＋１）÷２＝11番目の値で66。〇
イ：第１四分位数は下位10人の真ん中、下から５番目と６番目の平均で54。〇
ウ：第３四分位数は上位10人の真ん中、上から５番目と６番目の平均で76。×
エ：範囲＝最大値－最小値＝90－45＝45。〇
ウ

（５）
*共通問題（15）
連続する２つの自然数をｎ、ｎ＋１とする。
ｎ²＋（ｎ＋１）²
＝２ｎ²＋２ｎ＋１＝365
２ｎ²＋２ｎ－364＝０　←÷２
ｎ²＋ｎ－182
＝（ｎ－13）（ｎ＋14）＝０
ｎ＞０より、ｎ＝13
連続する２つの自然数は13と14
13と14

（６）
反比例の比例定数ａ＝ｘｙ＝18
（１、18）（２、９）（３、６）（６、３）（９、２）（18、１）
反比例は双曲線。これらの負の座標を含めて12個。

（７）
2023年都立大問５（２）で類題がでている。
まずは１辺６ｃｍの正四面体の体積を求める。

Ａからおろした垂線の足であるＨは正三角形ＡＢＣの重心であり、中線を２：１に内分する。
ＡH＝２√３ｃｍ
△ＯＡＨで三平方→高さＯＨ＝２√６ｃｍ
正四面体の体積は、６×３√３÷２×２√６÷３＝18√２ｃｍ³

高さ一定→底面積の比＝体積比だから、
三角錐Ａ―ＯＰＱ：三角錐Ｏ―ＰＢＣＱ＝△ＯＰＱ：四角形ＰＢＣＱ＝①：③
求積すべき立体の体積は、18√２×③/④＝27√２/２ｃｍ³

＠余談＠
一発で正四面体の体積を出す公式がある。

１辺ａの正四面体の体積…Ｖ＝√２/12ａ³

１辺６ｃｍだと、Ｖ＝√２/12×６³＝18√２
これを知っているか否かで時間短縮が半端ない。。
理由は１辺をａとして地道に三平方で導きます。

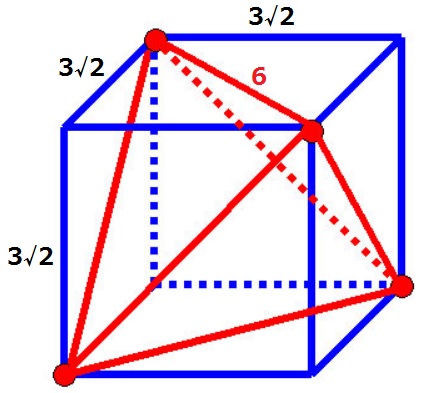
数学切り抜き帳より。また、正四面体はこのように立方体に収納することができる。
正四面体の１辺は正方形の対角線。１：１：√２から立方体の１辺は３√２ｃｍ
立方体から４つの三角錐をひけば、真ん中の正四面体になる。
三角錐の底面積は正方形の１/２倍。錐の体積は柱の１/３倍。
立方体の体積を⑥とすると、１つの三角錐の体積は⑥×１/２×１/３＝①
正四面体の体積は、⑥－①×４＝②
（３√２）³×②/⑥＝18√２ｃｍ²

（８）

通分して式をいじりたくなるが、百分率でそのまま計算するのが良いと思う。
【２/３～１→66.6％～100％】
いずれかに１を入れると100％を超えるので不適。
範囲内に収まるのは、１/２＋１/３、１/２＋１/４、１/２＋１/５
（ｘ、ｙ）＝（２、３）（２、４）（２、５）とこれらの逆を含めた６通りである。
全体は５×４＝20通りだから、確率は６/20＝３/10

（９）

弧ＢＣに付き合わなければならないので、
方針としては〔扇形ＯＢＣ－四角形ＯＢＥＣ〕を目指す。
錯角と対頂角から直角二等辺がいろいろでてくる。
水色の直角二等辺より、ＯＦ＝４×１/√２＝２√２ｃｍ
ＦＣ＝４－２√２ｃｍ
緑色の直角二等辺でＤＯ＝２√２ｃｍ、ＢＤ＝４－２√２ｃｍ
１辺両端角相当で、△ＢＤＥ≡△ＣＦＥ

ＯＥに補助線。
３辺相等で△ＢＯＥ≡△ＣＯＥ（ＯＥを対称の軸として左右対称）
ＥＤ＝ＥＦ＝４－２√２ｃｍ
求積すべき図形の面積は、４×４×π×１/８－４×（４－２√２）÷２×２
＝２π＋８√２－16ｃｍ²

（10）
共通問題（16）
Ｂ中の54～56回の相対度数は、21/60＝７/20＝35/100＝0.35
ア…0.35
＠＠
54回以上とんだ生徒の割合が大きい→54回以上の階級の相対度数の合計が大きい。
Ａ中…0.25＋0.35＋0.20＝0.8
Ｂ中…0.35＋0.15＋0.05＝0.55
Ａ中の方が54回以上とんだ生徒の割合が大きい。

大問２（平面図形）

（１）

円Ｏは△ＰＱＲに内接する→円外の点からひいた接線上にＱ・Ｒがある。
接線と半径は接点で直交＋半円の弧に対する円周角は直角
⇒直径をＰＱとする円を描き、円Ｏとの交点が接点になる。

また、ＰＱ＝ＰＲから△ＰＱＲは二等辺三角形。
直線ＰＯを対称の軸としてＱとＲは対応する点で、対称的な位置関係にあるからＰＯ⊥ＱＲ
ＱＲは円ＯとＰの反対側で接する。

①ＰＯの垂直二等分線とＰＯとの交点を中心として円を描く。
②接点に向かって２本の接線をひく。
③円Ｏの右側の点を通るＰＯの垂線をひく。
④反時計回りにＰ→Ｑ→Ｒだから、下がＱ、上がＲ。

（２）
四角形ＤＥＦＡの対角線ＤＦとＡＥがそれぞれの中点で交わることの証明。

『それぞれの中点で交わる』の言い回しから平行四辺形の性質を想起したい。
四角形ＤＥＦＡが平行四辺形であることを示せばいい。

ＢＤ＝②、ＤＡ＝①
ＥとＦが中点であることに着目する。
△ＢＣＤにおいて中点連結定理より、ＥＦ//ＢＤ、ＥＦ＝①
ＥＦ//ＤＡ、ＥＦ＝ＤＡ
１組の対辺が平行かつ長さが等しいから、四角形ＤＥＦＡは平行四辺形である。
したがって、ＤＦとＡＥは平行四辺形ＤＥＦＡの対角線だから、それぞれの中点で交わる。

大問３（規則）

共通問題と同様。
（１）

最大値【２、３、５、８…】
２＋３＝５
３＋５＝８
前の２項の和が連なるフィボナッチ数列である。
５＋８＝13（図から確認してもいい）
＠＠
値の合計【３、９、27、81…】
３の累乗るいじょうが連なる。81×３＝243
ア…13、イ…243

＠余談＠
なぜ値の合計は３倍になるのか？

自身の分身が両サイドに移動して他の分身と合体する。
もとの２倍増えるから、すべての値を合わせると３倍になる。

（２）
ａとｂの和の９倍→９（ａ＋ｂ）を目指す。

すべての点をａ、ｂで表す。
ａ＋ｂ＋２（ａ＋ｂ）＋２（２ａ＋ｂ）＋２（ａ＋２ｂ）
＝９（ａ＋ｂ）

（３）
前問の結果は、操作２回目で点の値の合計が最初の和ａ＋ｂの９倍（＝３²）だった。
今度は最初の和が２＋５＝７だから、操作ｎ回目は７×３^ｎ＝1701
３^ｎ＝243
ｎ＝５
最大値はフィボナッチをしていく。
２回目‥５＋７＝12、３回目‥７＋12＝19
４回目‥12＋19＝31、５回目‥19＋31＝50
ｎ…５、最大値…50

大問４（関数）

（１）
共通問題と同様。
ｙ＝３/４ｘ²にｘ＝－２、４を代入して、ＡとＢの座標を求める。
Ａ（－２、３）→Ｂ（４、12）
右に６、上に９だから、傾きは９/６＝３/２
Ａから右に２、上に３移動して、切片は３＋３＝６
ｙ＝３/２ｘ＋６

（２）

ＡＯ；ｙ＝－３/２ｘ
ＢＣの傾きも－３/２
Ｂから右に②、下に③進んでＣ。③＝12だから、②＝８
Ｃ（12、０）

回転体は底面の半径３ｃｍ、高さ12ｃｍの円錐である。
体積は、３×３×π×12÷３＝36πｃｍ³

（３）

求めたいＰのｘ座標をｔとする。Ｐ（ｔ、３/４ｔ²）
以下、面積の÷２を省略。
△ＢＤＰの面積…12（４－ｔ）＝－12ｔ＋48

Ｐを通るＯＡに平行な線をひき、ｙ軸との交点をＰ’とする。
等積変形で△ＯＡＰ＝△ＯＡＰ’
ＡＯの傾きは－３/２
Ｐから左に②＝ｔ、上に③移動するから、Ｐ’のｙ座標は３/４ｔ²＋３/２ｔ
△ＯＡＰ’の面積…２（３/４ｔ²＋３/２ｔ）＝３/２ｔ²＋３ｔ

２つの三角形が等積なので、
３/２ｔ²＋３ｔ＝－12ｔ＋48
３ｔ²＋30ｔ－96＝０　←÷３
ｔ²＋10ｔ－32＝０
解の公式を適用。ｔの係数が偶数なので、ｂ＝２ｂ’が使える。
０＜ｔ＜４より、ｔ＝－５＋√57
ｘ＝－５＋√57

大問５（空間図形）

（１）

ＡＦがわかれば、四角形ＡＢＥＦの面積が求まる。
正方形ＡＢＣＤ→ＡＤ＝15ｃｍ
半円の弧に対する円周角は直角→∠ＤＡＦ＝90°より、円の直径はＤＦ
ＡＤ：ＦＤ＝15：18＝⑤：⑥
△ＡＤＦの辺の比で三平方→ＡＦ＝〇√11＝15×〇√11/⑤＝３√11ｃｍ
四角形ＡＢＥＦの面積は、３√11×15＝45√11ｃｍ³

（２）
Ｏの半径の最大値→２つの球が広めにギシギシと詰まっている状況。

小円と大円が接する点を通る断面で切り取る。
求めたい小円の半径をｒとする。
縦15－３ｒ、横18－３ｒ、斜辺３ｒの直角三角形で三平方。
(*球同士の接点で２つの半径は一直線になる)

（15－３ｒ）²＋（18－３ｒ）²＝（３ｒ）²
｛３（５－ｒ）｝²＋｛３（６－ｒ）｝²＝９ｒ²
９（５－ｒ）²＋９（６－ｒ）²＝９ｒ²　←÷９
（５－ｒ）²＋（６－ｒ）²＝ｒ²
25－10ｒ＋ｒ²＋36－12ｒ＋ｒ²＝ｒ²
ｒ²－22ｒ＋61＝０
ｂ＝２ｂ’の解の公式より、ｒ＝11±２√15
横（円の直径）18ｃｍより縦（円柱の高さ）15ｃｍの方が短い。
少なくとも垂直方向の和から３ｒ＜15、ｒ＜５がいえるので、ｒ＝11－２√15
11－２√15ｃｍ

公立高校入試解説（目次ページ）に戻る