平均54点(前年比;+6点)

問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1) 89%
6-4×(-2)
=6+8
=14
(2) 87%
3(-x+y)-(2x-y)
=-3x+3y-2x+y
=-5x+4y
(3) 58%
x2+2xy+y2
=(x+y)2 ←代入
=(5+√3+5-√3)2
=102=100
(4) 62%
積が5→5×(1~6)の6通り。逆の並びで(1~6)×5も6通り。
しかし、(5、5)だけは逆にしても同じで重複する。
6×2-1=11通り
全体は6×6=36通りだから、確率は11/36
(5) 85%
5x+2y=4 …①
3x-y=9 …②
①+②×2をすると、11x=22
x=2
②に代入して、y=-3
x=2、y=-3
(6) 24%!

高さは、√(62-32)=3√3cm
6×6×3√3÷3=36√3cm3
大問2(方程式)
(1) 54%
a=-1を代入すると、
x2-x-8=0
解の公式を適用して、
x=(1±√33)/2
(2)ア 78%
x=1を代入。
1+a-8=0
a=7
イ 58%
今度はa=7を代入。
x2+7x-8
=(x-1)(x+8)=0
他の解は-8
大問3(データの活用)
(1) 94%
マス目を数える。
20人
(2) 59%
(0×4+1×5+2×5+3×2+4×3+5×1)÷20
=38÷20=1.9回
(3) 18%!
21人の中央値(メジアン)は11番目の値。
10番目と11番目がいずれも2回だったので、花子の記録を加えても中央値は2回。
平均値が1.9回⇒2.0回になる。
花子を含めた21人の総和は、2.0×21=42回
花子の回数は、42-38=4回
大問4(数量変化)
(1)ア…82%、イ…51%

4秒後と6秒後の様子を図示する。
8×4÷2=16
4×4÷2=8
ア…16、イ…8
(2)ア 56%
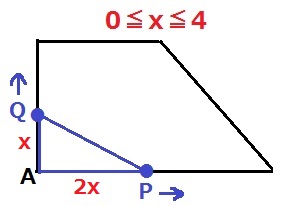
0≦x≦4はPがBを折り返す前で、QはAD上にある。
△APQの底辺は2x、高さはxだから、y=2x×x÷2=x2
y=x2
イ 36%
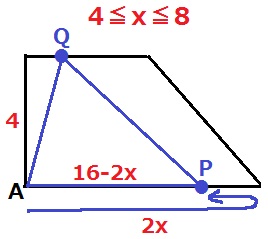
4≦x≦8はPがBを折り返し、QはDC上にある。
底辺はAB間の往復16cmからPの移動距離2xをひいて16-2x。
高さは4cmなので、y=(16-2x)×4÷2=-4x+32
y=-4x+32
(3) 47%
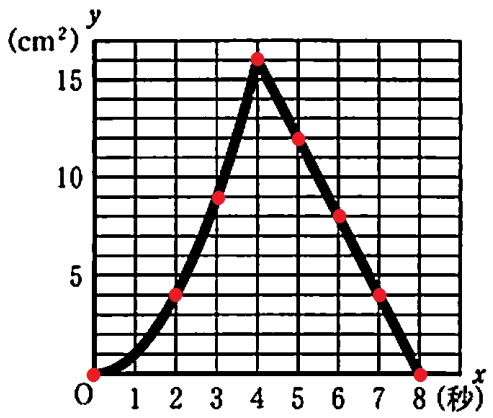
前問の式をグラフ化する。
通過すべき格子点を意識して描こう。
(4) 23%!
台形ABCDの面積は、(4+8)×4÷2=24cm2
△APQの面積は、24×3/8=9cm2
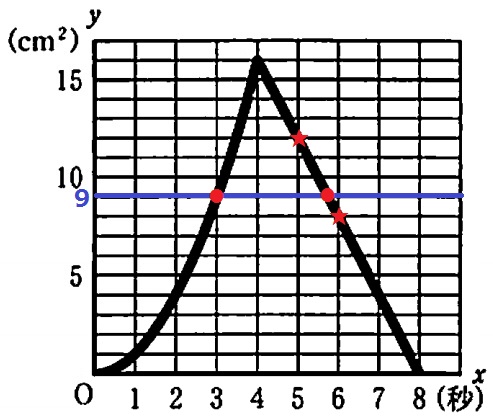
y=9となるxの値が答えになる。
前問の式を用いる。
y=x2とy=-4x+32にy=9を代入して、x=3、5.75
3秒後、5.75秒後
@余談@
後半は傾き-4だから1cm2下がるのに0.25秒かかるので、6-0.25=5.75秒
大問5(平面図形)
(1) 51%
△ABD∽△CBEの証明。
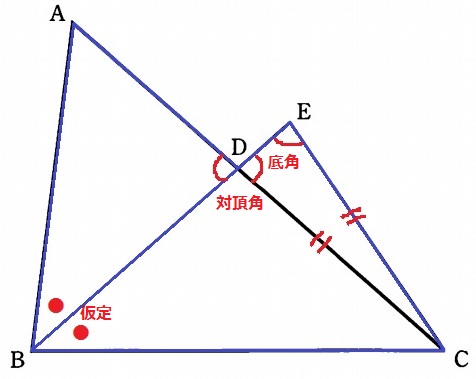
仮定の角の二等分線。対頂角と二等辺の底角。
2角が等しいので∽
(2)ア 31%!

前問の相似を利用する。
求めたいCEをxcmとする。
二等辺でCD=xcm、AD=6-xcm
【AB:AD=CB:CE】
4:(6-x)=5:x
内項と外項の積で、5(6-x)=4x
x=10/3
CEは10/3cm
イ 8%!!
相似比を器用に扱う。

△CDEは二等辺。DC=EC=10/3cm
AD=6-10/3=8/3cm
AD:DC=8/3:10/3=④:⑤
対応する辺の比でBD:BE=④:⑤だから、DE=⑤-④=①
隣辺比で面積比を算出する。
△ABD=④×④=16
△CDE=⑤×①=5
△ABDの面積は△CDEの16/5倍
大問6(規則)
(1)ア 80%
5回目は縦・横に数字が5つ並ぶ→25個
4回目は縦・横に4つ並ぶ→16個
新たに追加された数は、25-16=9個
イ 86%

書いて調べても良い。
計算では25から5ではなく4を引く点に注意!
21
@余談@
対角線上の数字は、【1・3・7・13・21…】
+2、+4、+6、+8となっている。
(2)ア…73%、イ…51%、ウ…47%、エ…36%
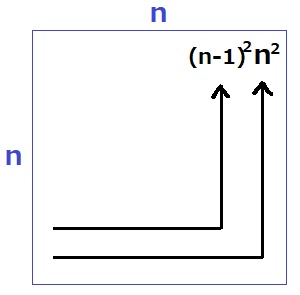
n回目の最大数は左上のn2
(n-1)回目の最大数はその左にある(n-1)2
n回目で新たに追加された数は、n2-(n-1)2=2n-1個
右下の数字は(1)イのとおり、n2からn-1をひく。
n2-(n-1)=n2-n+1
ア…n2、イ…(n-1)2、ウ…2n-1、エ…n2-n+1
(3)ア 62%
先ほどの式にn=10を代入。
102-10+1=91
イ 21%!
10回目の作業で追加された数は82~100の19個。
等差数列の和の公式より、(82+100)×19÷2=1729
●講評●
素直な問いが多い。
大問1
配点20点。
(4)計算で出せるが、樹形図で確実に調べても良い。
(6)立面図は1辺6cmの正三角形。
大問2
基本レベル。
大問3
ここもとりやすい。
(3)10・11番目がともに2回⇒花子を含んでも中央値は2回のまま。
大問4
タイピカルで他県でも見かける。
(2)底辺×高さ÷2をxを用いて行う。
(3)格子点をズラさないように!
大問5
(2)ア:ここらへんから差がつきやすい。
対応する辺がごちゃごちゃになったら、2つの三角形を脇に書いて整理する。
イ:図はシンプルだが、相似比の扱いに慣れていないと厳しい。
AD:DCは出しやすい。BD:DEは対応する辺の比から算出する。
大問5
(1)イ:25-5=20としないように!小さな数で実験してみる。
(2)難しくはないので、上位校狙いは完走したい。
(3)ア:等差数列の和の公式は知っておきたい。



コメント