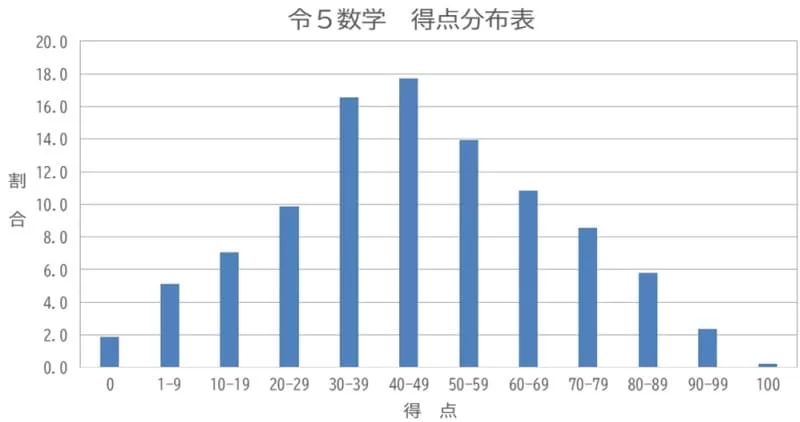
平均45.7点（前年比；＋3.4点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１） 91.5％
13＋３×（－２）
＝13－６
＝７
（２） 82.7％
１/３ａ－５/４ａ
＝－11/12ａ
（３） 58.5％
３ｘ＋７ｙ＝21
３ｘ＝－７ｙ＋21
ｘ＝（－７ｙ＋21）/３
（４） 72.6％
２ｘ＋ｙ＝５ｘ＋３ｙ＝－１
２ｘ＋ｙ＝－１ …①
５ｘ＋３ｙ＝－１ …②
①×３－②で、ｘ＝－２
①に代入、２×（－２）＋ｙ＝－１
ｙ＝３
ｘ＝－２、ｙ＝３
（５） 78.1％
９/√３－√12
＝３√３－２√２
＝√３
（６） 75.4％
ｘ2－２ｘ－24
＝（ｘ＋４）（ｘ－６）
（７） 44.2％
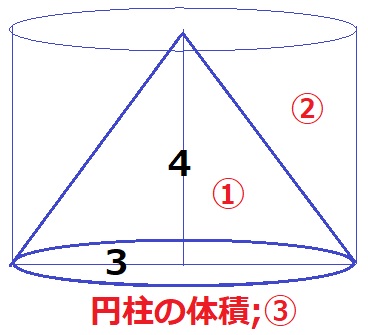
円柱の体積を③とすると円錐は①、求積すべき残りの部分は②。
３×３×π×４×②/③＝24π
（８） 55.3％
12人の第３四分位数は、上位６人のうち３番目と４番目の平均。
８と10の平均⇒９冊
（９） 66.0％
３枚の硬貨の結果は、２3＝８通り
●すべて裏：１通り
●２枚が裏：３枚のうち２枚の裏を選ぶ→表となる１枚を選ぶ→３通り
裏が２枚以上は計４通り、確率は４/８＝１/２
大問２（図形）
（１） 19.7％！
まずは10ｃｍから10√２ｃｍをつくる。
辺の比が１：√２といえば直角二等辺三角形。
10ｃｍの右端をＥ、左端をＨとする。
①Ｈを通るＨＥの垂線を作図。
②ＨＥの長さを垂線に移すと交点がＤ。
△ＤＨＥは直角二等辺で、ＤＥ＝10√２ｃｍ
③ＤＥを１辺とする正三角形を描き、交点がＦとなる。
（２） 16.0％！
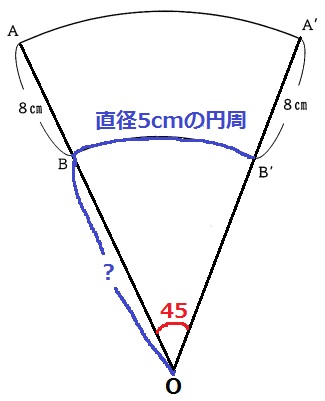
弧ＡＡ’を求めるには直径が必要だが、ＢＯが不明。
そこで、弧ＢＢ’の長さに着目する。
弧ＢＢ’は直径５ｃｍの円周の長さ。
円周と弧の長さが等しい場合、直径と中心角の関係は反比例である。
中心角の比は、円：弧＝360：45＝８：１
直径の比は逆比で、５：弧ＢＢ’の円の直径＝１：８
弧ＢＢ’の円の直径＝５×８＝40ｃｍ
弧ＡＡ’の円の直径＝40＋８×２＝56ｃｍ
弧ＡＡ’の長さは、56×π÷８＝７πｃｍ
（３）過程―12.9％！、解答―28.5％！
答案では求める過程も記述する。
斜線部が８×12＝96ｃｍ2
これが長方形の紙の面積の半分だから、周りの赤い部分も96ｃｍ2。
ｘ2×４＋２×（８＋12）×ｘ＝96
４ｘ2＋40ｘ－96＝０ ←÷４
ｘ2＋10ｘ－24
＝（ｘ＋12）（ｘ－２）＝０
ｘ＞０より、ｘ＝２
２ｃｍ
（４） 34.8％
組み立てると角錐台になる。
ネジレ→延長しても交わらない、かつ平行でもない。
ＡＢとねじれの位置にある辺は、辺ＤＩ、ＤＧ、ＤＣ（ＤＥ）
大問３（関数）
（１） 48.5％
ｙ＝ａｘ2において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）。
－１×（１＋３）＝－４
（２）解答―69.5％、グラフ―56.3％
ｙ＝ａｘ2に（２、２）を代入。
２＝４ａ
ａ＝１/２
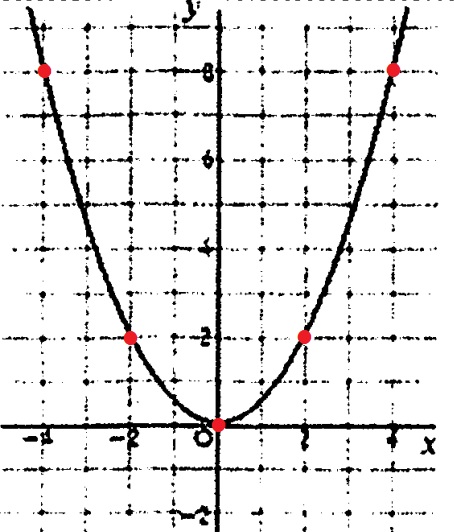
ｙ＝１/２ｘ2のグラフを描く。
通過すべき格子点は（－４、８）（－２、２）、原点、（２、２）（４、８）
（３） 15.9％！
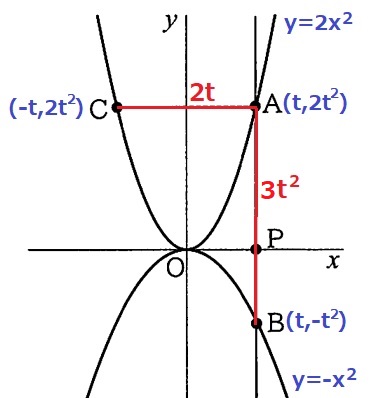
各座標をｔで表す。
Ａ（ｔ、２ｔ2）Ｂ（ｔ、－ｔ2）Ｃ（－ｔ、２ｔ2）
ＡＢ＝２ｔ2－（－ｔ2）＝３ｔ2
ＡＣ＝ｔ－（－ｔ）＝２ｔ
３ｔ2＋２ｔ＝１
３ｔ2＋２ｔ－１＝０
解の公式を使うと、ｔ＝（－１±２）/３
ｔ＞０より、ｔ＝１/３
（４）ｂ…5.1％!!、ｃ…5.1％!!
ｙ＝２ｘ2において、
ｘ＝０のとき、最小値ｙ＝０
ｘ＝３のとき、最大値ｙ＝18
ｙ＝ｂｘ＋ｃ（ｂ＜０）のｙの変域が０≦ｙ≦18になればいい。
傾きが負だから、ｘ＝－１のとき、最大値ｙ＝18
ｘ＝３のとき、最小値ｙ＝０
（－１、18）→（３、０）
右に４、下に18なので、傾きｂ＝－18/４＝－９/２
切片ｃは①：③に内分する点だから、ｃ＝18×③/④＝27/２
ｂ＝－９/２、ｃ＝27/２
大問４（平面図形）
（１） 2.1％!!
ＢＡ：ＢＣ＝ＡＤ：ＤＣ（角の二等分線の定理の証明）
ＤＢ//ＣＥの錯角と同位角で等角を移すと、△ＢＣＥは底角が等しい二等辺三角形。
ＢＥ＝ＢＣ …①
△ＡＣＥで平行線と線分の比からＡＢ：ＢＥ＝ＡＤ：ＤＣ …②
①、②より、ＢＡ：ＢＣ＝ＡＤ：ＤＣ
（２）① 25.7％！
ＡＢ：ＡＣ＝２：１→△ＡＢＣは辺の比が１：２：√３の直角三角形。
２角相等の相似から、△ＮＢＭも同様である。
ＮＢ＝②、ＭＢ＝〇√３とすると、ＡＢ＝〇２√３
面積比は相似比の２乗。
△ＡＢＣ：△ＮＢＭ＝（〇2√３）2：②2＝３：１
② 13.8％！
図形全体から取り去る図形を引くと、△ＡＢＣ≡△ＡＢ’Ｃ’だから、
求積すべき斜線部は大きい４分の１円から小さい４分の１辺を引けばいい。
10×10×π×１/４－５×５×π×１/４
＝（100－25）π×１/４
＝75/４πｃｍ2
クセの強い滋賀だが、今年はやりやすかった。
大問１
ここだけで配点が36点もある。
（７）柱から錘をくりぬいたら柱の２/３倍。
（９）３枚の硬貨を区別して考える。
大問２
（１）10：10√２＝１：√２から直角三角形を想像する。
（２）過去問にもコップ問題あったような・・。
中心角と直径（半径）の比の関係は知っておきたい。
（３）公式のように全体の長方形と斜線部で方程式でもＯＫ。
（４）角錘台と見抜きやすい。
大問３
取りやすい。
（３）求めたいＰのｘ座標ｔで各座標を表し、方程式を立てる。よくある典型題。
（４）先にｙ変域を出しておく。計算も複雑ではない。
大問４
（１）角の二等分線の定理は高校で習うが、余力があれば知っておきたい。
（２）①難しくないのが逆に怖い( ﾟAﾟ)
②軌跡の問題は高校受験では少ないが、中学受験では定番の構図である。
全体－白い部分＝斜線部分で、全体と白い部分をどう切り分けるか。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント