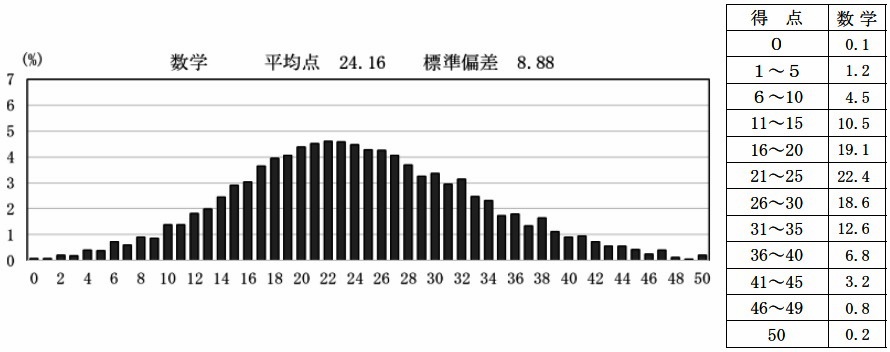
平均24.16点(前年比;-1.99点)
問題はこちら→東進ハイスクールさん(解答)
大問1(計算)
(1)ア 96.6%
9+3×(-6)
=9-18
=-9
イ 96.1%
(21ab-49b2)÷7b ←分配法則
=21ab÷7b-49b2÷7b
=3a-7b
ウ 94.3%
(x-y)/3-(x+2y)/5
={5(x-y)-3(x+2y)}/15
=(5x-5y-3x-6y)/15
=(2x-11y)/15
エ 81.2%
√6(8+√42)+√63 ←√6×√42=√6×√6×√7=6√7
=8√6+6√7+3√7
=8√6+9√7
(2) 77.3%
(2a-3)2-4a(a-5)
=4a2-12a+9-4a2+20a
=8a+9 ←ここで代入
=8×3/8+9
=12
(3) 86.6%
(x-8)(x-1)=x-13
x2-9x+8=x-13
x2-10x+21
=(x-3)(x-7)=0
x=3、7
大問2(小問集合)
(1) 74.2%
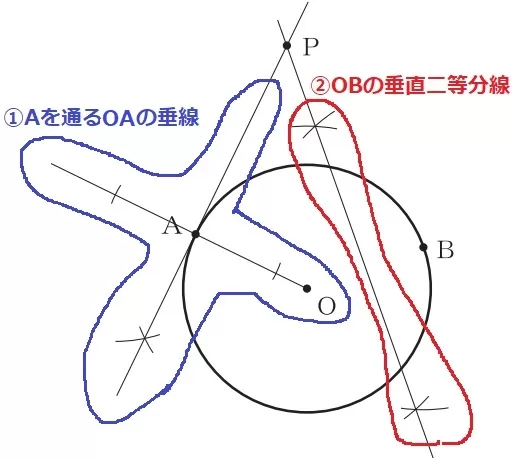
『Aを接点とする円Oの接線上』→半径OAと接線はAで直交する。
『2点O、Bから等距離にある』→OBの垂直二等分線上にある。
①Aを通るOAの垂線と②OBの垂直二等分線の交点がP。
(2) 54.8%
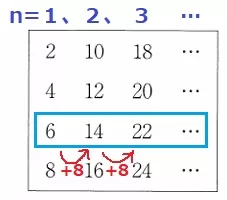
上から3番目の数列は【6、14、22、30…】
初項6、公差8の等差数列である。
8はn-1回足すので、6+8(n-1)=8n-2
*誤答では8n+6などがみられた。
@別解@
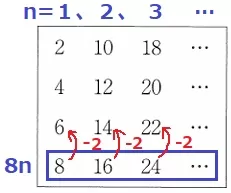
4番目がちょうど8nの数列なので、そこから-2して8n-2
(3) 75.3%
【袋A】赤3個、青2個、白1個
【袋B】赤1個、青2個
異色よりも同色の方が求めやすいので、余事象で攻める。
●赤で同色
Aの赤1、赤2、赤3とBの赤で3通り。
●青で同色
Aの青1、青2とBの青3、青4で2×2=4通り。
計7通り。全体は6×3=18通りだから、確率は1-7/18=11/18
大問3(方程式)
35.3%
何を文字に設定すべきか。
求めたいきゅうりとなすの本数をx、yに置くと、袋の数はそれぞれx/6とy/3になる。
なすは売れた(y/3-5)袋と売れ残った5袋を別で処理しなければならないので面倒くさい。
そこで、きゅうりの袋の数をx、なすの袋の数をyとする。
本数で等式。
6x+3y=360 …①
売上金額で等式。
なすは売れたy-5袋と、売れ残った5袋(4割引=60%)に分ける。
200x+140(y-5)+140×0.6×5=13000 …②
①÷3をして、2x+y=120 …③
②を整理すると、200x+140y-700+420=13000
200x+140y=13280 ←÷20
10x+7y=664 …④
④-③×5をすると、2y=64
y=32
③に代入、2x+32=120→x=44
袋の数を文字に置いたので、
きゅうりの本数は、6x=6×44=264本
なすの本数は、3y=3×32=96本
きゅうり…264本、なす…96本
大問4(空間図形)
(1) 65.7%
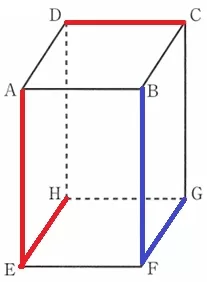
ねじれの位置→延長しても交わらない、かつ平行でもない(同一平面上にない)
CDとネジレにあるのはAE・BF・EH・FGの4本。
このうち、面BFGCと平行にあるのは辺AE、辺EH。
@@
辺BFと辺FGは面BFGC上にある。
(2) 42.0%
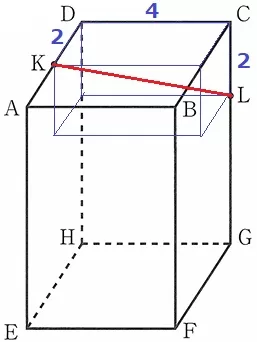
KLを対角線とする直方体をつくる。
KL=√(22+42+22)=2√6cm
*誤答では2√10が目立つ。
(3) 5.7%!!
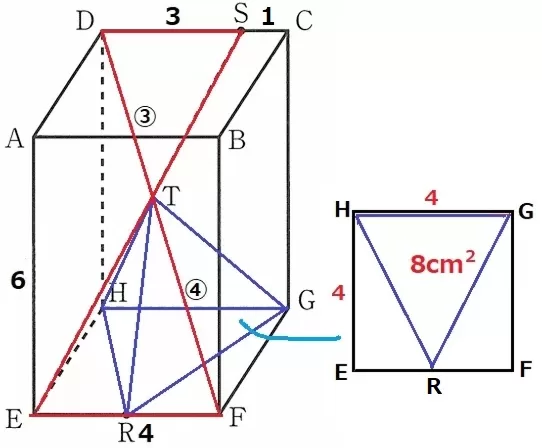
底面の△HRGの面積は、4×4÷2=8cm2
△DTS∽△FTEより、DT:TF=③:④から、
三角錐T―HRGの高さは6×④/⑦=24/7cm
三角錐の体積は、8×24/7÷3=64/7cm3
大問5(データの活用)
(1) 67.0%
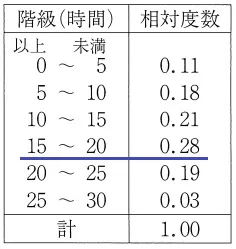
度数が最も多い階級→相対度数が最も高い15~20時間
累積相対度数…その階級以下の相対度数の合計。
〔15~20の累積相対度数=1-20~30の相対度数の合計〕
1-(0.19+0.03)=0.78
(2) 66.5%
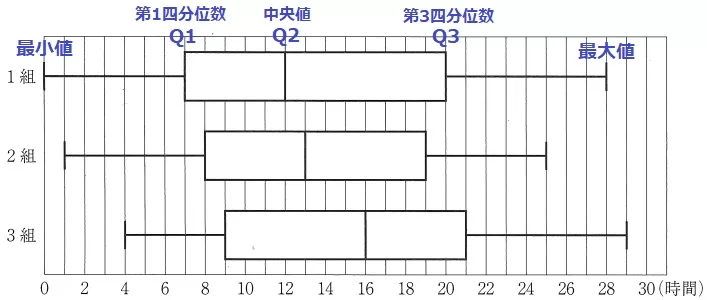
ア:範囲=最大値-最小値。1組が最も大きい。〇
イ:35人の中央値は18番目の値。Q1は下位17人の真ん中、下から9番目の値。
2組のQ1より9番目が8時間→8時間以下は少なくとも9人いる。
3組の9番目は9時間→8時間以下は多くても8人。2組の方が多い。〇
ウ:1組のQ3(上から9番目)は20時間だが、2・3組は不明。×
エ:平均値を×印で示す箱ひげ図もあるが、本問はわからない。×
ア・イ
*誤答はエが目立つ。
大問6(関数)
(1) 66.8%
反比例はxとyの積が比例定数aで一定。
A座標より、a=-6×3=-18
y=-18/x
*誤答はy=18/xなどがみられた。
(2)ア 46.8%
aの絶対値が小さいとグラフの開きは大きくなり、絶対値が大きいと開きは小さくなる。
y=ax2にA(-6、3)を代入。
3=36a
a=1/12
同様に、B(-2、9)を代入。
9=4a
a=9/4
1/12≦a≦9/4
*誤答は4a≦a≦36aや3≦a≦9などがみられた。
イ 10.8%!
答案では求める過程も書く。
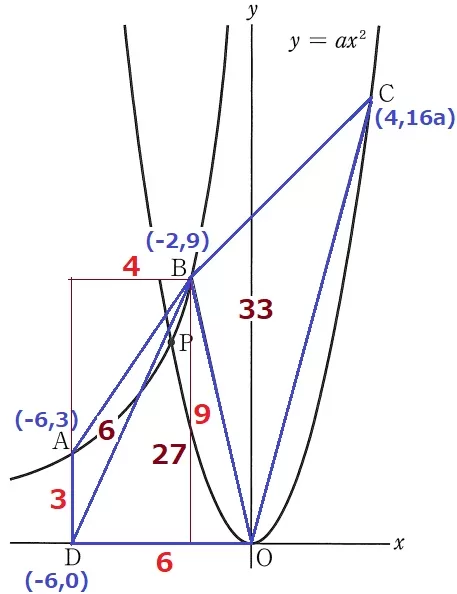
四角形ADOBをBDで分割して面積を求める。
四角形ADOB=△ADB+△BDO
=3×4÷2+6×9÷2
=33
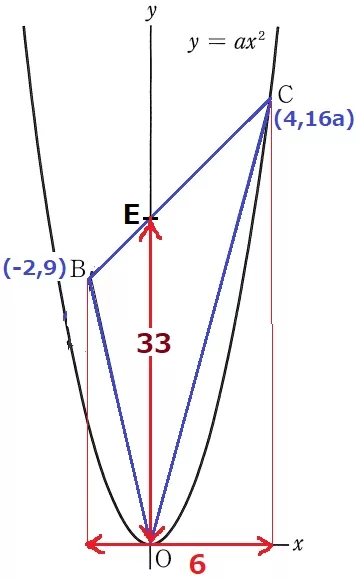
↑不要な線を消しました。BCの切片をEとする。
△BOCの面積は、6×OE÷2=33
OE=11
E(0、11)
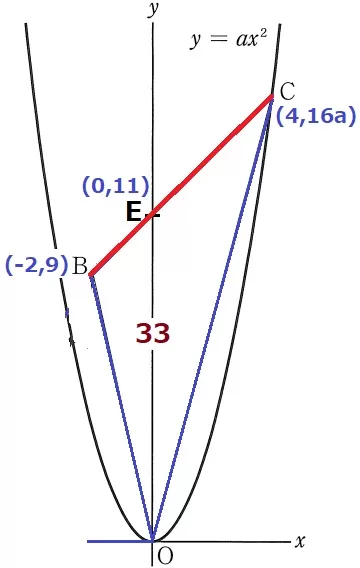
B(-2、9)→E(0、11)
右に2、上に2だから傾きは1→BE(BC);y=x+11
これにC(4、16a)を代入する。
16a=4+11
a=15/16
大問7(平面図形)
(1) 12.2%!
PA=PCの証明。
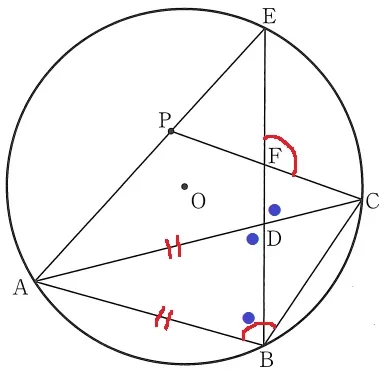
∠EFCが曲者。
仮定のAB=ADから△ABDは二等辺三角形なので、
∠ABD=∠ADB(●)とすると、対頂角から∠CDF=●
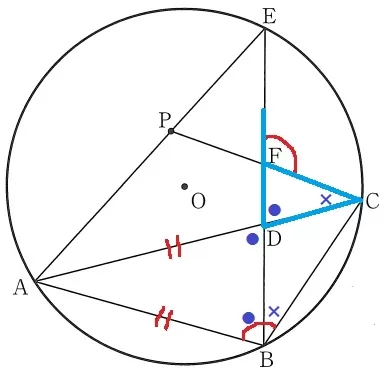
ここで、∠DCF=×とおく。
△CDFの外角定理より、●+×=∠EFC→∠EFC-●=×である。
ということは∠EFC=∠ABCなので、∠CBD=∠ABC-●=×
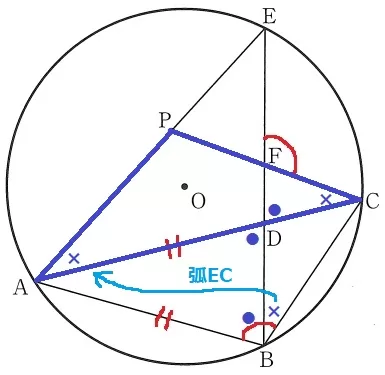
弧CEの円周角で、∠EAC=×
△PACは2つの底角が等しいから二等辺→PA=PC
@@

書き方は公式解答を参照してください。
(2) 2.6%!!
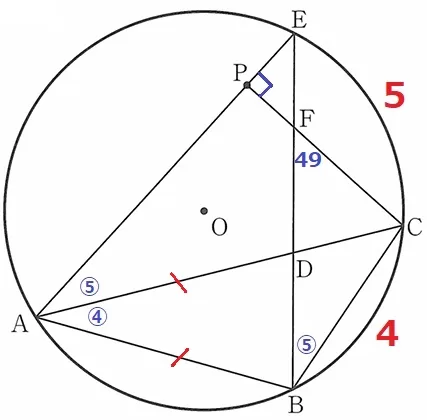
弧BC:弧CE=4:5
円周角の大きさは弧の長さに比例する。
弧BCに対する円周角∠BAC=④、
弧CEに対する円周角∠CAE=∠CBE=⑤と書いておく。
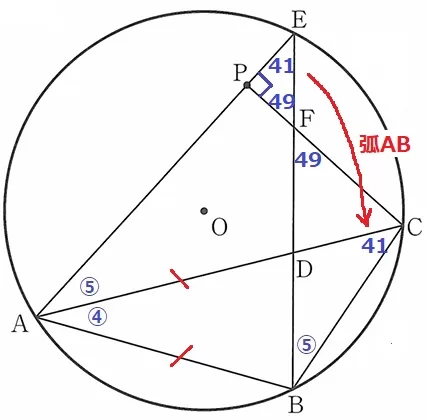
対頂角で∠EFP=49°
△EFPの内角から、∠FEP=180-(90+49)=41°
これを弧ABの円周角で移して、∠ACB=41°
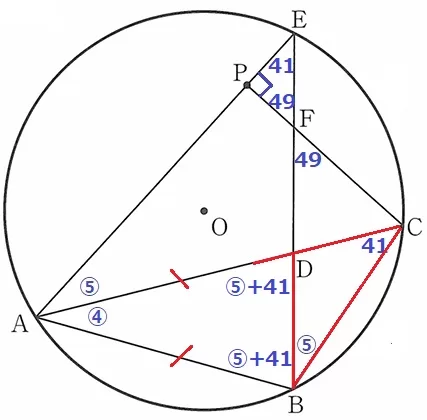
△BCDの外角定理より、∠ADB=⑤+41°
二等辺三角形ABDの内角で、④+(⑤+41)+(⑤+41)=⑭+82=180
⑭=98°
∠ADB=98×⑤/⑭+41=76°
*誤答では71などがみられる。無答も多い。
●講評●
3・6(2)イ・7(1)の記述問題は完走が難しい。
大問1
(1)エ:ルートの中身が大きい場合はa√bに変えるか、√a×√bに分解する。
大問2
(2)4行の数列なので、4行目を基準にするとnと対応させやすい。
(3)同じ色は区別する。
大問3
求めづらかったと思う。
普通は求めたいものを文字に置くが、計算のハードルが上がってしまう…。
ナスは売れた袋と売れ残った袋で値段が異なるので、袋単位で処理した方がいい。
解答までたどり着けなくても部分点はもらえる。
大問4
(1)ネジレ以外にもう1つの条件が付いていた。
(3)ラス問にしては見えやすい設問だったと思う。
高さの比で用いる△DTS∽△FTEが見やすいアングルにある。
大問5
(1)累積相対度数は〔全体-後ろの合計〕でも可。
(2)完全解答だが判断しやすかった。
大問6
(2)ア:aはPが点Aのときに最小、点Bのときに最大。
イ:頂点の座標が確定している=面積の求めやすい四角形ADOBから出発する。
底辺と高さが出しやすいBDで分割。△BOCの面積から切片E。
求めたいaはC座標にある。BE(BC)の式に座標を代入する。
大問7
(1)∠EFCの位置がビビる。
PA=PCとなるには、△PACが二等辺三角形である。
2つの底角と仮定の等角、さらに二等辺ABDの底角に印をつけると関係性が見えてくる。
(2)∠FEP=41°は必須かと思われる。
弧の長さの比から円周角の比を記し、その比と41°で3つの内角を示せる三角形を狙う。


コメント